初中数学浙教版八年级上册1.5 三角形全等的判定图文ppt课件

这是一份初中数学浙教版八年级上册1.5 三角形全等的判定图文ppt课件，共29页。PPT课件主要包含了2三条边，1三个角，3两边一角，4两角一边，SSS，两边一角，①三角，②三边，③两边一角，④两角一边等内容，欢迎下载使用。

第1章 三角形的初步认识1.5 三角形全等的判定
三角形全等的判定定理（SAS）
当两个三角形满足六个条件中的三个时，有四种情况:
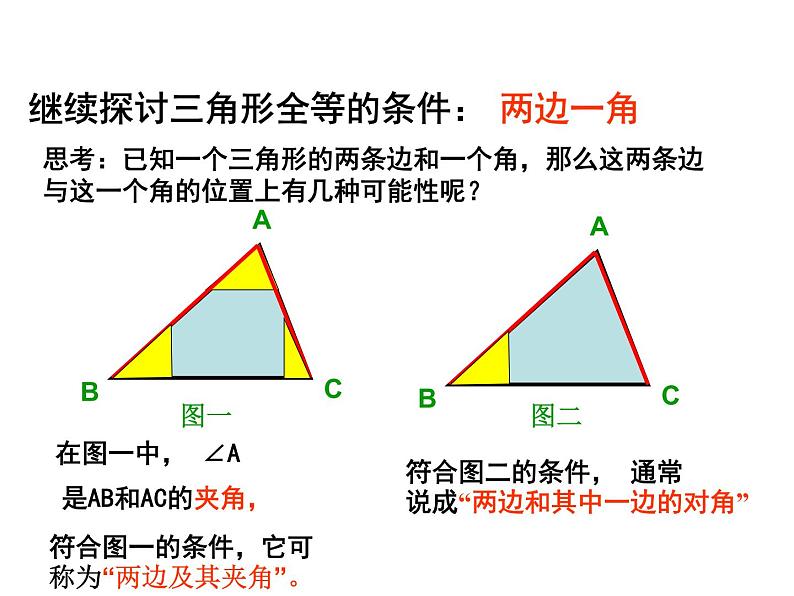
继续探讨三角形全等的条件：
思考：已知一个三角形的两条边和一个角，那么这两条边与这一个角的位置上有几种可能性呢？
符合图一的条件，它可称为“两边及其夹角”。
符合图二的条件， 通常说成“两边和其中一边的对角”
在纸上的不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm.
将这两个三角形叠在一起,它们完全重合吗？
由此你能得到什么结论？
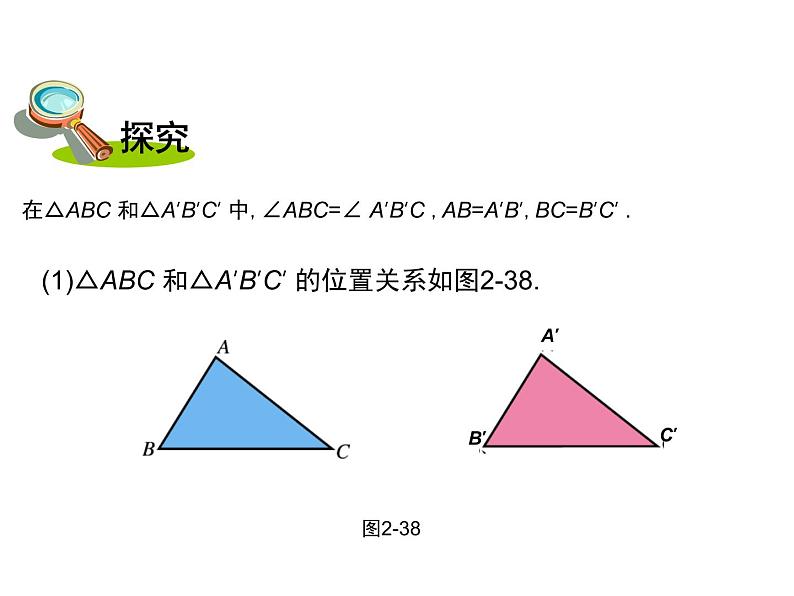
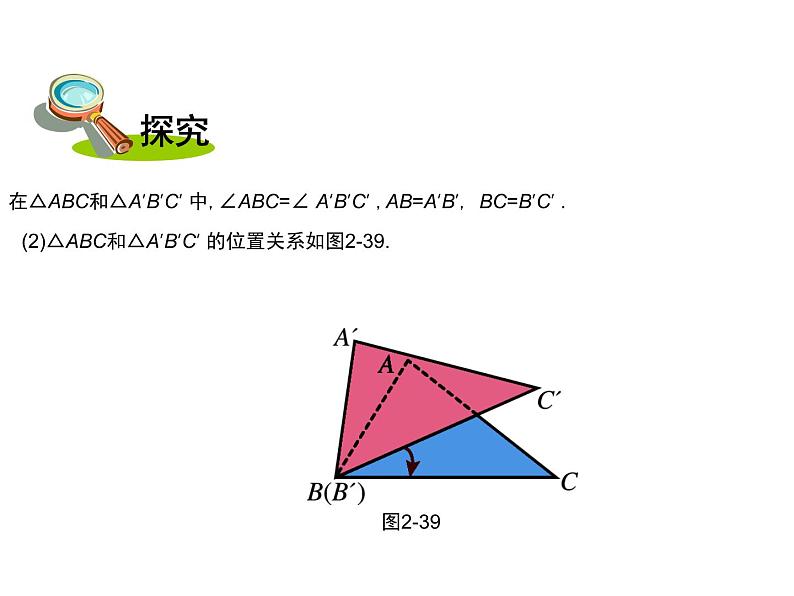
在△ABC 和△A’B’C’ 中,∠ABC=∠ A’B’C ,AB=A’B’,BC=B’C’ .
(1)△ABC 和△A’B’C’ 的位置关系如图2-38.
(2)△ABC和△A’B’C’ 的位置关系如图2-39.
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ .
(3)△ABC和△A’B’C’ 的位置关系如图2-40.
(4)△ABC和△A’B’C’ 的位置关系如图2-41.
两边及其夹角分别相等的两个三角形全等.(可简写成“边角边”或“SAS”).
S ——边 A——角
注意：两边和其中一边的对角分别相等的两个三角形 不一定全等.(即没有“边边角”或“SSA”这种判定定理).
例2 已知：如图2-42,AB和CD相交于点O,且AO=BO, CO=DO.求证：△ACO≌△BDO.
全等三角形的判定 SSS
1．掌握三角形全等的“边边边”定理．2．了解三角形的稳定性．3．经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的过程．
①AB=DE ② BC=EF ③ CA=FD ④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
1、 什么叫全等三角形？
能够重合的两个三角形叫 全等三角形。
2、 全等三角形有什么性质？
1.满足这六个条件可以保证△ABC ≌△ DEF吗？2.如果只满足这些条件中的一部分,那么能保证△ABC ≌△ DEF吗?
3.如果满足三个条件，你能说出有哪几种可能的情况？
已知两个三角形的三个内角分别为30°，60° ，90° 它们一定全等吗？
　　这说明有三个角对应相等的两个三角形不一定全等
已知两个三角形的三条边都分别为3cm、4cm、6cm 。它们一定全等吗？
问题：把你画的三角形与其他同学所画的三角形进行比较，它们能够互相重合吗？
三角形全等的条件： 三边对应相等的两个三角形全等（简写成“边边边”或“SSS”）
证明：∵BD=CE ∴ BD-ED=CE-ED， 即BE=CD。
例:如图，AB=AC，AE=AD，BD=CE，求证：△AEB ≌ △ADC
如图，已知AB=CD，AD=CB，E、F分别是AB，CD的中点，且DE=BF.
求证：①△ADE≌△CBF,②∠A=∠C
∴△ADE≌△CBF∴∠A=∠C
两边分别相等且其一组等边的对角相等的两个三角形不一定全等
两角一对边(AAS)?
1．掌握三角形全等的“角角边”定理．2．能根据条件选择合适的判定进行推理论证。
△ABC与△DEF中，AB=DE, ∠A= ∠D, ∠C= ∠F.
角角边公理:两角分别相等及其中一组等角的对边也相等的两个三角形全等.(AAS)