

初中数学第4章 锐角三角函数综合与测试课后复习题
展开满分120分
姓名:___________班级:___________学号:___________
一.选择题(共12小题,满分36分,每小题3分)
1.在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A.B.C.D.
2.已知sinA=0.9816,运用科学计算器求锐角A时(在开机状态下),按下的第一个键是( )
A.B.C.D.
3.如图,在△ABC中,∠ACB=90°,D是AB的中点,若CD=5,AC=8,则tanA=( )
A.B.C.D.
4.如图,有一斜坡AB的长AB=10米,坡角∠B=36°,则斜坡AB的铅垂高度AC为( )
A.10tan36°B.10cs36°C.10sin36°D.
5.已知csα=,则锐角α的取值范围是( )
A.0°<α<30°B.30°<α<45°C.45°<α<60°D.60°<α<90°
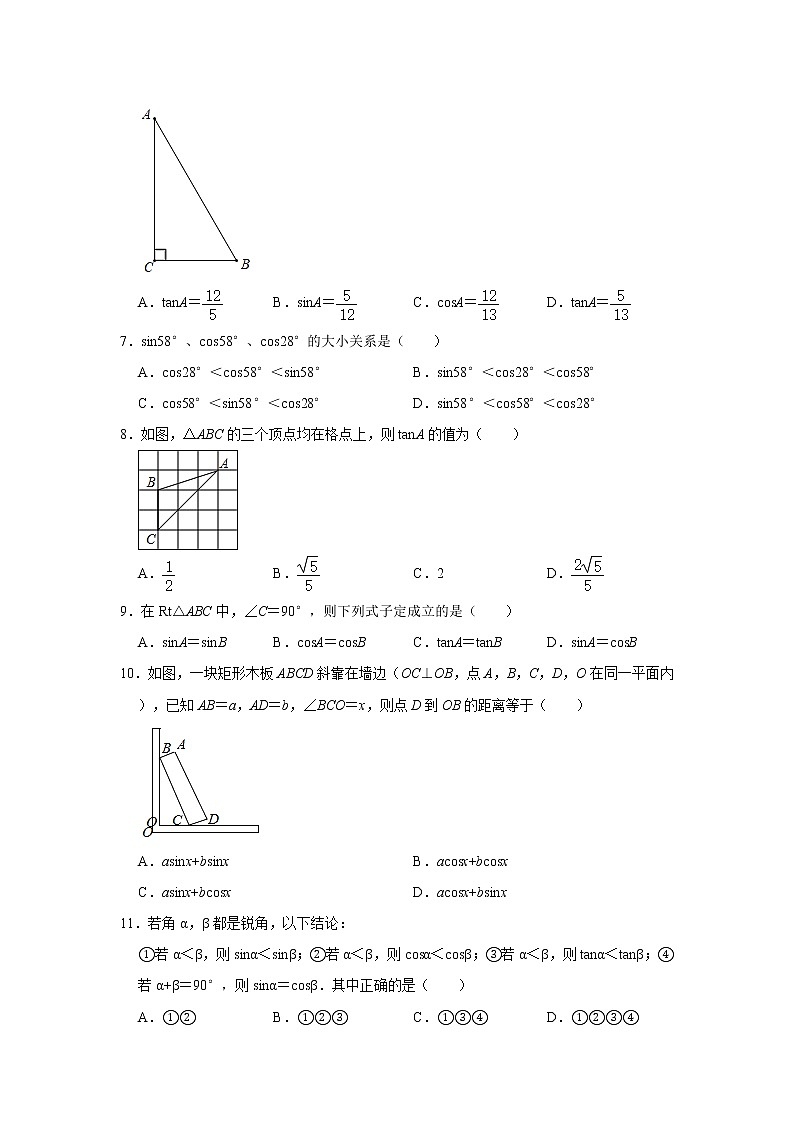
6.在Rt△ABC中,∠C=90°,BC:AB=5:13,则下列等式正确的是( )
A.tanA=B.sinA=C.csA=D.tanA=
7.sin58°、cs58°、cs28°的大小关系是( )
A.cs28°<cs58°<sin58°B.sin58°<cs28°<cs58°
C.cs58°<sin58°<cs28°D.sin58°<cs58°<cs28°
8.如图,△ABC的三个顶点均在格点上,则tanA的值为( )
A.B.C.2D.
9.在Rt△ABC中,∠C=90°,则下列式子定成立的是( )
A.sinA=sinBB.csA=csBC.tanA=tanBD.sinA=csB
10.如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内),已知AB=a,AD=b,∠BCO=x,则点D到OB的距离等于( )
A.asinx+bsinxB.acsx+bcsx
C.asinx+bcsxD.acsx+bsinx
11.若角α,β都是锐角,以下结论:
①若α<β,则sinα<sinβ;②若α<β,则csα<csβ;③若α<β,则tanα<tanβ;④若α+β=90°,则sinα=csβ.其中正确的是( )
A.①②B.①②③C.①③④D.①②③④
12.我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东60°方向走到B地,再沿北偏西37°方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为( )(参考数据sin53°≈0.80,cs53°≈0.60,tan53°≈1.32)
A.12千米B.(3+4)千米
C.(3+5)千米D.(12﹣4)千米
二.填空题(共6小题,满分24分,每小题4分)
13.已知tan(α+15°)=,则锐角α的度数为 °.
14.比较大小:sin81° tan47°(填“<”、“=”或“>”).
15.如图,在△ABC中,∠C=90°,AC=6,若csA=,则BC的长为 .
16.如图所示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是 .
17.小致为了测量楼房AB的高度,他从楼底的B处沿着斜坡行走20m,达到坡顶D处.已知斜坡的坡角为15°,小致的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,则楼房AB的高度为 m.(计算结果精确到1m,参考数据:sin15°=,cs15°=,tan15°=.)
18.如图,BE是△ABC的角平分线,F是AB上一点,∠ACF=∠EBC,BE、CF相交于点G.若sin∠AEB=,BG=4,EG=5,则S△ABE= .
三.解答题(共7小题,满分60分)
19.(12分)计算:
(1)2sin30°+3cs60°﹣4tan45°
(2)+tan260°
20.(6分)如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
21.(6分)在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.若a=2,sin,求b和c.
22.(8分)2019年4月18日,台湾省花莲县发生里氏6.7级地震,救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距6米,探测线与地面的夹角分别为30°和60°,如图所示,试确定生命所在点C的深度.(结果精确到0.1米,参考数据≈1.41,≈1.73)
23.(9分)嘉琪在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,sin222°+sin268°≈0.372+0.932=1.0018,sin229°+sin261°≈0.482+0.872=0.9873,sin237°+sin253°≈0.602+0.802=1.0000,sin245°+sin245°=()2+()2=1.
据此,嘉琪猜想:在Rt△ABC中,∠C=90°,设∠A=α,有sin2α+sin2(90°﹣α)=1.
(1)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立.
(2)请你对嘉琪的猜想进行证明.
24.(9分)如图,小明利用学到的数学知识测量大桥主架在水面以上的高度AB,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离CM为60米,且AB垂直于桥面.(点A,B,C,M在同一平面内)
(1)求大桥主架在桥面以上的高度AM;(结果保留根号)
(2)求大桥主架在水面以上的高度AB.(结果精确到1米)
(参考数据sin14°≈0.24,cs14°≈0.97,tan14°≈0.25,≈1.73)
25.(10分)已知△ABC,AB=AC,∠BAC=90°,D是AB边上一点,连接CD,E是CD上一点,且∠AED=45°.
(1)如图1,若AE=DE,
①求证:CD平分∠ACB;
②求的值;
(2)如图2,连接BE,若AE⊥BE,求tan∠ABE的值.
参考答案
一.选择题(共12小题,满分36分,每小题3分)
1.解:如图所示:
∵∠C=90°,BC=5,AC=12,
∴AB==13,
∴sinB==.
故选:D.
2.解:∵已知sinA=0.9816,运用科学计算器求锐角A时(在开机状态下)的按键顺序是:2ndF,sin,0,
∴按下的第一个键是2ndF.
故选:D.
3.解:∵∠ACB=90°,D是AB的中点,CD=5,
∴AB=2CD=10,
∵AC=8,AB=10,
∴BC==6,
∴tanA===.
故选:C.
4.解:在Rt△ABC中,sinB=,
∴AC=AB•sinB=10sin36°,
故选:C.
5.解:∵cs30°=,cs45°=,
∵<<,
∴30°<α<45°,
故选:B.
6.解:设BC=5x,则AB=13x,
由勾股定理得,AC==12x,
则tanA==,A、D错误;
sinA==,B错误;
csA==,C正确;
故选:C.
7.解:sin58°=cs32°.
∵58°>32°>28°,
∴cs58°<cs32°<cs28°,
∴cs58°<sin58°<cs28°.
故选:C.
8.解:如图所示:连接BD,
BD==,
AD==2,
AB==,
∵BD2+AD2=2+8=10=AB2,
∴△ADB为直角三角形,
∴∠ADB=90°,
则tanA===.
故选:A.
9.解:∵∠C=90°,
∴∠A+∠B=90°,
∴sinA=csB.
故选:D.
10.解:如图,过点D作DE⊥OC于点E,
则点D到OB的距离等于OE的长.
∵四边形ABCD是矩形,
∴∠BCD=90°,CD=AB=a,AD=BC=b,
∴∠CDE=∠BCO=x,
∴OC=BC•csx=bcsx,
CE=CD•sinx=asinx,
∴OE=OC+CE=bcsx+asinx.
则点D到OB的距离等于bcsx+asinx.
故选:C.
11.解:①∵sinα随α的增大而增大,∴若α<β,则sinα<sinβ,此结论正确;
②∵csα随α的增大而减小,∴若α<β,则csα>csβ,此结论错误;
③∵tanα随α的增大而增大,∴若α<β,则tanα<tanβ,此结论正确;
④若α+β=90°,则sinα=csβ,此结论正确;
综上,正确的结论为①③④,
故选:C.
12.解:如图,作BD⊥AC于点D,
根据题意可知:
在Rt△ADB中,∠A=60°,AB=6,
∴AD=3,BD=3,
在Rt△CDB中,∠CBD=53°,
∴CD=BD•tan53°≈3×1.32≈3×≈4,
∴AC=AD+CD=3+4.
则A,C两地的距离为(3+4)千米.
故选:B.
二.填空题(共6小题,满分24分,每小题4分)
13.解:∵tan30°=,
∴α+15°=30°,
∴α=15°,
故答案为:15.
14.解:∵sin81°<sin90°=1,tan47°>tan45°=1,
∴sin81°<1<tan47°,
∴sin81°<tan47°.
故答案为<.
15.解:∵在△ABC中,∠C=90°,AC=6,csA=,
∴csA===,
∴AB=10,
∴BC====8.
故答案为:8.
16.解:如图,连接AB.
∵OA=AB=,OB=2,
∴OB2=OA2+AB2,
∴∠OAB=90°,
∴△AOB是等腰直角三角形,
∴∠AOB=45°,
∴sin∠AOB=,
故答案为:.
17.解:作DH⊥AB于H,
∵∠DBC=15°,BD=20m,
∴BC=BD•cs∠DBC=20×=19.2(m),CD=BD•sin∠DBC=20×=5(m),
由题意得,四边形ECBF和四边形CDHB是矩形,
∴EF=BC=19.2m,BH=CD=5m,
∵∠AEF=45°,
∴AF=EF=19.2m,
∴AB=AF+FH+HB=19.2+1.6+5=25.8≈26(m),
答:楼房AB的高度约为26m.
故答案是:26.
18.解:如图,过点B作BT⊥AC于T,连接EF.
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠ECG=∠ABE,
∴∠ECG=∠CBE,
∵∠CEG=∠CEB,
∴△ECG∽△EBC,
∴==,
∴EC2=EG•EB=5×(5+4)=45,
∵EC>0,
∴EC=3,
在Rt△BET中,∵sin∠AEB==,BE=9,
∴BT=,
∴ET===,
∴CT=ET+CE=,
∴BC===6,
∴CG==10,
∵∠ECG=∠FBG,
∴E,F,B,C四点共圆,
∴∠EFG=∠CBG,
∵∠FGE=∠BGC,
∴△EGF∽△CGB,
∴=,
∴=,
∴EF=3,
∵∠AFE=∠ACB,∠EAF=∠BAC,
∴△EAF∽△BAC,
∴===,设AE=x,则AB=2x,
∵∠FBG=∠ECG,∠BGF=∠CGE,
∴△BGF∽△CGE,
∴=,
∴=,
∴BF=,
∵AE•AC=AF•AB,
∴x(x+3)=(2x﹣)•2x,
解得x=,
∴AE=ET=,
∴点A与点T重合,
∴AB=2AE=,
∴S△ABE=×AB×AE=××=.
故答案为.
三.解答题(共7小题,满分60分)
19.解:(1)原式=
=
=;
(2)原式=
=+3
=.
20.解:过点A作AH⊥BC于H,
∵S△ABC=27,
∴,
∴AH=6,
∵AB=10,
∴BH===8,
∴tanB===.
21.解:如图,
∵a=2,sin,
∴c===6,
则b===4.
22.解:过点C作CD⊥AB,交AB 的延长线于D,
在Rt△ACD中,∠CAD=30°,tan∠CAD=,
∴AD==CD,
在Rt△ACD中,∠CBD=60°,tan∠CBD=,
∴BD==CD,
由题意得,AD﹣BD=AB=6,
∴CD﹣CD=6,
解得,CD=3≈5.2(米),
答:生命所在点C的深度约为5.2米.
23.解:(1)当α=30°时,
sin2α+sin2(90°﹣α)
=sin230°+sin260°
=()2+()2
=+
=1;
(2)嘉琪的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=()2+()2
=
=
=1.
24.解:(1)∵AB垂直于桥面,
∴∠AMC=∠BMC=90°,
在Rt△AMC中,CM=60,∠ACM=30°,
tan∠ACM=,
∴AM=CM•tan∠ACM=60×=20(米),
答:大桥主架在桥面以上的高度AM为20米;
(2)在Rt△BMC中,CM=60,∠BCM=14°,
tan∠BCM=,
∴MB=CM•tan∠BCM≈60×0.25=15,
∴AB=AM+MB=15+20≈50(米)
答:大桥主架在水面以上的高度AB约为50米.
25.(1)①证明:∵AE=DE,
∴∠ADE=∠DAE,
∵∠CAD=90°,
∴∠ADC+∠ACD=90°,∠DAE+∠CAE=90°,
∴∠CAE=∠ACD,
∴EA=EC,
∵∠AED=45°=∠CAE+∠ACD,
∴∠ACD=22.5°,
∵AB=AC,∠BAC=90°,
∴∠ACB=45°,
∴∠BCD=∠ACD=22.5°,
∴CD平分∠ACB.
②解:如图1中,过点D作DT⊥BC于T.
∵CD平分∠ACB,DT⊥CB,DA⊥CA,
∴DA=DT,
∵AB=AC,∠BAC=90°,
∴∠B=45°,
∴BD=DT=AD,
∴=.
(2)解:如图2中,连接BE,过点C作CT⊥AT交AE的延长线于T.
∵AE⊥BE,CT⊥AT,
∴∠AEB=∠T=∠BAC=90°,
∴∠BAE+∠ABE=90°,∠BAE+∠CAE=90°,
∴∠ABE=∠CAT,
∵AB=AC,
∴△ABE≌△CAT(AAS),
∴AE=CT,BE=AT,
∵∠AED=∠CET=45°,∠T=90°,
∴ET=CT=AE,
∴BE=2AE,
∴tan∠ABE==
题号
一
二
三
总分
得分
湘教版九年级上册第4章 锐角三角函数综合与测试课后复习题: 这是一份湘教版九年级上册第4章 锐角三角函数综合与测试课后复习题,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学1.锐角三角函数课后作业题: 这是一份初中数学1.锐角三角函数课后作业题,文件包含第15讲锐角三角函数九年级数学精品课程华师大版解析版doc、第15讲锐角三角函数九年级数学精品课程华师大版原卷版doc等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
初中数学湘教版九年级上册第4章 锐角三角函数综合与测试课时练习: 这是一份初中数学湘教版九年级上册第4章 锐角三角函数综合与测试课时练习,共9页。试卷主要包含了下面四个数中,最大的是等内容,欢迎下载使用。













