湘教版数学九上 3.4.2 相似三角形的性质 第2课时 课件

这是一份湘教版数学九上 3.4.2 相似三角形的性质 第2课时 课件，共14页。

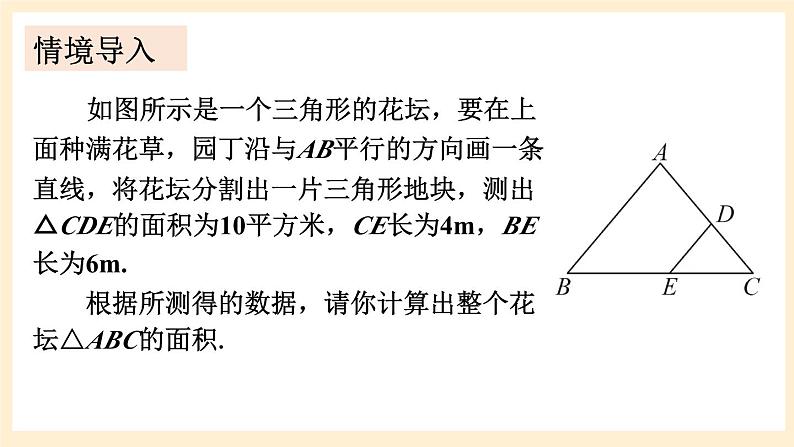
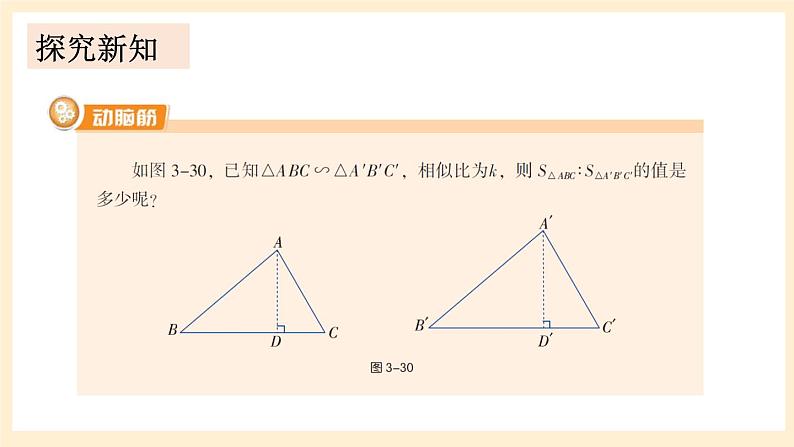
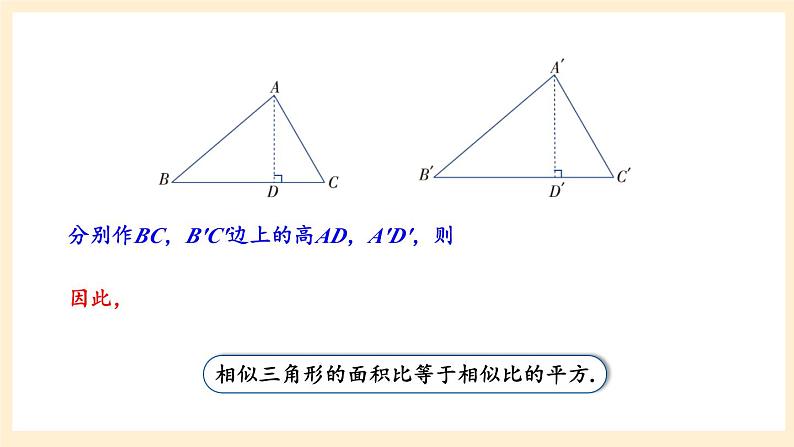
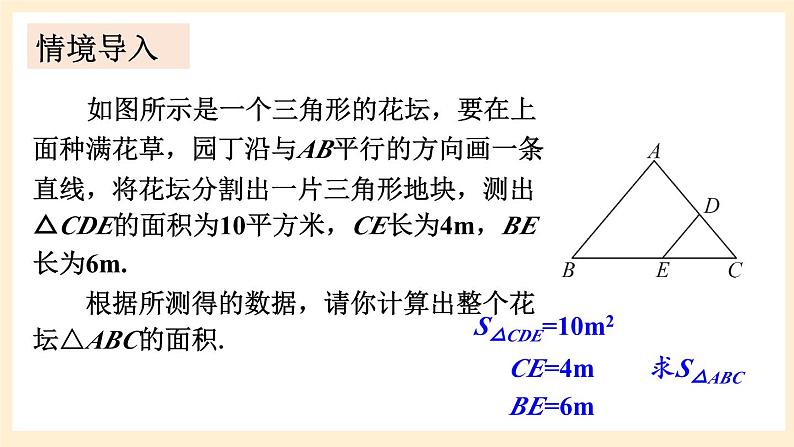
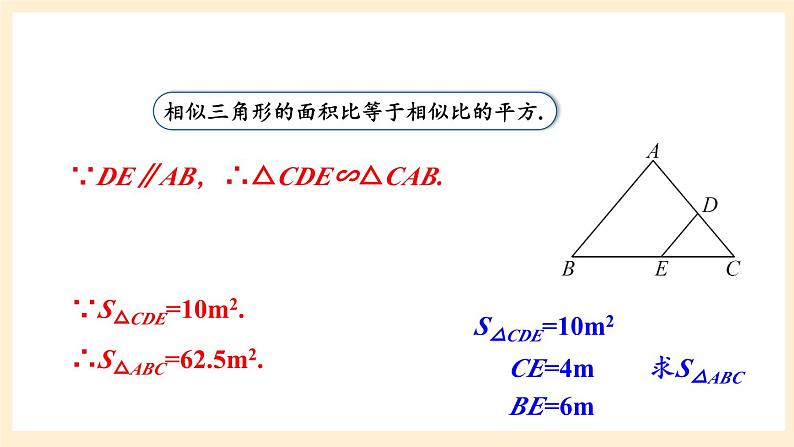
湘教版数学九年级上册3.4.2.2与相似三角形的周长、面积有关的性质情境导入 如图所示是一个三角形的花坛，要在上面种满花草，园丁沿与AB平行的方向画一条直线，将花坛分割出一片三角形地块，测出△CDE的面积为10平方米，CE长为4m，BE长为6m. 根据所测得的数据，请你计算出整个花坛△ABC的面积. 情境导入探究新知分别作BC，B′C′边上的高AD，A′D′，则因此， 如图所示是一个三角形的花坛，要在上面种满花草，园丁沿与AB平行的方向画一条直线，将花坛分割出一片三角形地块，测出△CDE的面积为10平方米，CE长为4m，BE长为6m. 根据所测得的数据，请你计算出整个花坛△ABC的面积. S△CDE=10m2CE=4mBE=6m求S△ABC 情境导入S△CDE=10m2CE=4mBE=6m求S△ABC∴S△ABC=62.5m2.∵S△CDE=10m2.∵DE∥AB，∴△CDE∽△CAB.例11如图，在△ABC中，EF∥BC， ，S四边形BCFE=8，求S△ABC.解：∵EF∥BC，∴△AEF∽△ABC.∵S四边形BCFE=8，∴S△AEF=1.∴S△ABC=9.例12 已知△ABC与△A′B′C′的相似比为 ，且S△ABC+S△A′B′C′=91，求△A′B′C′的面积.解：∵ △ABC与△A′B′C′的相似比为 ， 又 S△ABC+ S△A′B′C′ =91，∴S△A′B′C′ =63.练习1.证明：相似三角形的周长比等于相似比.ABCA′B′C′课堂练习ABCA′B′C′证明：∵△A′B′C′∽△ABC，其相似比为k，∴C△ABC=AB+AC+BC=k(A′B′+A′C′+B′C′).∵C△A′B′C′= A′B′+A′C′+B′C′，2.已知△ABC∽△ A′B′C′，它们的周长分别为60cm和72cm，且AB=15cm，B′C′=24cm，求BC，AC， A′B′， A′C′的长.ABCA′B′C′解：∵△ABC∽△A′B′C′ ，∵ AB=15cm，B′C′=24cm，∴ A′B′=18cm，BC=20cm.∵C△ABC=60， C△A′B′C′ =72，∴ AC=25cm，A′C′=30cm.3.有一个直角三角形的边长分别为3,4,5，另一个与它相似的直角三角形的最小边长为7，则另一个直角三角形的周长和面积分别是多少？ABCA′B′C′解：∵Rt△A′B′C′∽Rt△ABC，∵C△ABC=12，∴C△A′B′C′ =28.∵S△ABC=6，课堂小结1.从课后习题中选取；2.完成练习册本课时的习题.课后作业