




- 22.1.4《二次函数y=ax²+bx+c的图像和性质》PPT课件 课件 16 次下载
- 22.2《 二次函数与一元二次方程》PPT课件 课件 14 次下载
- 23.1《 图形的旋转》PPT课件 课件 16 次下载
- 23.2.1《中心对称》PPT课件 课件 10 次下载
- 23.2.2《中心对称图形》PPT课件 课件 12 次下载
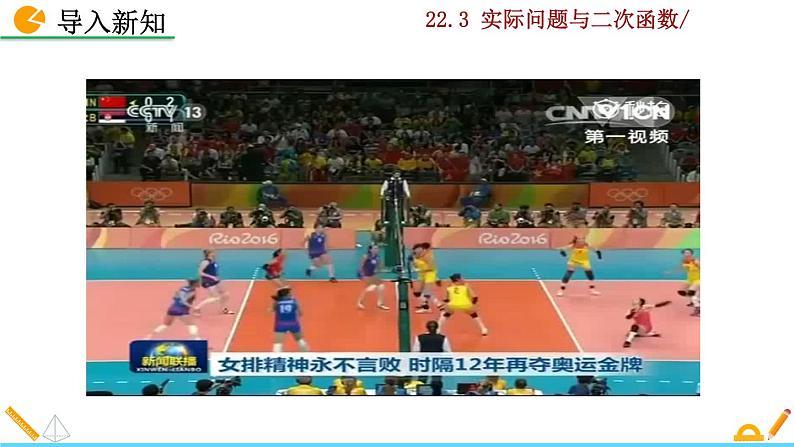
初中数学人教版九年级上册第二十二章 二次函数22.3 实际问题与二次函数精品课件ppt
展开排球运动员从地面竖直向上抛出排球,排球的高度 h(单位:m)与排球的运动时间 t(单位:s)之间的关系式是h= 20t - 5t 2 (0≤t≤4).排球的运动时间是多少时,排球最高?排球运动中的最大高度是多少?
2.会应用二次函数的性质解决实际问题.
1. 掌握几何问题中的相等关系的寻找方法,并会应用函数关系式求图形面积的最值.
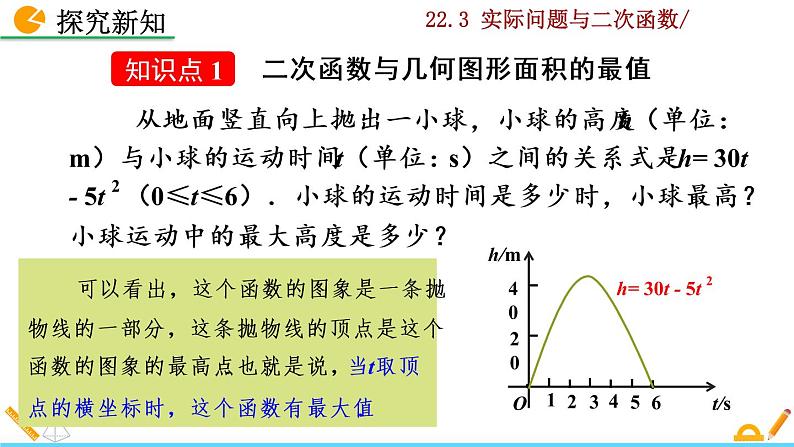
从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球的运动时间 t(单位:s)之间的关系式是 h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小球最高?小球运动中的最大高度是多少?
二次函数与几何图形面积的最值
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是这个函数的图象的最高点.也就是说,当t取顶点的横坐标时,这个函数有最大值.
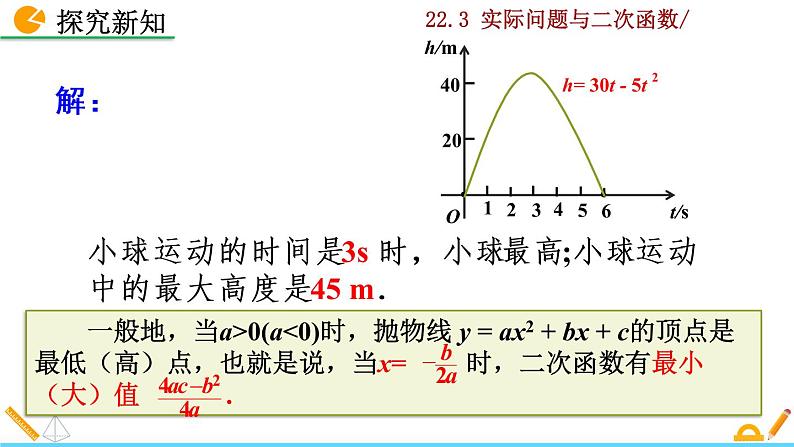
【想一想】如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
小球运动的时间是 3s 时,小球最高;小球运动中的最大高度是 45 m.
例1 用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
问题1 矩形面积公式是什么?
问题2 如何用l表示另一边?
问题3 面积S的函数关系式是什么?
利用二次函数求几何图形的面积的最值
用总长为60m的篱笆围城一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
即当l是15m时,场地的面积S最大.
矩形场地的周长是60m,一边长为lm,
所以另一边长为 m.
因此,当 时,
利用二次函数解决几何图形中的最值问题的要点:1.根据面积公式、周长公式、勾股定理等建立函数关系式;2.确定自变量的取值范围;3.根据开口方向、顶点坐标和自变量的取值范围画草图;4.根据草图求所得函数在自变量的允许范围内的最大值或最小值.
变式1 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长32m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
问题2 我们可以设面积为S,如何设自变量?
问题3 面积S的函数关系式是什么?
问题1 变式1与例题有什么不同?
S=x(60-2x)=-2x2+60x.
设垂直于墙的边长为x米
问题4 如何求解自变量x的取值范围?墙长32m对此题有什么作用?
问题5 如何求最值?
最值在其顶点处,即当x=15m时,S=450m2.
0<60-2x≤32,即14≤x<30.
变式2 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
问题1 变式2与变式1有什么异同?
问题2 可否模仿变式1设未知数、列函数关系式?
问题3 可否试设与墙平行的一边为x米?则如何表示另一边与面积?
答案:设矩形面积为Sm2,与墙平行的一边为x米,则
问题4 当x=30时,S取最大值,此结论是否正确?
问题5 如何求自变量的取值范围?
问题6 如何求最值?
由于30 >18,因此只能利用函数的增减性求其最值.当x=18时,S有最大值是378.
实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量的取值范围.通过变式1与变式2的对比,希望同学们能够理解函数图象的顶点、端点与最值的关系,以及何时取顶点处、何时取端点处才有符合实际的最值.
已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?
解:∵直角三角形两直角边之和为8,设一边长x∴ 另一边长为8-x. 则该直角三角形面积:即:当S有最大值 =∴当 时,直角三角形面积最大,最大值为8.
x= =4,另一边为4时
如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏. (1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
解:设AB=xm,则BC=(100﹣2x)m,根据题意得x(100﹣2x)=450,解得x1=5,x2=45;当x=5时,100﹣2x=90>20,不合题意舍去;当x=45时,100﹣2x=10,答:AD的长为10m;
解:设AD=xm,∴S= x(100﹣x)=﹣(x﹣50)2+1250,当a≥50时,则x=50时,S的最大值为1250;当0<a<50时,则当0<x≤a时,S随x的增大而增大;当x=a时,S的最大值为50a﹣a2,综上所述,当a≥50时,S的最大值为1250;当0<a<50时,S的最大值为50a﹣ a2.
(2)求矩形菜园ABCD面积的最大值.
1. 用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为18m,这个矩形菜园的最大面积是________.
2.如图1,在△ABC中, ∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿AB向B以2cm/s的速度移动(不与点B重合),动点Q从点B开始BC以4cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过 秒,四边形APQC的面积最小.
1. 如图,点E、F、G、H分别位于正方形ABCD的四条边上,四边形EFGH也是正方形,当点E位于何处时,正方形EFGH的面积最小?
解:令AB长为1,设DH=x,正方形EFGH的面积为y,则DG=1-x.即当E位于AB中点时,正方形EFGH面积最小.
2. 某小区在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙, 另三边用总长为40m的栅栏围住.设绿化带的边长BC为xm,绿化带的面积为ym².(1)求y与x之间的函数关系式,并写出自变量的取值范围.
(2)当x为何值时,满足条件的绿化带的面积最大?
某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2). (1)写出S与x之间的关系式,并写出自变量x的取值范围;
解:(1)设矩形一边长为x,则另一边长为(6-x),
S=x(6-x)=-x2+6x,其中0<x<6.
(2)S=-x2+6x=-(x-3)2+9;
当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元)
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
常见几何图形的面积公式
最值有时不在顶点处,则要利用函数的增减性来确定
在日常生活中存在着许许多多的与数学知识有关的实际问题。如繁华的商业城中很多人在买卖东西。
【思考】如果你去买商品,你会选买哪一家呢?如果你是商场经理,如何定价才能使商场获得最大利润呢?
2. 弄清商品销售问题中的数量关系及确定自变量的取值范围.
1. 能应用二次函数的性质解决商品销售过程中的最大利润问题.
某商品现在的售价为每件60元,每星期可卖出300件,已知商品的进价为每件40元,则每星期销售额是 元,销售利润 元.
(1)销售额= 售价×销售量;
(2)利润= 销售额-总成本=单件利润×销售量;
(3)单件利润=售价-进价.
例1 某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
涨价销售①每件涨价x元,则每星期售出商品的利润y元,填空:
y=(20+x)(300-10x)
建立函数关系式:y=(20+x)(300-10x),
即:y=-10x2+100x+6000.
②自变量x的取值范围如何确定?
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故300-10x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤30.
③涨价多少元时,利润最大,最大利润是多少?
y=-10x2+100x+6000,
即定价65元时,最大利润是6250元.
降价销售①每件降价x元,则每星期售出商品的利润y元,填空:
y=(20-x)(300+18x)
建立函数关系式:y=(20-x)(300+18x),
即y=-18x2+60x+6000.
综合可知,应定价65元时,才能使利润最大.
②自变量x的取值范围如何确定?
营销规律是价格下降,销量上升,因此只要考虑单件利润就可以,故20-x ≥0,且x ≥0,因此自变量的取值范围是0 ≤x ≤20.
③涨价多少元时,利润最大,是多少?
即定价57.5元时,最大利润是6050元.
即:y=-18x2+60x+6000,
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗?
例2 某网络玩具店引进一批进价为20元/件的玩具,如果以单价30元出售,那么一个月内售出180件,根据销售经验,提高销售单价会导致销售量的下降,即销售单价每上涨1元,月销售量将相应减少10件,当销售单价为多少元时,该店能在一个月内获得最大利润?
①每件商品的销售单价上涨x元,一个月内获取的商品总利润为y元,填空:
y=(10+x)(180-10x)
建立函数关系式:y=(10+x)(180-10x),
即:y=-10x2+80x+1800.
营销规律是价格上涨,销量下降,因此只要考虑销售量就可以,故180-10x ≥0,因此自变量的取值范围是x ≤18.
y=-10x2+80x+1800 =-10(x-4)2+1960.
当x=4时,即销售单价为34元时,y取最大值1960元.
答:当销售单价为34元时,该店在一个月内能获得最大利润1960元.
求解最大利润问题的一般步骤
(1)建立利润与价格之间的函数关系式:运用“总利润=总售价-总成本”或“总利润=单件利润×销售量”
(2)结合实际意义,确定自变量的取值范围;
(3)在自变量的取值范围内确定最大利润: 可以利用配方法或公式法求出最大利润;也可以画出函数的简图,利用简图和性质求出.
某商店购进一批单价为20元的日用品,如果以单价30元销售,那么半个月内可以售出400件.根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价提高多少元时,才能在半个月内获得最大利润?
解:设售价提高x元时,半月内获得的利润为y元.则 y=(x+30-20)(400-20x) =-20x2+200x+4000 =-20(x-5)2+4500 ∴当x=5时,y最大 =4500 答:当售价提高5元时,半月内可获最大利润4500元.
例3 某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在40~50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
解:由题意得:当40≤x≤50时, Q = 60(x-30)= 60x-1800 ∵ y = 60 > 0,Q随x的增大而增大 ∴当x最大= 50时,Q最大= 1200 答:此时每月的总利润最多是1200元.
限定取值范围中如何确定最大利润
(2)当售价在50~70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:当50≤x≤70时, 设y与x函数关系式为y=kx+b, ∵线段过(50,60)和(70,20).
50k+b=6070k+b=20
∴ y =-2x +160(50≤x≤70)
k =-2b = 160
∴Q=(x-30)y =(x-30)(-2x + 160) =-2x2 + 220x- 4800 =-2(x-55)2 +1250 (50≤x≤70) ∵a = -2<0,图象开口向下,∴当x = 55时,Q最大= 1250∴当售价在50~70元时,售价x是55元时,获利最大, 最大利润是1250元.
解:∵当40≤x≤50时, Q最大= 1200<1218 当50≤x≤70时, Q最大= 1250>1218 ∴售价x应在50~70元之间. 因此令:-2(x-55)2 +1250=1218 解得:x1=51,x2=59 当x1=51时,y1=-2x+160=-2×51+160= 58(件) 当x2=59时,y2=-2x+160= -2×59+160= 42(件)∴若4月份该商品销售后的总利润为1218元,则该商品售价为51元或59元,当月的销售量分别为58件或42件.
(3)若4月份该商品销售后的总利润为1218元,则该商品售价与当月的销售量各是多少?
变式:(1)若该商品售价在40~70元之间变化,根据例题的分析、解答,直接写出每月总利润Q与售价x的函数关系式;并说明,当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
解:Q与x的函数关系式为:
60x-1800 (40≤x≤50 )-2(x-55)2 + 1250 (50≤x≤70)
由例3可知:若40≤x≤50, 则当x=50时,Q最大= 1200若50≤x≤70, 则当x=55时,Q最大= 1250∵1200<1250∴售价x是55元时,获利最大,最大利润是1250元.
(2)若该商店销售该商品所获利润不低于1218元,试确定该商品的售价x的取值范围;
解:①当40≤x≤50时,∵Q最大= 1200<1218, ∴此情况不存在.
②当50≤x≤70时, Q最大= 1250>1218, 令Q = 1218,得 -2(x-55)2 +1250=1218 解得:x1=51,x2=59 由Q = -2(x-55)2 +1250的图象和性质可知: 当51≤x≤59时,Q≥1218因此若该商品所获利润不低于1218元,则售价x的取值范围为51≤x≤59.
(3)在(2)的条件下,已知该商店采购这种新商品的进货款不低于1620元,则售价x为多少元时,利润最大,最大利润是多少元?
51≤x≤5930 (-2 x +160)≥1620
解得:51≤x≤53
∵Q=-2(x-55)2 +1250的顶点 不在51≤x≤53范围内,又∵a =-2<0,∴当51≤x≤53时 ,Q随x的增大而增大∴当x最大 = 53时,Q最大= 1242∴此时售价x应定为53元,利润最大,最大利润是1242元.
某商店购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,据销售经验,售价每提高1元,销售量相应减少10个. (1)假设销售单价提高x元,那么销售每个篮球所获得的利润是_______元,这种篮球每月的销售量是 个(用x的代数式表示) (2)8000元是否为每月销售篮球的最大利润?如果是,说明理由,如果不是,请求出最大月利润,此时篮球的售价应定为多少元?
8000元不是每月最大利润,最大月利润为9000元,此时篮球的售价为70元.
某景区商店销售一种纪念品,每件的进货价为40元.经市场调研,当该纪念品每件的销售价为50元时,每天可销售200件;当每件的销售价每增加1元,每天的销售数量将减少10件.(1)当每件的销售价为52元时,该纪念品每天的销售数量为______件;(2)当每件的销售价x为多少时,销售该纪念品每天获得的利润y最大?并求出最大利润.
解:(1)由题意得:200﹣10×(52﹣50)=200﹣20=180(件), (2)由题意得: y=(x﹣40)[200﹣10(x﹣50)] =﹣10x2+1100x﹣28000 =﹣10(x﹣55)2+2250∴每件销售价为55元时,获得最大利润;最大利润为2250元.
1. 某种商品每件的进价为20元,调查表明:在某段时间内若以每件x元(20 ≤x ≤30)出售,可卖出(300-20x)件,使利润最大,则每件售价应定为 元.
2. 进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系式为 .每月利润w(元)与衬衣售价x(元)之间的函数关系式为 .(以上关系式只列式不化简).
y=2000-5(x-100)
w=[2000-5(x-100)](x-80)
一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
w=[12+2(x-1)][80-4(x-1)] =(10+2x)(84-4x) =-8x2+128x+840 =-8(x-8)2+1352.
解:设生产x档次的产品时,每天所获得的利润为w元, 则
当x=8时,w有最大值,且w最大=1352.
答:该工艺师生产第8档次产品,可使利润最大,最大利润为1352元.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax²+bx-75.其图象如图. (1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?
解:由图可以看出:二次函数y=ax+bx-75过点(5,0),(7,16)将两点坐标代入解析式即可求得:(1)y=-x2+20x-75,即y=-(x-10)2+25
∵-1<0,对称轴x=10,
∴当x=10时,y值最大,最大值为25.即销售单价定为10元时,销售利润最大,为25元;
(2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
(2)显然,当y=16时,x=7和13. 因为函数y=-x+20x-75图象的对称轴为x=10, 因此,点(7,16)关于对称轴的对称点为(13,16) 故销售单价在7 ≤x ≤13时,利润不低于16元.
总利润=单件利润×销售量或总利润=总售价-总成本.
涨价:要保证销售量≥0;降件:要保证单件利润≥0.
利用配方法或公式求最大值或利用函数简图和性质求出.
建立二次函数模型解决实际问题
如图是一个二次函数的图象,现在请你根据给出的坐标系的位置,说出这个二次函数的解析式类型.
(3)y=a(x-h)2+k
(4)y=ax2+bx+c
3.能运用二次函数的图象与性质进行决策.
1.掌握二次函数模型的建立,会把实际问题转化为二次函数问题.
2.利用二次函数解决拱桥及运动中的有关问题.
如图,一座拱桥的纵截面是抛物线的一部分,拱桥的跨度是4.9米,水面宽是4米时,拱顶离水面2米.现在想了解水面宽度变化时,拱顶离水面的高度怎样变化.你能想出办法来吗?
建立平面直角坐标系解答抛物线形问题
怎样建立直角坐标系比较简单呢?
以拱顶为原点,抛物线的对称轴为y轴,建立直角坐标系,如图.
从图看出,什么形式的二次函数,它的图象是这条抛物线呢?
已知水面宽4米时,拱顶离水面高2米,因此点A(2,-2)在抛物线上,由此得出
由于拱桥的跨度为4.9米,因此自变量x的取值范围是:
水面宽3m时 从而因此拱顶离水面高1.125m
现在你能求出水面宽3米时,拱顶离水面高多少米吗?
建立二次函数模型解决实际问题的基本步骤是什么?
利用二次函数的图象和性质求解
建立坐标系解答生活中的抛物线形问题
解法一: 如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
∴可设这条抛物线所表示的二次函数的解析式为y=ax2
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为y=-0.5x2 .
∴-2=a×22∴a=-0.5
当水面下降1m时,水面的纵坐标为y=-3,这时有:
解法二: 如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
因此可设这条抛物线所表示的二次函数的解析式为:y=ax²+2.
此时,抛物线的顶点为(0,2)
即:抛物线过点(2,0)
因此这条抛物线所表示的二次函数为:y=-0.5x²+2
当水面下降1m时,水面的纵坐标为y=-1,这时有:
0=a×22+2,a=-0.5
解法三:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
因此可设这条抛物线所表示的二次函数的解析式为y=a(x-2)²+2
∵抛物线过点(0,0)∴0=a×(-2)²+2∴a=-0.5
因此这条抛物线所表示的二次函数为y=-0.5(x-2) ²+2.
此时,抛物线的顶点为(2,2)
回顾 “最大利润”和 “桥梁建筑”解决问题的过程,你能总结一下解决此类问题的基本思路吗?与同伴交流.
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
5.检验结果的合理性.
【思考】“二次函数应用”的思路
有一座抛物线形拱桥,正常水位时桥下水面宽度为 20m,拱顶距离水面 4 m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式.
解:设该拱桥形成的抛物线的解析式为y=ax2.∵该抛物线过(10,-4),∴-4=100a,a=-0.04∴y=-0.04x2 .
利用二次函数解决运动中抛物线形问题
例2 如图,一名运动员在距离篮球圈中心4m(水平距离)远处跳起投篮,篮球准确落入篮圈,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m,如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:如图,建立直角坐标系.则点A的坐标是(1.5,3.05),篮球在最大高度时的位置为B(0,3.5).以点C表示运动员投篮球的出手处.
设以y轴为对称轴的抛物线的解析式为 y=a(x-0)2+k ,即y=ax2+k.而点A,B在这条抛物线上,所以有
某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.(1)求水柱所在抛物线(第一象限部分)的函数表达式;(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.
解:(1)设水柱所在抛物线(第一象限部分)的函数表达式为y=a(x﹣3)2+5(a≠0),将(8,0)代入y=a(x﹣3)2+5,得:25a+5=0,解得:a=﹣0.2,∴水柱所在抛物线(第一象限部分)的函数表达式为y=﹣0.2(x﹣3)2+5(0<x<8).(2)当y=1.8时,有﹣0.2(x﹣3)2+5=1.8,解得:x1=﹣1,x2=7,因此为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心7米以内.(3)当x=0时,y=﹣0.2(x﹣3)2+5=3.2.设改造后水柱所在抛物线(第一象限部分)的函数表达式为y=﹣0.2x2+bx+3.2,∵该函数图象过点(16,0),∴0=﹣0.2×162+16b+3.2,解得:b=3,∴改造后水柱所在抛物线(第一象限部分)的函数表达式为 y=﹣0.2x2+3x+3.2=﹣0.2(x﹣7.5)2+14.45.∴扩建改造后喷水池水柱的最大高度为14.45米.
1. 足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在 s后落地.
2. 如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数解析式为 ,那么铅球运动过程中最高点离地面的距离为 米.
3. 某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )A.50m B.100m C.160m D.200m
某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m,抛物线拱高为5.6m.(1)在如图所示的平面直角坐标系中,求抛物线的表达式.
解:(1)设抛物线的表达式为y=ax2 . ∵点B(6,﹣5.6)在抛物线的图象上, ∴﹣5.6=36a, ∴抛物线的表达式为
(2)现需在抛物线AOB的区域内安装几扇窗户,窗户的底边在AB上,每扇窗户宽1.5m,高1.6m,相邻窗户之间的间距均为0.8m,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m.请计算最多可安装几扇这样的窗户?
(2)设窗户上边所在直线交抛物线于C,D两点,D点坐标为(k,t),已知窗户高1.6m,∴t=﹣5.6﹣(﹣1.6)=﹣4∴ ,解得k= ,即k1≈5.07,k2≈﹣5.07 ∴CD=5.07×2≈10.14(m)设最多可安装n扇窗户,∴1.5n+0.8(n﹣1)+0.8×2≤10.14,解得n≤4.06.则最大的正整数为4.答:最多可安装4扇窗户.
悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接.已知两端主塔之间的水平距离为900 m,两主塔塔顶距桥面的高度为81.5 m,主悬钢索最低点离桥面的高度为0.5 m. (1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
解:根据题意,得抛物线的顶点坐标为(0,0.5),对称轴为y轴,设抛物线的函数表达式为y=ax2+0.5.抛物线经过点(450,81.5),代入上式,得 81.5=a•4502+0.5.解得故所求表达式为
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
当x=450﹣50=400(m)时,得
(二次函数的图象和性质)
(实物中的抛物线形问题)
能够将实际距离准确的转化为点的坐标;选择运算简便的方法.
数学九年级上册第二十二章 二次函数22.3 实际问题与二次函数优质课ppt课件: 这是一份数学九年级上册第二十二章 二次函数22.3 实际问题与二次函数优质课ppt课件,共36页。PPT课件主要包含了新课导入,1yax2,2yax2+k,-2-2●,●2-2,合作探究,设二次函数解析式为,例题解析,当x8时则,所以此球不能投中等内容,欢迎下载使用。
数学22.3 实际问题与二次函数说课ppt课件: 这是一份数学22.3 实际问题与二次函数说课ppt课件,共10页。PPT课件主要包含了课件说明,整理后得等内容,欢迎下载使用。
人教版九年级上册第二十二章 二次函数22.3 实际问题与二次函数背景图课件ppt: 这是一份人教版九年级上册第二十二章 二次函数22.3 实际问题与二次函数背景图课件ppt,文件包含第2课时实际问题与二次函数2教案doc、第2课时实际问题与二次函数2导学案doc、第2课时最大利润问题pptx等3份课件配套教学资源,其中PPT共0页, 欢迎下载使用。













