




- 24.2.1《点和圆的位置关系》PPT课件 课件 9 次下载
- 24.2.2《直线和圆的位置关系》PPT课件 课件 11 次下载
- 24.4《 弧长和扇形面积》PPT课件 课件 15 次下载
- 25.1.1《随机事件》PPT课件 课件 9 次下载
- 25.1.2《概率》PPT课件 课件 9 次下载
初中数学人教版九年级上册24.3 正多边形和圆公开课课件ppt
展开正多边形的相关概念及计算
观察上边的美丽图案,思考下面的问题:(1)这些都是生活中经常见到的利用正多边形得到的物体,你能找出正多边形吗?
(2)你知道正多边形和圆有什么关系吗?怎样做一个正多边形呢?
3. 会应用正多边形和圆的有关知识解决实际问题.
1. 了解正多边形和圆的有关概念.
2. 理解并掌握正多边形半径、中心角、边心距、边长之间的关系.
问题1 什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
问题2 矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
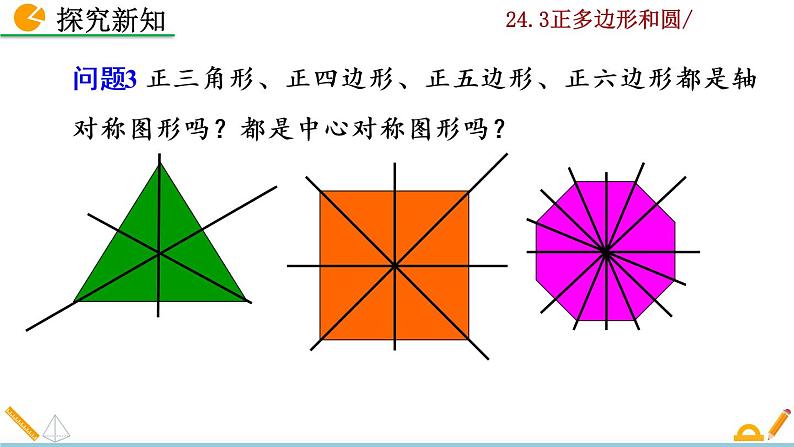
问题3 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
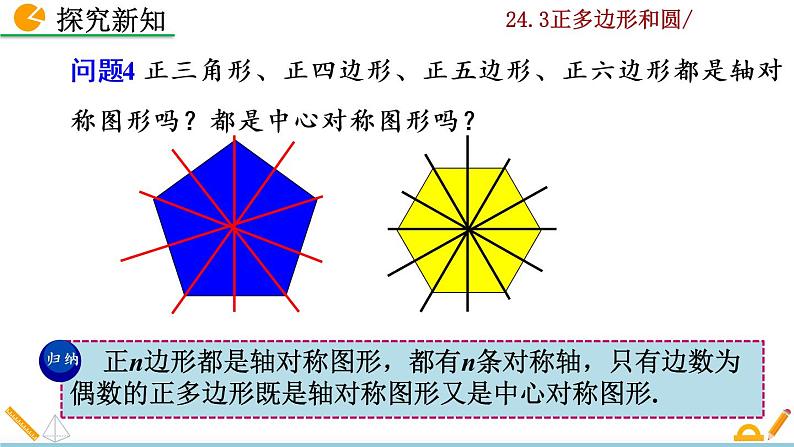
正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形既是轴对称图形又是中心对称图形.
问题4 正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
问题1 以正四边形为例,根据对称轴的性质,你能得出什么结论?
EF是边AB、CD的垂直平分线,∴OA=OB,OD=OC.GH是边AD、BC的垂直平分线,∴OA=OD;OB=OC.∴OA=OB=OC=OD.
∴正方形ABCD有一个以点O为圆心的外接圆.
AC是∠DAB及∠DCB的角平分线,BD是∠ABC及∠ADC的角平分线,
∴OE=OH=OF=OG.
∴正方形ABCD还有一个以点O为圆心的内切圆.
1.所有的正多边形是不是也都有一个外接圆和一个内切圆?
任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.
2.一个正多边形的各个顶点在同一个圆上?
3.所有的多边形是不是都有一个外接圆和内切圆?
一个正多边形的各个顶点在同一个圆上,则这个正多边形就是这个圆的一个内接正多边形,圆叫做这个正多边形的外接圆.
多边形不一定有外接圆和内切圆,只有是正多边形时才有,任意三角形都有外接圆和内切圆.
正多边形的外接圆和内切圆的公共圆心,叫作正多边形的中心.
外接圆的半径叫作正多边形的半径.
内切圆的半径叫作正多边形的边心距.
正多边形的外角=中心角
如图,已知半径为4的圆内接正六边形ABCDEF: ①它的中心角等于 度 ; ② OC BC (填>、<或=); ③△OBC是 三角形; ④圆内接正六边形的面积是 △OBC面积的 倍. ⑤圆内接正n边形面积公式:_______________________.
例1 有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (精确到0.1 m2).
利用勾股定理,可得边心距
解:过点O作OM⊥BC于M.
1.如图所示,正五边形ABCDE内接于⊙O,则∠ADE的度数是 ( )A.60° B.45° C. 36° D. 30°
2.作边心距,构造直角三角形.
1.连半径,得中心角;
方法归纳 :圆内接正多边形的辅助线
2. 已知直角三角形两条直角边的和等于8,两条直角边各为多少时,这个直角三角形的面积最大,最大值是多少?
广东省怀集县中洲镇泰来学校 李周林
解:∵直角三角形两直角边之和为8,设一边长x∴ 另一边长为8-x。 则该直角三角形面积:S=(8-x)x÷2 即当x= =4,另一边为4时,S有最大值 =8∴当两直角边都是4时,直角面积最大,最大值为8.
1.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5= 度
解析:由多边形的外角和等于360°可知,∠1+∠2+∠3+∠4+∠5=360°.
2. 若正多边形的边心距与半径的比为1:2,则这个多边形的边数是 .
4. 要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径
3.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为 度.(不取近似值)
1. 如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
解:∵正方形的面积等于4,
∴正方形的边长AB=2.
则圆的直径AC=2 ,∴⊙O的半径=
∴点P到各边距离之和=3BD=3×6=18.
解:过P作AB的垂线,分别交AB、DE于H、K,连接BD,作CG⊥BD于G.
∴P到AF与CD的距离之和,及P到EF、BC的距离之和均为HK的长.
∵六边形ABCDEF是正六边形,∴AB∥DE,AF∥CD,BC∥EF,
∵BC=CD,∠BCD=∠ABC=∠CDE=120°,
∴∠CBD=∠BDC=30°,BD∥HK,且BD=HK.∴CG= BC=
∴BD=2BG=2× =2× 3 =6.
如图,M,N分别是☉O内接正多边形AB,BC上的点,且BM=CN.(1)求图①中∠MON=_______;图②中∠MON= ; 图③中∠MON= ;(2)试探究∠MON的度数与正n边形的边数n的关系.
添加辅助线的方法:连半径,作边心距
任何正多边形都有一个外接圆和一个内切圆.所有正多边形都是轴对称图形,边数为偶数时,它既是轴对称图形又是中心对称图形
正多边形和圆有什么关系? 你能借助圆画一个正多边形吗?
2. 掌握画正多边形的关键——等分圆周的两种方法:一是量角器等分圆周;二是用尺规作图等分圆周.
1. 掌握正多边形的画法.
多姿多彩的正多边形:观察生活中的正多边形图案.
由于正多边形在生产、生活实际中有广泛的应用性,所以会画正多边形应是学生必备能力之一. 怎样画一个正多边形呢? 问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.
①用量角器度量,使∠AOB=∠BOC=∠COA=120°. ②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
你能用以上方法画出正四边形、正五边形、正六边形吗?
你能尺规作出正四边形、正八边形吗?
只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形……
你能尺规作出正六边形、正三角形、正十二边形吗?
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形. 先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
说说作正多边形的方法有哪些?
(1)用量角器等分圆周作正n边形; (2)用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正三角形.
例 已知☉O和☉O上的一点A(如图).求作☉O的内接正方形ABCD和内接正六边形AEFCGH;
解:作法:①作直径AC;②作直径BD⊥AC;③依次连接A、B、C、D四点.∴四边形ABCD即为☉O的内接正方形.④分别以A、C为圆心,OA的长为半径作弧,交☉O于E、H、F、G;⑤顺次连接A、E、F、C、G、H各点;∴六边形AEFCGH为☉O的内接正六边形,如图所示.
画一个半径为2cm的正五边形,再作出这个正五边形的各条对角线,画出一个五角星.
广东省怀集县大岗镇中心初级中学 石迎伦
在图中,用尺规作图画出圆O的内接正三角形.
作法:1.作出圆的任意一条半径,2.作半径的垂直平分线,交圆于点A、B,3.分别以A、B为圆心,线段AB的长为半径作弧,两户交于点C,连接AC、BC.则△ABC即为所求.
利用量角器画一个边长为2cm的正六边形.作法:如图,以2cm为半径作一个⊙O,用量角器画一个等于 的圆心角,它对着一段弧,然后在圆上依次截取与这条弧相等的弧,就得到圆的6个等分点,顺次连接各分点,即可得出正六边形.
一个平面封闭图形内(含边界)任意两点距离的最大值称为该图形的“直径”,封闭图形的周长与直径之比称为图形的“周率”,下面四个平面图形(依次为正三角形、正方形、正六边形、圆)的周率从左到右依次记为a1,a2,a3,a4,则下列关系中正确的是( )A.a4>a2>a1 B.a4>a3>a2C.a1>a2>a3D.a2>a3>a4
作法:如图,分别以⊙O的四等分点A,B,E,F为圆心,以⊙O的半径长为半径,画8条弧与⊙O相交,就可以把⊙O分成12等份,依次连接各等分点,即得到正十二边形.
1.画正多边形的方法:
由于同圆中相等的圆心角所对的弧相等,因此作相等的圆心角就可以等分圆周,从而得到相应的正多边形.
1.用量角器等分圆2.尺规作图等分圆
数学九年级上册24.3 正多边形和圆图文ppt课件: 这是一份数学九年级上册24.3 正多边形和圆图文ppt课件,共29页。PPT课件主要包含了教学目标,教学重难点,情境引入,合作学习,雪花晶体,储物柜,正多边形,各边相等,各角相等,缺一不可等内容,欢迎下载使用。
初中数学人教版九年级上册24.3 正多边形和圆集体备课课件ppt: 这是一份初中数学人教版九年级上册24.3 正多边形和圆集体备课课件ppt,文件包含2正多边形和圆pptx、1正多边形和圆pptx等2份课件配套教学资源,其中PPT共64页, 欢迎下载使用。
初中数学人教版九年级上册第二十四章 圆24.3 正多边形和圆背景图ppt课件: 这是一份初中数学人教版九年级上册第二十四章 圆24.3 正多边形和圆背景图ppt课件,共17页。PPT课件主要包含了正多边形的定义,中心角,半径R,边心距r,思考题,每个外角,正多边形边数,边心距,怎样画正多边形,连接OB则OBR等内容,欢迎下载使用。













