15.2021年高考数学（理）总复习（高考研究课件 高考达标检测 教师用书）第七单元 平面向量 （6份打包）

高考达标检测（二十二） 平面向量的数量积及应用

一、选择题

1．(2017·江西八校联考)已知两个非零向量a，b满足a·(a－b)＝0，且2|a|＝|b|，则〈a，b〉＝(　　)

A．30°　　　　　　　　　 　B．60°

C．120°   D．150°

解析：选B　由题知a2＝a·b，而cos〈a，b〉＝＝＝，所以〈a，b〉＝60°，故选B.

2．(2016·长春三模)若|a＋b|＝|a－b|＝2|a|，则向量a－b与b的夹角为(　　)

A.   B.

C.   D.

解析：选D　由|a＋b|＝|a－b|⇒|a＋b|2＝|a－b|2⇒a·b＝0，|a－b|＝2|a|⇒|a－b|2＝4|a|2⇒|b|＝|a|，设a－b与b的夹角为θ，则cos θ＝＝＝＝－，又θ∈[0，π]，所以θ＝，故选D.

3．O是△ABC所在平面内的一点，且满足(－)·(＋－2)＝0，则△ABC的形状一定是(　　)

A．正三角形   B．直角三角形

C．等腰三角形   D．斜三角形

解析：选C　∵(－)·(＋－2)＝(－)·[(－)＋(－)]＝(－)·(＋)＝·(＋)＝(－)·(＋)＝||2－||2＝0，所以||＝||，∴△ABC为等腰三角形．

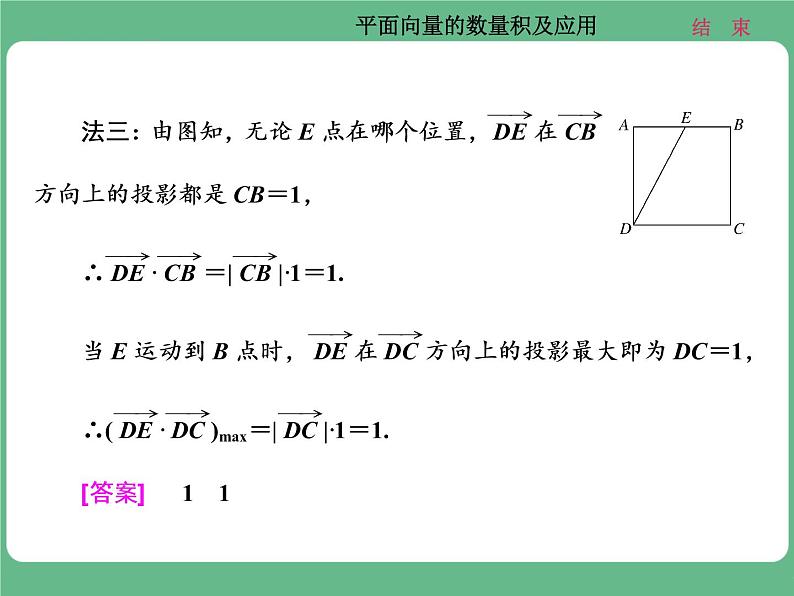
4.如图，在矩形ABCD中，AB＝，BC＝2，点E为BC的中点，点F在边CD上，若·＝，则·的值是(　　)

A.   B．2

C．0   D．1

解析：选A　∵＝＋，·＝·(＋)＝·＋·＝·＝||＝，∴||＝1，||＝－1，∴·＝(＋)·(＋)＝·＋·＝－(－1)＋1×2＝－2＋＋2＝，故选A.

5．(2017·东北三校联考)在△ABC中，A＝120°，·＝－1，则||的最小值是(　　)

A.   B．2

C.   D．6

解析：选C　在△ABC中，设AB＝c，AC＝b，BC＝a.

因为·＝－1，所以bccos 120°＝－1，即bc＝2，在△ABC中，由余弦定理得：a2＝b2＋c2－2bccos 120°＝b2＋c2＋bc≥3bc＝6，所以a≥，即||的最小值是.

6.已知函数f(x)＝Asin(πx＋φ)的部分图象如图所示，点B，C是该图象与x轴的交点，过点C的直线与该图象交于D，E两点，则(＋)·(－)的值为(　　)

A．－1   B．－

C.   D．2

解析：选D　注意到函数f(x)的图象关于点C对称，因此C是线段DE的中点，＋＝2.

又－＝＋＝，

且||＝T＝×＝1，因此(＋)·(－)＝22＝2，选D.

7．已知菱形ABCD的边长为6，∠ABD＝30°，点E，F分别在边BC，DC上，BC＝2BE，CD＝λCF.若·＝－9，则λ的值为(　　)

A．2   B．3

C．4   D．5

解析：选B　依题意得＝＋＝－，＝＋，因此·＝·＝2－2＋·，于是有×62＋×62×cos 60°＝－9，由此解得λ＝3，选B.

8．(2016·银川调研)已知⊥，||＝，||＝t，若点P是△ABC所在平面内的一点，且＝＋，则·的最大值等于(　　)

A．13   B．15

C．19   D．21

解析：选A　建立如图所示坐标系，则B，C(0，t)，＝，＝(0，t)，＝＋＝t＋(0，t)＝(1,4)，

∴P(1,4)，·＝·(－1，t－4)＝17－≤17－2＝13，当且仅当t＝时，取“＝”．故选A.

二、填空题

9．(2017·兰州诊断)已知向量a，b满足|b|＝4，a在b方向上的投影是，则a·b＝________.

解析：a在b方向上的投影是，设θ为a与b的夹角，则|a|·cos θ＝，a·b＝|a|·|b|·cos θ＝2.

答案：2

10．已知向量α，β是平面内两个互相垂直的单位向量，若(5α－2γ)·(12β－2γ)＝0，  则 | γ | 的最大值是________．

解析：因为α·β＝0，|α|＝|β|＝1，

所以(5α－2γ)·(12β－2γ)＝60α·β－10α·γ－24β·γ＋4γ·γ＝0，

即2|γ|2＝5α·γ＋12β·γ＝(5α＋12β)·γ，当γ与5α＋12β共线时，|γ|最大，

所以4|γ|2＝(5α＋12β)2＝25|α|2＋120α·β＋144|β|2＝25＋144＝169，

所以|γ|＝.

答案：

11．在直角梯形ABCD中，AD∥BC，∠ABC＝90°，AB＝BC＝2，AD＝1，梯形所在平面内一点P满足＋＝2，则·＝________.

解析：以BC，BA为邻边作矩形ABCE，则＋＝，∵＋＝2，故P是BE的中点，连接PC，∴PD＝AB＝1，CP＝AC＝，CD＝＝，   cos∠CPD＝＝－，·＝||·||cos∠CPD＝1××＝－1.

答案：－1

12.如图，已知△ABC中，AB＝AC＝4，∠BAC＝90°，D是BC的中点，若向量＝＋m·，且的终点M在△ACD的内部(不含边界)，则·的取值范围是________．

解析：以A为坐标原点，AB所在直线为x轴建立直角坐标系，则B(4,0)，C(0,4)，D(2,2)，M(1,4m)，m∈，·＝(1,4m)·(－3,4m)＝16m2－3∈(－2,6)．

答案：(－2,6)

三、解答题

13．(2016·西安考前检测)已知向量a＝(2，－1)，b＝(1，x)．

(1)若a⊥(a＋b)，求|b|的值；

(2)若a＋2b＝(4，－7)，求向量a与b夹角的大小．

解：(1)由题意得a＋b＝(3，－1＋x)．

由a⊥(a＋b)，可得6＋1－x＝0，

解得x＝7，即b＝(1,7)，

所以|b|＝＝5.

(2)a＋2b＝(4,2x－1)＝(4，－7)，

故x＝－3，

所以b＝(1，－3)，

所以cos〈a，b〉＝＝＝，

因为〈a，b〉∈[0，π]，

所以a与b夹角是.

14．已知向量m＝，n＝.

(1)若m·n＝1，求cos的值；

(2)记f(x)＝m·n，在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cos B＝bcos C，求函数f(A)的取值范围．

解：m·n＝sincos＋cos2

＝sin＋cos＋

＝sin＋.

(1)∵m·n＝1，

∴sin＝，

cos＝1－2sin2＝，

cos＝－cos＝－.

(2)∵(2a－c)cos B＝bcos C，由正弦定理得

(2sin A－sin C)cos B＝sin Bcos C，

∴2sin Acos B＝sin Ccos B＋sin Bcos C，

∴2sin Acos B＝sin(B＋C)．

∵A＋B＋C＝π，

∴sin(B＋C)＝sin A，且sin A≠0，

∴cos B＝，B＝.∴0<A<.

∴<＋<，<sin<1.

又∵f(x)＝m·n＝sin＋，

∴f(A)＝sin＋，

故1<f(A)<.

故函数f(A)的取值范围是.