初中数学6.2 二元一次方程组的解法教课ppt课件

这是一份初中数学6.2 二元一次方程组的解法教课ppt课件，文件包含62第1课时代入消元法解较简单方程组pptx、第2课时代入消元法解较复杂方程组pptx、第3课时加减消元法解方程组pptx、62二元一次方程组的解法doc、视频鸡兔同笼mp4等5份课件配套教学资源，其中PPT共106页， 欢迎下载使用。
1.理解代入消元法的概念，初步体会解二元一次方程组的基本思想——“消元”.（重点）2.会用代入消元法解未知数系数含1或-1的方程组.(难点）
思考：视频中的问题你知道怎么解吗？
《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题”雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
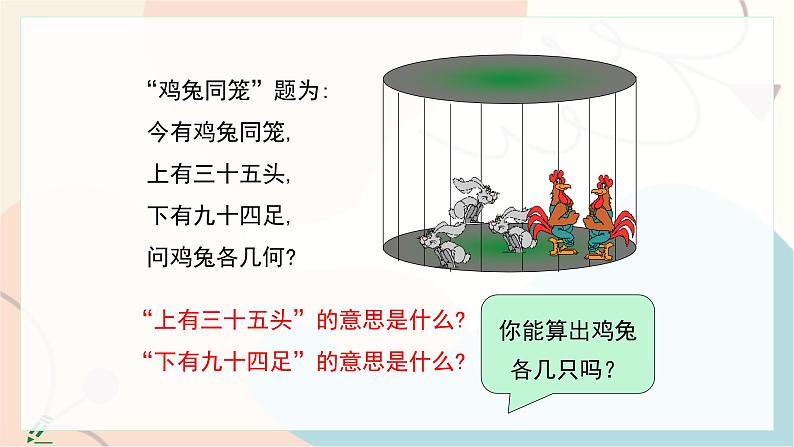
“鸡兔同笼”题为: 今有鸡兔同笼, 上有三十五头, 下有九十四足, 问鸡兔各几何?
“上有三十五头”的意思是什么?“下有九十四足”的意思是什么?
你能算出鸡兔各几只吗？
问题1 你能用一元一次方程解决鸡兔同笼的问题吗？
解：设鸡有x只，则兔有_________只.根据题意列方程，得
2x+4(35-x)=94. *
解这个一元一次方程，得 x=23.
从而，得 35-x=12.
即鸡有23只，兔子有12只.
问题2：如何利用二元一次方程组解决鸡兔同笼问题？
解：设鸡有x只，兔子有y只.依题意，可列方程组
由①，得 y=35-x. ③
将 ③代入②中，得 2x+4(35-x)=94. ④
2x+4(35-x)=94
(4)从中你体会到怎样解二元一次方程组吗？
问题3：一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g？
x + y = 200
y = x + 10
x +( x +10) = 200
求方程组解的过程叫做解方程组
将未知数的个数由多化少，逐一解决的思想，叫做消元思想.
解二元一次方程组的基本思路“消元”
用“代入”的方法进行“消元”，这种解方程组的方法称为代入消元法，简称代入法.
代入法是解二元一次方程组常用的方法之一.
解：将 ①代入②中，得 x+2(x-6)=9.
解这个一元一次方程，得 x=7.
将x=7代入①中，得 y=1.
x=10-y. ③
y=10-x. ③
x-2(10-x)=4.
x=4+2y. ③
用代入消元法解二元一次方程组的过程中，尽可能的选择方程中未知数的系数为±1的方程变形.
x － y = 3 , 3 x － 8 y = 14.
把y=－1代入③,得 x=2.
把③代入②,得 3(y+3)－8y=14.
解：由①,得 x = y + 3 .③
例2 解方程组
解这个方程,得 y=－1.
思考：把③代入①可以吗？
解：由①，得 y = 8－x. ③
5x+3(8－x)=34.
把x = 5代入③，得 y = 3.
x+y=8①5x+3y=34②
观察上面的方程和方程组，你能发现二者之间的联系吗？请你尝试求得方程组的解。（先试着独立完成，然后与你的同伴交流做法）
2．代入前后的方程组发生了怎样的变化?（代入的作用）
做一做 若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程，求m 、n 的值.
根据已知条件可列方程组,得
3m – 2n = 1
3m – 2（1 – 2m）= 1
若方程5x 2m+n + 4y 3m-2n = 9是关于x,y的二元一次方程，求m ,n 的值.
解：根据已知条件，由二元一次方程的定义，可列方程组
方程①可变形为 n=1-2m. ③
将③代入②中，得 3m-2(1-2m) =1.
根据二元一次方程的概念，含未知数的项的次数为1，列出二元一次方程组，从而求出未知数的值.
1.下列各方程组中，应怎样代入消元？
由①，得y=7x –11 ③将③代入②
小技巧： 用代入法时，往往对方程组中系数为1或-1的未知数所在的方程进行变形代入.
2.用代入法解方程组 比较合理的变 形是(　　) A．由①得 B．由①得 C．由②得 D．由②得y＝2x－5
3.方程组 的解是(　　)A. B. C. D.
解：(1)将②直接代入①中，得 2y-(y+1)=3, 解得 y=4.将y=4代入②中，得 x=5.所以原方程组的解为
(2)方程①可变形为 y=2x-5.③ 将③代入②中，得 4x+3(2x-5)=15,解得 x=3.将x=3代入③中，得 y=1.所以原方程组的解为
6.某校组织活动，共有100人参加，要把参加活动的人分成两组，已知第一组人数比第二组人数的2倍少8人，问这两组人数各是多少？
解：设第一组有x人，第二组有y人， 根据题意，可列方程组
答：第一组有64人，第二组有36人.