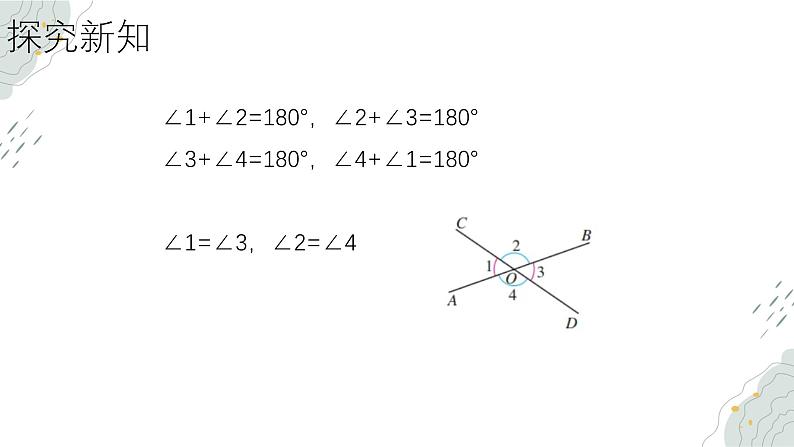
人教版（2024）七年级下册（2024）7.1.1 两条直线相交教课内容ppt课件

这是一份人教版（2024）七年级下册（2024）7.1.1 两条直线相交教课内容ppt课件，共23页。PPT课件主要包含了教学目标，情境导入，探究新知，课堂练习，例题解析，课后练习，课堂总结等内容，欢迎下载使用。
1.理解邻补角、对顶角的概念2.运用邻补角、对顶角的性质解题
观察图片，两条直线是什么位置关系？
如图，取两根木条a，b，将它们钉在一起，并把它们想象成两条直线，就得到一个相交线的模型。在转动木条的过程中，它们所成的角也在变化，你能发现这些角之间不变的关系吗?
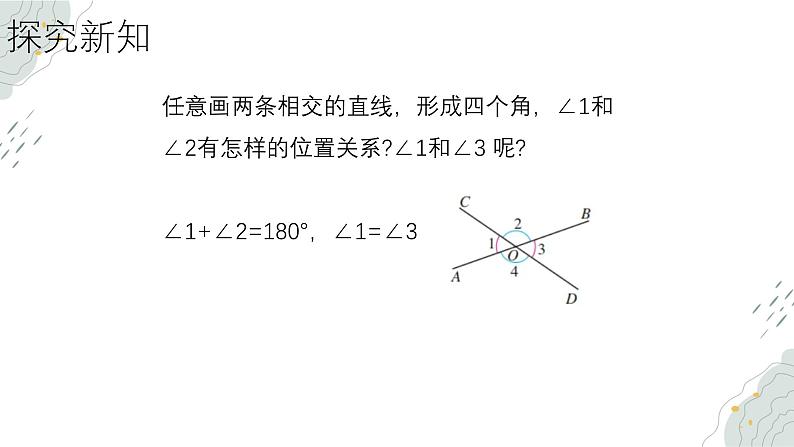
任意画两条相交的直线，形成四个角，∠1和∠2有怎样的位置关系?∠1和∠3 呢?∠1+∠2=180°，∠1=∠3
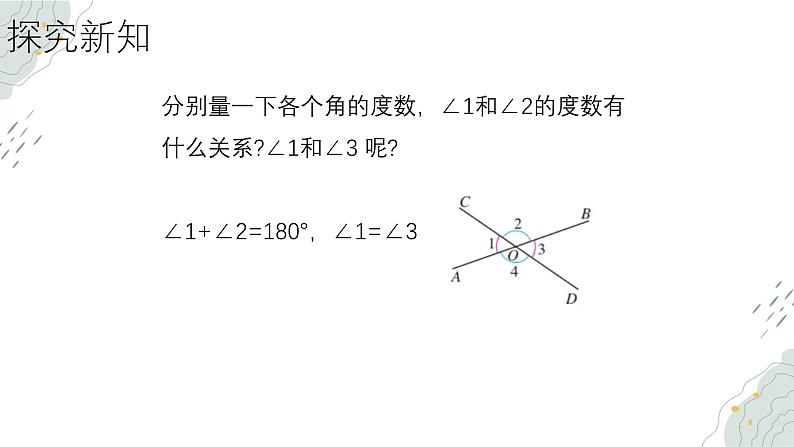
分别量一下各个角的度数，∠1和∠2的度数有什么关系?∠1和∠3 呢?∠1+∠2=180°，∠1=∠3
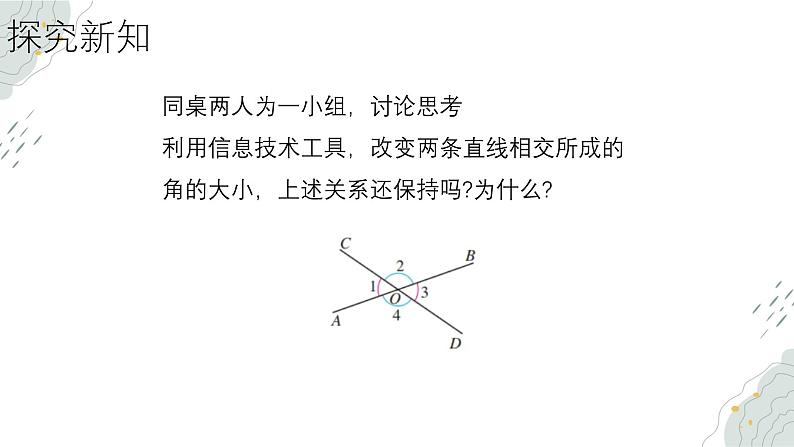
同桌两人为一小组，讨论思考利用信息技术工具，改变两条直线相交所成的角的大小，上述关系还保持吗?为什么?
∠1+∠2=180°，∠2+∠3=180°∠3+∠4=180°，∠4+∠1=180°∠1=∠3，∠2=∠4
∠1和∠2有一条公共边OC，它们的另一边互为反向延长线(∠1和∠2互补)，具有这种位置关系的两个角，互为邻补角
如图，O是直线AB上一点，∠COB=30°，则∠1=__150°__
如图，∠1的邻补角是（ D ）A.∠BOC B.∠BOC和∠AOFC.∠AOF D.∠BOE和∠AOF
∠1和∠3有一个公共顶点O，并且∠1的两边分别是∠3的两边的反向延长线，具有这种位置关系的两个角，互为对顶角
下列各图中，∠1与∠2是对顶角的是（ D ）
下面四个图形中，∠1=∠2一定成立的是（ B ）
下列说法中正确的是（ A ）A.不相等的角一定不是对顶角B.互补的两个角是邻补角C.互补且有一条公共边的两个角是邻补角D.两条直线相交所成的角是对顶角
在图中，∠1=∠3。这个结论还可以通过补角的性质得到：∠1与∠2互补，∠3与∠2互补，由“同角的补角相等”，可得∠1=∠3类似地,可得∠2=∠4这样，可以得到对顶角的性质对顶角相等
“对顶角相等”这个结论的过程，可以写成下面的形式因为 ∠1与∠2互补，∠3与∠2互补所以∠1=∠3(同角的补角相等)
如图，直线a，b 相交，∠1=40°求∠2，∠3，∠4的度数解：由∠1和∠2 互为邻补角，得∠2=180°-∠1=180°-40°=140°由对顶角相等，得∠3=∠1=40°，∠4=∠2=140°
在下列各图中，∠1和∠2是不是对顶角?
(1)有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角(2)有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角(3)邻补角互补，对顶角相等
如图，在相交线的模型中，如果两根木条a，b 所成的角中有一个角∠α=35°，其他三个角分别等于多少度?如果∠α等于 90°，115°，m°呢?
如图，直线AB，CD 相交于点O∠AOC：∠BOC=2：7则∠BOC等于多少度呢?∠AOD呢？