鲁教版（五四学制）（2024）七年级下册4 平行线的判定定理教课内容课件ppt

这是一份鲁教版（五四学制）（2024）七年级下册4 平行线的判定定理教课内容课件ppt，共24页。PPT课件主要包含了∠2与∠4互补，AB∥CD，基本事实公理，利用①证明②③，结论这两直线平行，求证a∥b，找同位角，简述为，符号语言，议一议等内容，欢迎下载使用。
1.能根据“同位角相等，两直线平行”证明“同旁内角互补，两直线平行”，并能利用它们证明“内错角相等，两直线平行”。2.了解证明一个命题的步骤3.掌握并熟练应用平行线的判定方法
1.前面我们探索过哪些两条直线平行的判别条件？
两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行。
2.如图，填空①因为∠1=∠2，根据“ ”所以AB∥CD
两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行。
两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行。
同位角相等，两直线平行
②因为∠2=∠3，根据“ ”所以EF∥GH
③因为______________ 根据“同旁内角互补，两直线平行”所以___________
内错角相等，两直线平行
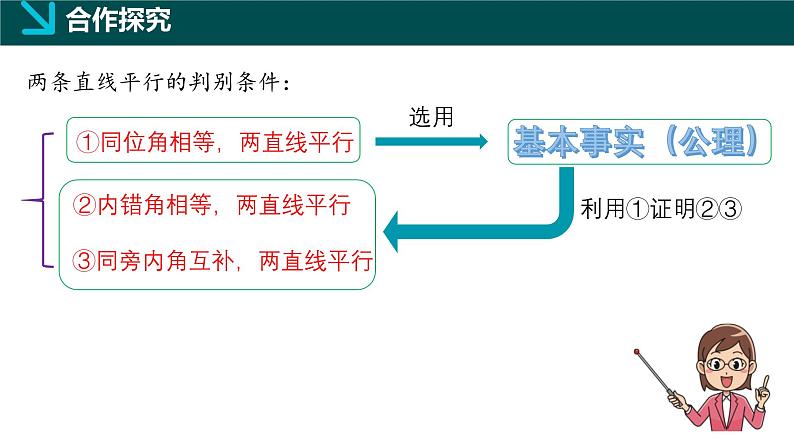
两条直线平行的判别条件：
①同位角相等，两直线平行
②内错角相等，两直线平行
③同旁内角互补，两直线平行
利用“两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行”（简述为“同位角相等，两直线平行”）这个基本事实，证明两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行
学生活动：以小组为单位，讨论以下问题1.命题的条件和结论分别是什么?2.根据题意，如何画出图形。3.根据条件和结论，如何写出已知和求证。4.如何证明？时间大约5分钟
条件：两条直线被第三条直线所截，同旁内角互补
已知：如图，∠1和∠2是直线a，b被直线c截出的同旁内角，且∠1与∠2互补
证明：∵∠3+∠2=180°（平角的定义）∴∠3是∠2的补角（互补的定义）∵∠1是∠2的补角（已知）∴∠1=∠3（同角的补角相等）∴a∥b（同位角相等，两直线平行）
总结：已给的公理，定义和定理以后都可以作为依据，用来证明新的命题。
同旁内角互补，两直线平行。
∵∠1与∠2互补∴a∥b（同旁内角互补，两直线平行）
两条直线被第三条直线所截，如果同旁内角互补，那么这两条两直线平行。
小明利用两块同样的三角板，按下面的方法作出了平行线。你认为他的作法对吗？为什么
两条直线被第三条直线所截，如果内错角相等，那么这两条两直线平行。
已知：如图，∠1和∠2是直线a，b被直线c截出的内错角，且∠1=∠2
学生活动：以小组为单位，讨论如何证明，尽可能想出多种方法，时间5分钟
证明：方法一∵∠1=∠2（已知）∠1=∠3（对顶角相等）∴∠2=∠3（等量代换）∴a∥b（同位角相等，两直线平行）
证明：方法二∵∠1=∠2（已知）∠1+∠3=180°（平角的定义）∴∠2+∠3=180°（等量代换）∴∠2与∠3互补（互补的定义）∴a∥b（同旁内角互补，两直线平行）
内错角相等，两直线平行。
∵∠1=∠2∴a∥b（内错角相等，两直线平行）
证明一个命题的一般步骤
公理：同位角相等，两直线平行
定理：内错角相等，两直线平行
同旁内角互补，两直线平行
两条直线平行的判别条件
1.弄清命题的条件和结论2.根据题意画出图形。3.根据条件和结论，写出已知和求证。4.分析证明思路，写出证明过程
1.如图，下列推理是否正确？为什么？（1）∵∠1=∠2 ∴AB∥CD（2）∵∠4+∠5=180° ∴EF∥GH（3）∵∠2=∠4 ∴EF∥GH（4）∵∠3+∠6=180° ∴AB∥CD
2.已知：如图，直线a，b被直线c所截，且∠1+∠2=180°求证：a∥b你有几种证明方法
证明：方法一∵∠1+∠2=180°（已知）∴∠2是∠1的补角（互补的定义）∵∠1+∠3=180°（平角的定义）∴∠3是∠1的补角（互补的定义）∴∠2=∠3（同角的补角相等）∴a∥b（同位角相等，两直线平行）
可以找同位角，内错角，或同旁内角
证明：方法二∵∠1+∠2=180°（已知）∴∠2是∠1的补角（互补的定义）∵∠1+∠3=180°（平角的定义）∴∠3是∠1的补角（互补的定义）∴∠2=∠3（同角的补角相等）∴a∥b（内错角相等，两直线平行）
证明：方法三∵∠1+∠2=180°（已知）∴∠2是∠1的补角（互补的定义）∵∠1=∠3（对顶角相等）∴∠3+∠2=180°（等量代换）∴∠2与∠3互补（互补的定义）∴a∥b（同旁内角互补，两直线平行）
已知：如图，BP交CD于点P，∠ABP+∠BPC=180°，∠1=∠2求证：EB∥PF
证明：∵∠ABP+∠BPC=180°（已知）∴∠ABP是∠BPC的补角（互补的定义）∵∠BPC+∠BPD=180°（平角的定义）∴∠BPD是∠BPC的补角（互补的定义）∴∠ABP=∠BPD（同角的补角相等）∵∠1=∠2（已知）∴∠ABP-∠1=∠BPD-∠2（等式的性质）即∠EBP=∠FPB∴EB∥PF（内错角相等，两直线平行）
如图，木工师傅经常用一把直角尺画出两条平行的直线a和b，你知道这样做的道理吗？
道理：内错角相等，两直线平行
一、证明一个命题的一般步骤是什么？
1.同位角相等，两直线平行
2.内错角相等，两直线平行
3.同旁内角互补，两直线平行
二、两条直线平行的判别条件
1.如图，下列能判定AB∥CD的条件有（ ）①∠B+∠BCD=180°②∠1=∠2③∠3=∠4④∠B=∠5A、1个 B、2个 C、3个 D、4个
2.已知：如图，CD平分∠ACB，∠DCB=40°，∠AED=80°求证：DE∥BC
证明：∵CD平分∠ACB，∠DCB=40°（已知）∴∠ACB=2∠DCB=80°（角平分线定义）∵∠AED=80°（已知）∴∠ACB=∠AED∴DE∥BC（同位角相等，两直线平行）
必做题：课本47页随堂练习2选做题：本节同步练习