







所属成套资源:华东师大版数学八下PPT课件+教案+学案全册
数学八年级下册17.5实践与探索公开课ppt课件
展开
这是一份数学八年级下册17.5实践与探索公开课ppt课件,文件包含华师大版数学八年级下册175《实践与探索》课件pptx、华师大版数学八年级下册175《实践与探索》教案docx、华师大版数学八年级下册175《实践与探索》学案doc等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
1.能根据一次函数的图象求二元一次方程组的解. 2.能通过数形结合说出一次函数与一元一次方程及一元一次 不等式的联系. 3.会图象上获取信息的能力,利用数形结合解决实际问题.
在前几节课里,我们分别学习了一次函数,一次函数的图象,一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数图象的应用。
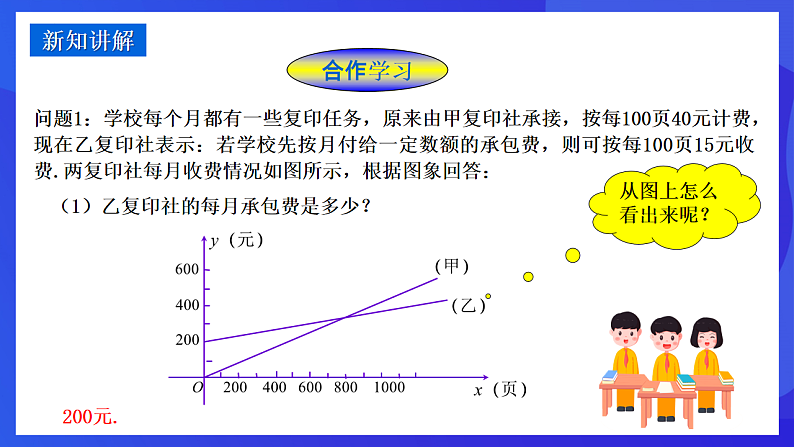
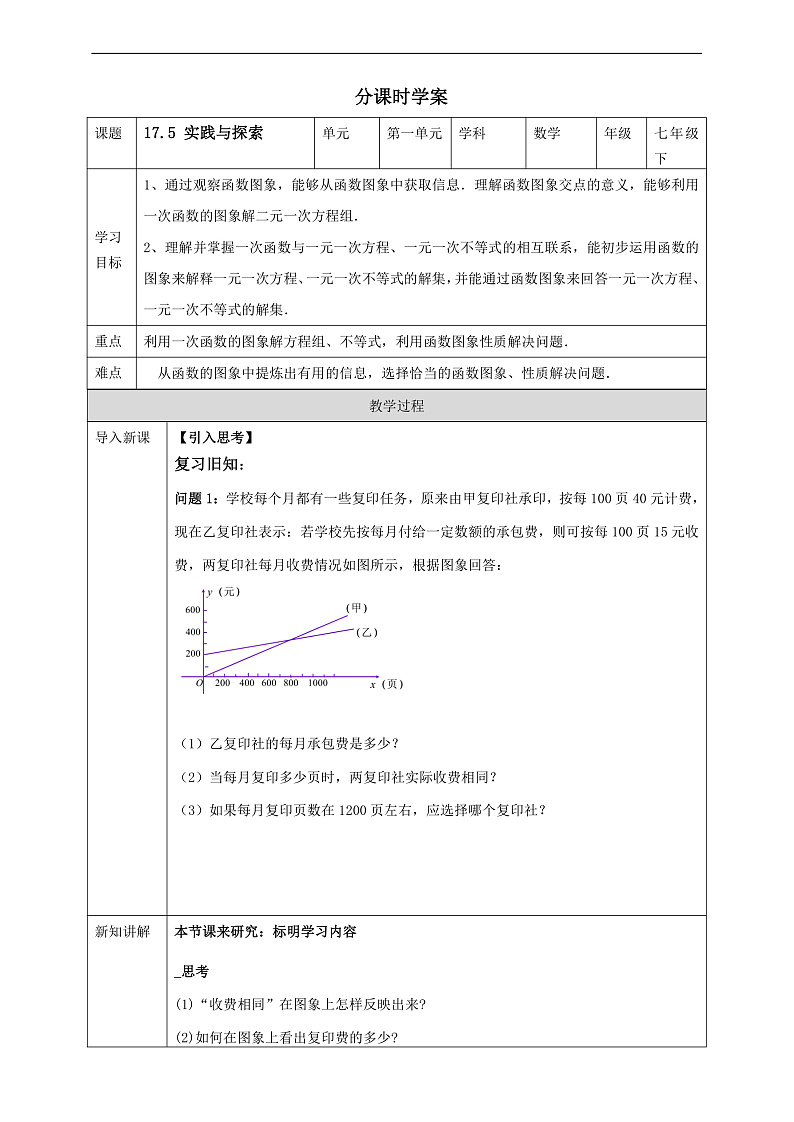
问题1:学校每个月都有一些复印任务,原来由甲复印社承接,按每100页40元计费,现在乙复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印社每月收费情况如图所示,根据图象回答:
(1)乙复印社的每月承包费是多少?
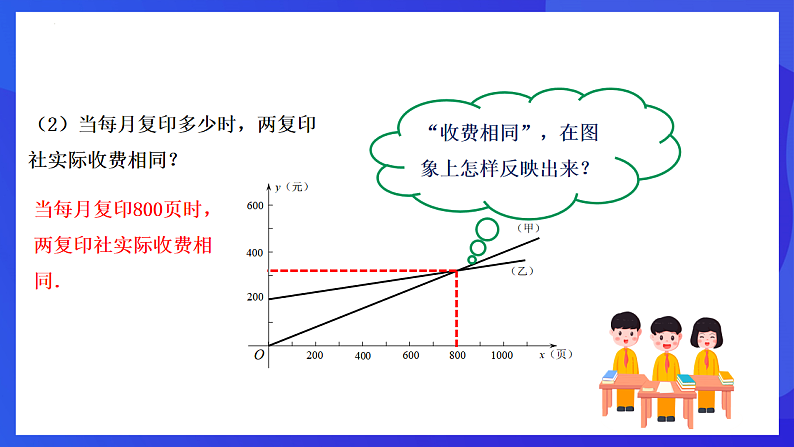
(2)当每月复印多少时,两复印社实际收费相同?
“收费相同”,在图象上怎样反映出来?
当每月复印800页时,两复印社实际收费相同.
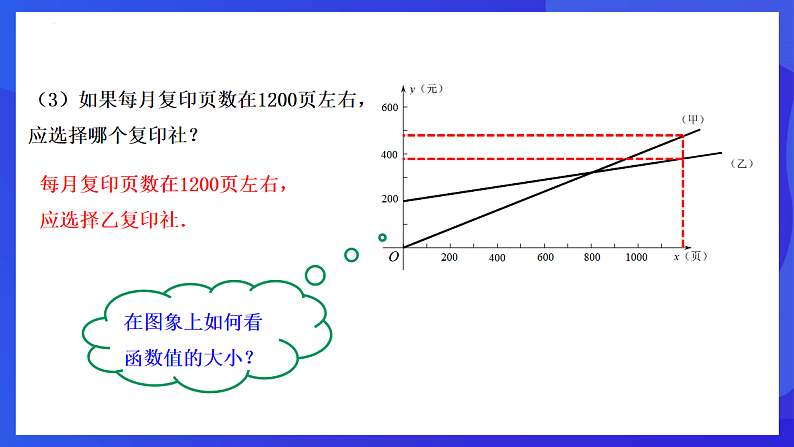
(3)如果每月复印页数在1200页左右,应选择哪个复印社?
每月复印页数在1200页左右,应选择乙复印社.
在图象上如何看函数值的大小?
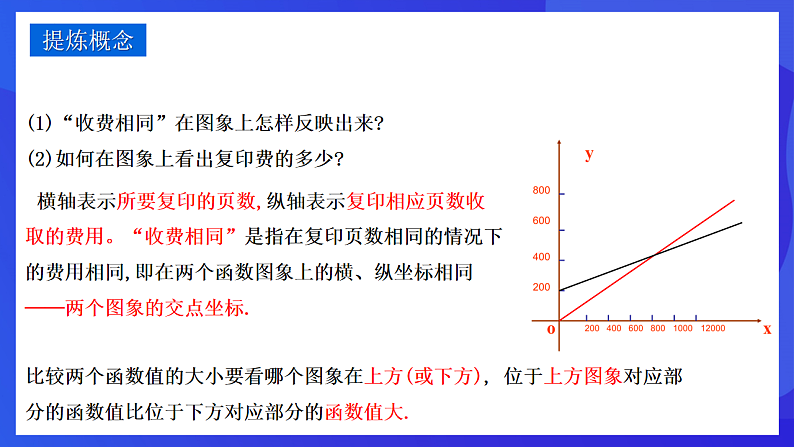
(1)“收费相同”在图象上怎样反映出来?(2)如何在图象上看出复印费的多少?
横轴表示所要复印的页数,纵轴表示复印相应页数收取的费用。“收费相同”是指在复印页数相同的情况下的费用相同,即在两个函数图象上的横、纵坐标相同──两个图象的交点坐标.
比较两个函数值的大小要看哪个图象在上方(或下方), 位于上方图象对应部分的函数值比位于下方对应部分的函数值大.
由函数图象解答问题时,首先要明确横、纵轴表示的含义, 函数图象的交点坐标表示两个图象上横、纵坐标都相同的点,在横轴上的一定取值范围内,位于上方图象的函数值要比位于下方图象的函数值大.
一般地,从函数图象上观察得出值是一个估计值,图象画得越准确, 观察得越仔细,所得的值就越准确.
解: 在直角坐标系中画出两条直线,如图所示.
一次函数与二元一次方程(组)
1.一次函数与二元一次方程的关系:
每对函数值都是方程的一组解
2.一次函数与二元一次方程(组)的关系:
解:有图象可知:(1)当x=-2时,y等于0.(2)当x>-2时,y大于0.
从“数”的角度来看,一次函数y=kx+b(k≠0)的函数值是0时,对应的x的值就是一元一次方程 kx+b=0的解;当一次函数y=kx+b的值大于0时,对应部分x的取值的集合,就是不等式 kx+b>0的解集;当一次函数y=kx+b的值小于0时,对应部分x的取值的集合,就是不等式 kx+b<0的解集.
从“形”的角度看,直线 y=kx+b(k≠0)与x轴交点的横坐标就是方程 kx+b=0的解;直线 y=kx+b位于x轴上方部分对应的x的值的集合就是不等式 kx+b>0的解集;直线 y=kx+b位于x轴下方部分对应的x的值的集合就是不等式 kx+b<0的解集.
问题3:为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:能否据此寻求V和t之间的函数关系式?
分析:在平面直角坐标系中描出这些数值所对应的点.我们发现,这些点大致位于同一条直线上,可知V和t之间近似地符合一次函数关系.
把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
解:设V和t的函数关系式是V =kt +b(k≠0)根据题意,得 ,解得 .所以V与t的函数关系式可能是: V =0.04t+999.9.
我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究. 常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.
1.如图,一次函数y1=k1x+b1与y2=k2x+b2的图象相交于A(3,2),则不等式k2x+b2>k1x+b1的解集为_________.
同理,由2x-y=2,可得y=2x-2
得l1,l2的交点为P(2,2).
3.画出函数y=2x+6的图象,利用图象:(1)求方程2x+6=0的解;(2)求不等式2x+6>0的解;(3)若−2≤y≤2求x的取值范围.
解:图象为:(1)观察图象知:该函数图象经过点 (−3,0),故方程2x+6=0的解为x=−3;(2)观察图象知:当x>−3时,y>0,故不等式2x+6>0的解为x>−3;(3)当−2≤y≤2时,−4≤x≤−2.
求实际问题中的函数关系式的基本方法:一是找_____________建立函数关系式,基本步骤如下: (1)审清题意; (2)找准相等关系; (3)确定自变量和因变量,选用适当的字母表示;
(4)列出相关数量的关系式表示相等关系; (5)写出关系式.二是用______________,基本步骤如下: (1)设出待求的函数关系式; (2)把已知条件代入函数关系式,得到方程或方程组;(3)解方程或方程组,求出待定系数的值;(4)写出函数关系式.
2.如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=−x−2与坐标轴交于B、D两点,两线的交点为P点.(1)求△APB的面积;(2)利用图象求当x取何值时,y1
相关课件
这是一份初中数学17.5实践与探索课文内容ppt课件,共46页。PPT课件主要包含了逐点学练,本节小结,作业提升,学习目标,本节要点,学习流程,知识点,感悟新知,1求b的值,实践与探索等内容,欢迎下载使用。
这是一份初中数学华师大版八年级下册17.5实践与探索课文课件ppt,共21页。PPT课件主要包含了学习目标,乙复印社,知识精讲,要点归纳,典例解析,总结提升,针对练习,解得x265,x-3,-30等内容,欢迎下载使用。
这是一份初中数学华师大版八年级下册17.5实践与探索教学课件ppt,共14页。PPT课件主要包含了利用图象解方程组,情境导入,①列表,②描点,③连线,y2x-5,y-x+1,2-1,的解是,y=-1等内容,欢迎下载使用。










