初中第18章 平行四边形18.1 平行四边形的性质精品ppt课件

这是一份初中第18章 平行四边形18.1 平行四边形的性质精品ppt课件，文件包含华师大版数学八年级下册1812《平行四边形的性质》课件pptx、华师大版数学八年级下册1812《平行四边形的性质》教案docx、华师大版数学八年级下册1812《平行四边形的性质》学案doc等3份课件配套教学资源，其中PPT共20页， 欢迎下载使用。
1．掌握平行四边形对角线互相平分的性质；　 2．经历对平行四边形性质的猜想与证明的过程，渗透转化思想，体 会图形性质探究的一般思路．
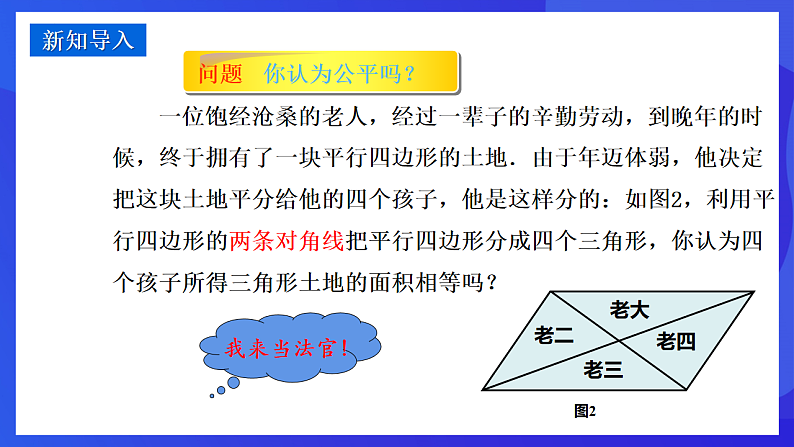
　　一位饱经沧桑的老人，经过一辈子的辛勤劳动，到晚年的时候，终于拥有了一块平行四边形的土地．由于年迈体弱，他决定把这块土地平分给他的四个孩子，他是这样分的：如图2，利用平行四边形的两条对角线把平行四边形分成四个三角形，你认为四个孩子所得三角形土地的面积相等吗？
两组对边分别平行的四边形叫平行四边形
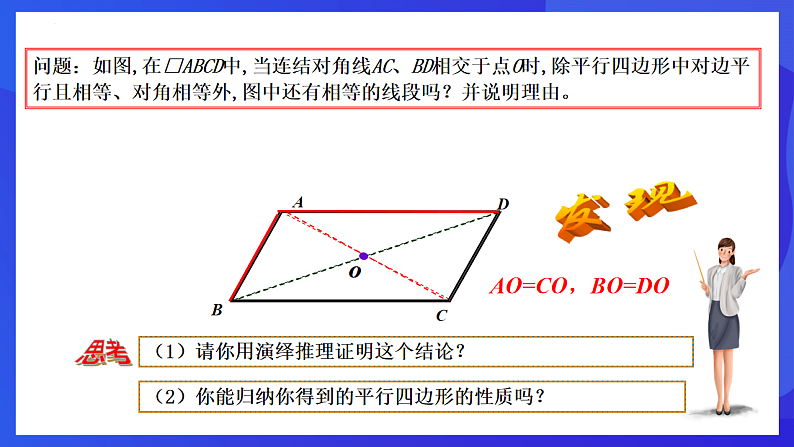
问题：如图,在□ABCD中,当连结对角线AC、BD相交于点O时,除平行四边形中对边平行且相等、对角相等外,图中还有相等的线段吗？并说明理由。
AO=CO，BO=DO
（2）你能归纳你得到的平行四边形的性质吗？
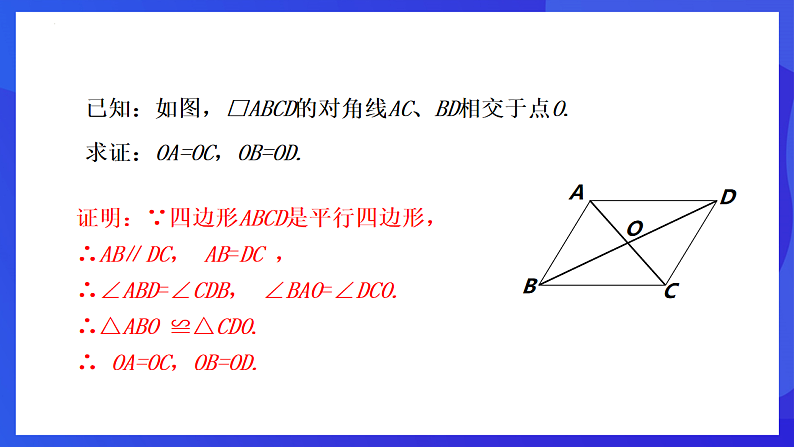
已知：如图，□ABCD的对角线AC、BD相交于点O.
证明：∵四边形ABCD是平行四边形，∴AB∥DC， AB=DC ，∴∠ABD=∠CDB， ∠BAO=∠DCO.∴△ABO ≌△CDO.∴ OA=OC，OB=OD.
求证：OA=OC，OB=OD.
如图□ ABCD 的两条对角线AC、BD相交于点O．
定理3 平行四边形的对角线互相平分．
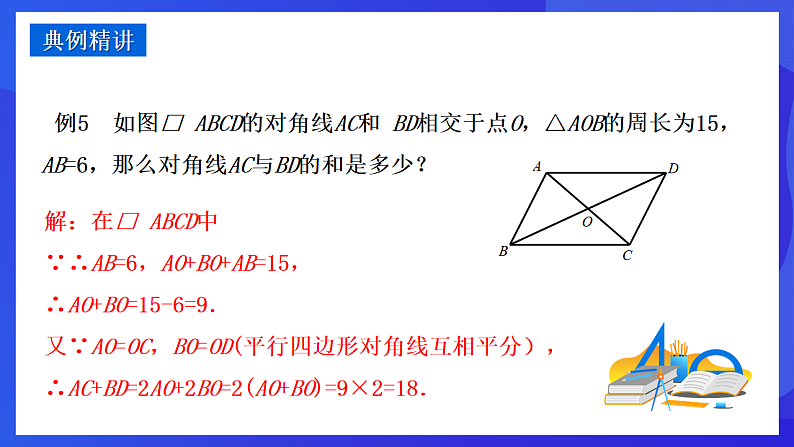
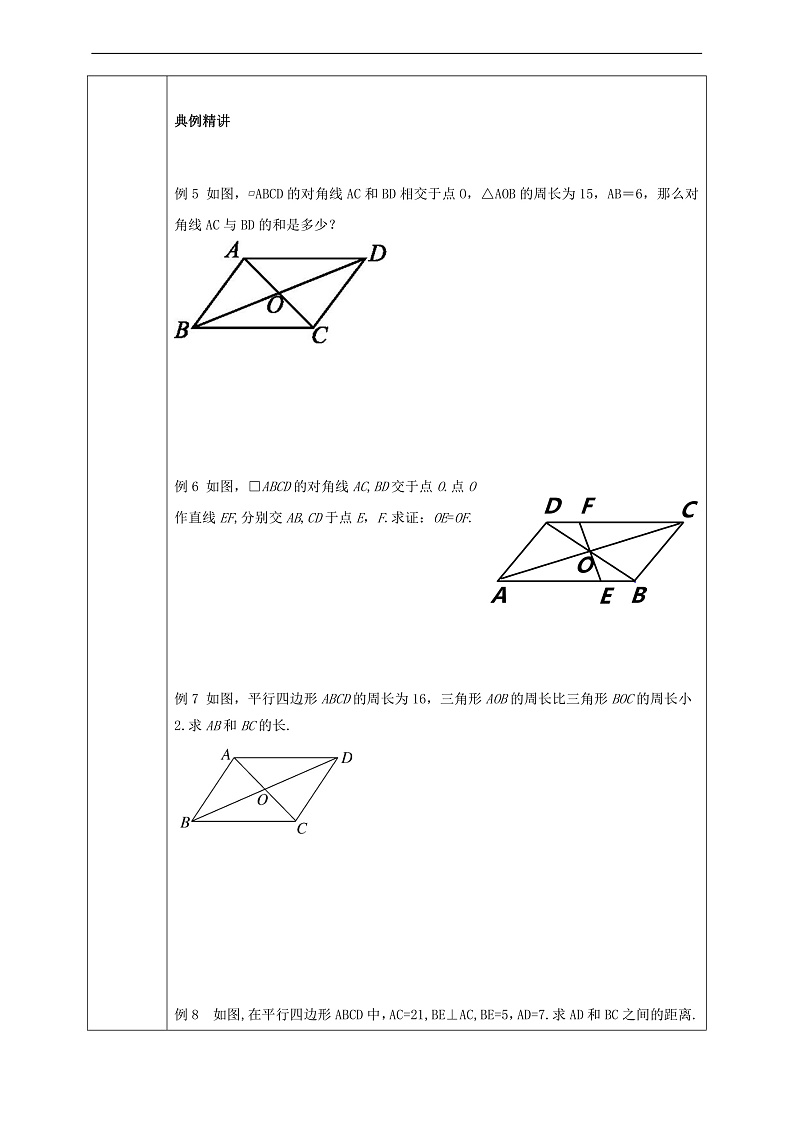
例5 如图□ ABCD的对角线AC和 BD相交于点O，△AOB的周长为15，AB=6，那么对角线AC与BD的和是多少？
解：在□ ABCD中∵∴AB=6，AO+BO+AB=15，∴AO+BO=15-6=9．又∵AO=OC，BO=OD(平行四边形对角线互相平分），∴AC+BD=2AO+2BO=2(AO+BO)=9×2=18．
例6 如图□ ABCD的对角线AC和BD相交于点O，EF过点O且与AB，CD相交于点E和点F．求证：OE=OF．
解：∵ABCD是平行四边形，∴OB=OD(平行四边形对角线互相平分）．又∵AB∥CD，∴∠EBO=∠FDO．又∵ ∠EBO=∠DOF，∴△BEO≌△DFO．∴OE=OF．
分析：要证明OE=OF，只要证明它们所在的两个三角形全等即可．
例7 如图□ ABCD的对角线AC与BD相交于点O，其周长为16，且△AOB的周长比△BOC的周长小2．求边AB和BC的长．
解：∵四边形ABCD是平行四边形，∴OA=OC(平行四边形对角线互相平分）．∵ △AOB的周+2= △BOC的周长，∴AO+BO+AB+2=BO+CO+BC，即 AB+2=BC．又∵ □ ABCD的周长=16，∴2（AB+BC)=16，即4AB+4=16．∴AB=3，BC=5．
例8 如图，在□ ABCD中，对角线AC=21cm，BE⊥AC，垂足为E ，且BE=5cm，AD=7cm．求AD和BC之间的距离．
解：设AD和BC之间的距离为x cm ，则□ ABCD的面积等于AD·x．
∴AD·x=AC·BE，即7x=21×5，x=15(cm)，即AD和BC之间的距离为15cm．
在应用平行四边形的性质时，我们应从三个方面去考虑：从边、角、对角线看它们的性质；从“平行四边形的对角线互相平分”中得出“平行四边形被它的两条对角线分成四个小三角形，相邻两个三角形的周长之差等于平行四边形的两邻边之差”；熟记这些结论，能为计算带来很多方便．
1.如图，□ABCD的对角线AC、BD相交于点O，且AC+BD=16，AD=6，则△BOC的周长是（ ）
A、10 B、14C、20 D、22
2.若平行四边形的对角线长分别为x和y，一边长为12，则x和y的值可能是（ ）A、8和14 B、10和14 C、18和20 D、10和36
3.如图，□ABCD的对角线AC与BD相交于点O，其周长为16，且△AOB的周长比△BOC的周长小2.求边AB和BC的长.
解：∵四边形ABCD是平行四边形∴AO=OC∵△AOB比△BOC周长小2∴AB+2=BC∵四边形ABCD周长为16，∴AB=3,BC=5
4.如图，在□ABCD中，O是对角线AC、BD的交点，BE⊥AC，DF⊥AC，垂足分别为点E、F.求证：OE=OF.
证明：∵平行四边形ABCD的对角线AC、BD交于一点O，∴OD=OB∵BE⊥AC，DF⊥AC∴∠AFD=∠CEB=90°又∵∠DOF=∠BOE∴△ODF≌△OBE∴OF=OE
平行四边形对角线的性质
平行四边形对角线互相平分
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交，得到的线段总相等.
1.□ABCD的对角线AC、BD相交于点O，AC=8，BD=6，AD=a,则a的取值范围是 ；
2.如图，在□ABCD中，EF过对角线的交点O，且与边AB、CD分别相交于点E、F，AB=4，AD=3,OF=1.3.求四边形BCFE的周长.
解：∵平行四边形ABCD的对角线交于点O， ∴BO=OD，AB//DC ∴∠EBO=∠FDO 又∠EOB=∠FOD ∴△BOE≌△DOF ∴BE=DF ∴四边形BCFE的周长=CD+BC+2OF=9.6
3. 如图，已知▱ABCD与▱EBFD的顶点A，E，F，C在一条直线上，求证：AE＝CF.
证明：如图，连结BD交AC于点O.∵四边形ABCD是平行四边形，∴OA＝OC(平行四边形的对角线互相平分)．∵四边形EBFD是平行四边形，∴OE＝OF(平行四边形的对角线互相平分)，∴OA－OE＝OC－OF，即AE＝CF(等式的性质)．