人教A版 (2019)选择性必修 第一册1.2 空间向量基本定理课文ppt课件

这是一份人教A版 (2019)选择性必修 第一册1.2 空间向量基本定理课文ppt课件，共26页。PPT课件主要包含了空间向量基本定理，问是否一定能做到，问如何进行表示，答综合几何方法，①适当选取基底，向量方法，课堂小结等内容，欢迎下载使用。
年 级：高二 学 科：数学（人教A版）主讲人：王琦 学 校：北京市第五中学
空间向量基本定理（2）
问题1 你能用自己的语言复述空间向量基本定理吗？
我们把{a，b，c}叫做空间的一个基底(base)，a，b，c 都叫做基向量(base vectrs) .
　　如果三个向量 a，b，c 不共面，那么对任意一个空间向量 p，存在唯一的有序实数组 (x，y，z)，使得p＝xa＋yb＋zc.
特别地，如果空间的一个基底中的三个基向量两两垂直，且长度都为1，那么这个基底叫做单位正交基底，常用{i，j，k}表示．
把一个空间向量分解为三个两两垂直的向量，叫做把空间向量进行正交分解．
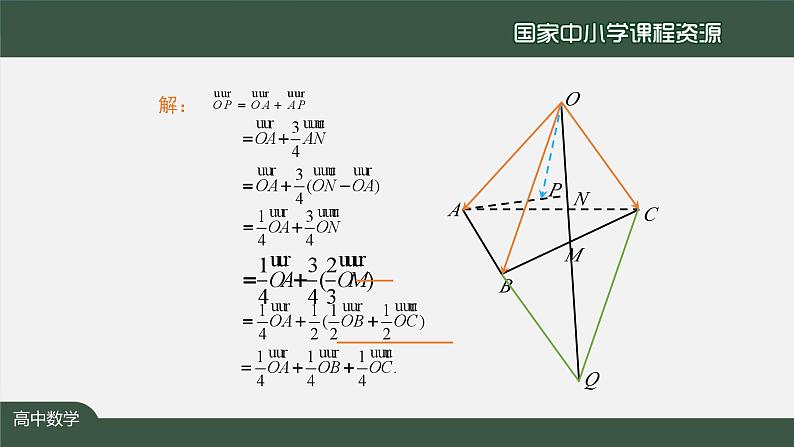
例1 如图，M 是四面体 OABC 的棱 BC 的中点，点 N 在线段 OM 上，点 P 在线段 AN 上，且 ， ，用向量 表示
空间向量基本定理保证了可行性．
可以构成空间的一个基底．
答：可以利用向量线性运算的 运算法则，如三角形法则、 平行四边形法则等．
问题2 通过这道例题的解题过程，同学们能否总结出用基向量表示空间向量的方法呢？
结合图形特征，利用三角形法则、平行四边形法则、向量数乘等线性运算法则，将待求向量逐步转化为基向量，将未知化归为已知.
用基向量表示空间向量的方法
问：证明异面直线垂直，你能想到 哪些方法？
证明异面直线所成角为直角；
线面垂直的定义和性质等．
例2 如图，在平行六面体 ABCD－A1B1C1D1中，AB＝4，AD＝4， AA1＝5，∠DAB＝60°，∠BAA1＝60 ° ，∠DAA1＝60 ° ，M，N 分别为D1C1，C1B1的中点． 求证 MN⊥AC1．
答：可以转化为向量问题
问：如何使用向量方法解决立体几何 问题？
这三个向量不共面，{a，b，c}是空间的一个基底．
则
所以
所以
选取基底(不共面且已知长度夹角)
把相关向量的运算转化为基向量的运算
用向量方法解决立体几何问题的路径
②用基向量表示相关向量
③将相关向量的问题转化为基向量的问题
理论基础：空间向量基本定理
答：可以取单位正交基底．
例3 如图，正方体 ABCD－A'B'C'D'的棱长为1，E，F， G分别为C'D'， A'D'， D'D的中点． （1）求证：EF∥AC ;
问：单位正方体这个条件对解题 有什么作用？
单位：基向量长度为1．
正交：基向量两两垂直，
任意两不同基向量数量积为0．
问：如何用向量方法证明EF//AC？
则 {i，j，k} 构成空间的一个单位正交基底．
问：如何用向量表示 CE 与 AG 所 成角的余弦值？
例3 如图，正方体 ABCD－A'B'C'D'的棱长为1，E，F， G分别为C'D'， A'D'， D'D的中点． （1）求证：EF∥AC ; （2）求 CE 与 AG 所成角 的余弦值．
因为
1
0
思考：是否可以用 与 所成角的余弦值来求解第2小问？
应用一个定理：空间向量基本定理 学习一种方法：向量方法 体会一种思想：转化与化归思想