2024-2025学年上海市复兴中学高一（上）数学期末试卷+答案

这是一份2024-2025学年上海市复兴中学高一（上）数学期末试卷+答案，共20页。
10．已知直线是抛物线的准线，抛物线的顶点为原点，焦点为，若为上一点，与的对称轴交于点，在中，，则的值为 .
11．阅读材料：空间直角坐标系中，过点且一个法向量为的平面的方程为．
阅读上面材料，解决下面问题：已知平面的方程为，直线是两平面与的交线，则直线与平面所成角的正弦值为 .
12．在三棱锥中，，且，则二面角的余弦值的最小值为 .
二、选择题（本大题共4题，满分18分.其中第13-14题4分，第15-16题5分）.
13．数学家欧拉在1765年发现，任意三角形的外心，重心，垂心位于同一条直线上，这条直线称为三角形欧拉线.已知的顶点坐标为，则欧拉线的方程为（ ）.
A． B．
C． D．
14．沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时．如图，某沙漏由上下两个圆道组成，圆锥的底面直径和高均为8cm，细沙全部在上部，其高度为圆锥高度的（细管长度忽略不计）.假设该沙漏每秒钟漏下的沙，则该沙漏的一个沙时大约是（ ）（.
A．1895秒 B．1896秒
C．1985秒 D．2528秒
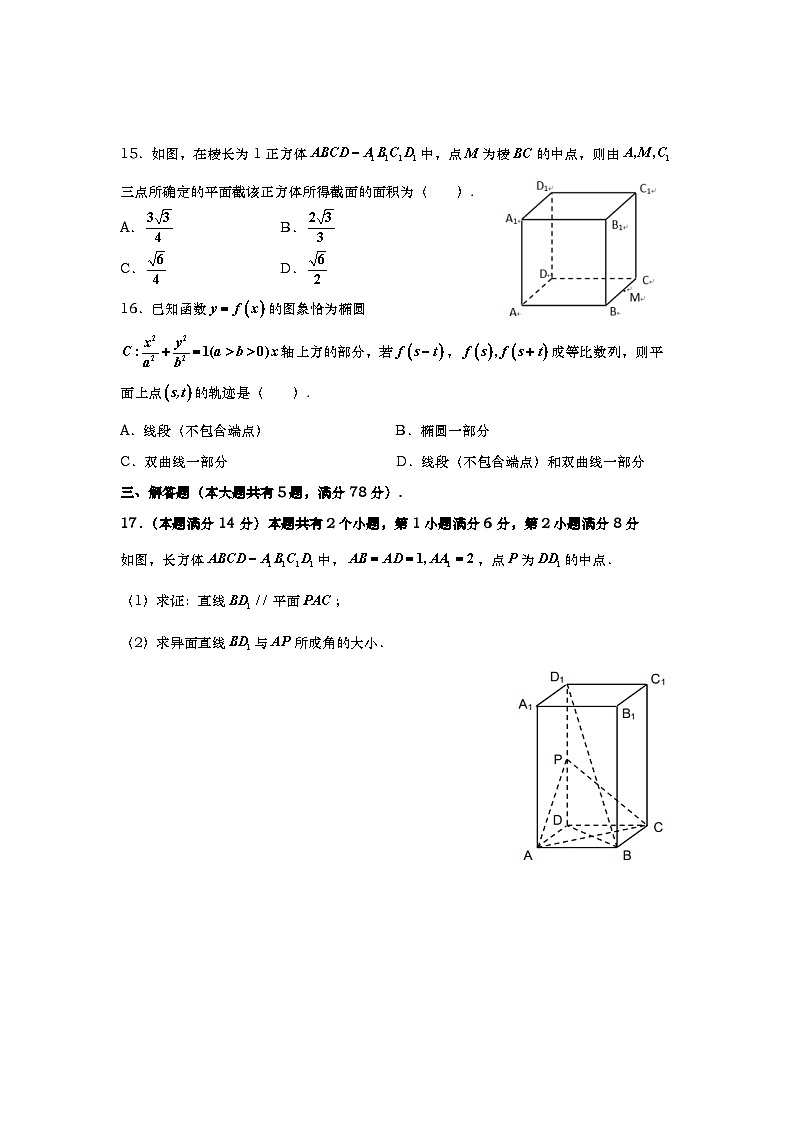
15．如图，在棱长为1正方体中，点为棱的中点，则由三点所确定的平面截该正方体所得截面的面积为（ ）.
A． B．
C． D．
16．已知函数的图象恰为椭圆轴上方的部分，若，成等比数列，则平面上点的轨迹是（ ）.
A．线段（不包含端点） B．椭圆一部分
C．双曲线一部分 D．线段（不包含端点）和双曲线一部分
三、解答题（本大题共有5题，满分78分）.
17．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分
如图，长方体中，，点为的中点．
（1）求证：直线平面；
（2）求异面直线与所成角的大小．
18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分
已知圆，直线．
（1）证明：不论取什么实数，直线与圆恒相交于两点；
（2）直线能否将圆分割成弧长的比值为的两段圆弧？为什么？
19．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分
已知双曲线的左，右焦点分别为．
（1）若的实轴长为2，焦距为4，求的渐近线方程：
（2）已知是双曲线的左支上一点，）.当周长最小时，求的面积．
20．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分
如图，在四棱锥中，底面是等腰梯形，，平面平面．
（1）求证：；
（2）求证：为直角三角形；
（3）若，求四棱棱的体积．

21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题的①满分6分，第2小题的②满分8分
已知为抛物线的焦点，过点的直线与抛物线相交于（）两点．
（1）证明：是常数；
（2）过点作直线的垂线与抛物线的准线相交于点，与抛物线相交于两点（点的横坐标小于点的横坐标）.
①求的值；
②是否存在最小值？若存在，请求出这个最小值；若不存在，请说明理由．
复兴中学2024学年第一学期高二年级数学期末
2025.1
一、填空题（本大题共有12题,满分54分,第1-6题每题4分,第7-12题每题5分）
1．直线的倾斜角为 .
【答案】
2．平行于同一平面的两直线的位置可能是 .
【答案】平行或相交或异面
3．已知圆锥的母线与底面所成角为，高为1，则该圆锥的母线长为 .
【答案】
4．经过点且与圆相切的直线方程是 .
【答案】
5．一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为，则此球表面积为 .
【答案】
6．如图，在长方体中，棱，，则直线到平面的距离为 .
【答案】
7．已知平行直线和的距离为，则 .
【答案】6或8
8．已知双曲线，若椭圆以双曲线的顶点为焦点，长轴长为，则椭圆的标准方程为 .
【答案】
9．如图，是底面半径为的圆柱侧面上两点，它们在底面上的射影分别为，若，弧，则沿圆柱侧面从到的最短距离是 .
【答案】
10．已知直线是抛物线的准线，抛物线的顶点为原点，焦点为，若为上一点，与的对称轴交于点，在中，，则的值为 .
【答案】
11．阅读材料：空间直角坐标系中，过点且一个法向量为的平面的方程为．
阅读上面材料，解决下面问题：已知平面的方程为，直线是两平面与的交线，则直线与平面所成角的正弦值为 .
【答案】0
【解析】平面的方程为，可得平面的法向量为，
平面的法向量为的法向量为，
设直线的方向向量为，则，即，
令，则，设直线与平面所成角，
则，所以直线与平面所成角的正弦值为0．
12．在三棱锥中，，且，则二面角的余弦值的最小值为 .
【答案】
【解析】因为，所以，点的轨迹方程为（椭球），
又因为，所以点A的轨迹方程为，（双曲线的一支）．
过点作，而面，所以面，
设为中点，则二面角为，直角坐标系内
设点为焦点，则点的轨迹为椭圆方程为，
点的轨迹为双曲线一支方程为，
过点作交于点，连接，将面沿直线折成二面角，
则为二面角的平面角．
设点横坐标为，则，则，
于是可得：
由于，得．
二、选择题（本大题共4题，满分18分.其中第13-14题4分，第15-16题5分）.
13．数学家欧拉在1765年发现，任意三角形的外心，重心，垂心位于同一条直线上，这条直线称为三角形欧拉线.已知的顶点坐标为，则欧拉线的方程为（ ）.
A． B． C． D．
【答案】A
14．沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时．如图，某沙漏由上下两个圆道组成，圆锥的底面直径和高均为8cm，细沙全部在上部，其高度为圆锥高度的（细管长度忽略不计）.假设该沙漏每秒钟漏下的沙，则该沙漏的一个沙时大约是（ ）（.
A．1895秒 B．1896秒
C．1985秒 D．2528秒
【答案】C
15．如图，在棱长为1正方体中，点为棱的中点，则由三点所确定的平面截该正方体所得截面的面积为（ ）.
A． B．
C． D．
【答案】D
16．已知函数的图象恰为椭圆轴上方的部分，若，成等比数列，则平面上点的轨迹是（ ）.
A．线段（不包含端点） B．椭圆一部分
C．双曲线一部分 D．线段（不包含端点）和双曲线一部分
【答案】A
【解析】因为函数的图象恰为椭圆轴上方的部分，
所以，因为成等比数列，
所以有，且有成立，
即成立，
由，
化简得：，或，
当时，即，因为，所以平面上点（）的轨迹是线段（不包含端点）；
当时，即，因为，所以，
而，所以不成立，故选：A
三、解答题（本大题共有5题，满分78分）.
17．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分
如图，长方体中，，点为的中点．
（1）求证：直线平面；
（2）求异面直线与所成角的大小．
【答案】（1）见解析 （2）
【解析】（1）证明：设和交于点，则为的中点，连结，又∵是的中点，∴，
又∵平面平面直线平面．
（2）由（1）知：，∴为异面直线与所成的角（或其补角）
∵且，
∴，即异面直线与所成角的大小为．
18．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分
已知圆，直线．
（1）证明：不论取什么实数，直线与圆恒相交于两点；
（2）直线能否将圆分割成弧长的比值为的两段圆弧？为什么？
【答案】（1）见解析 （2）能，理由见解析
【解析】（1）直线，即，
由，解得，故直线过定点，
又因为，故点在圆内，则直线与圆C恒相交两点，
（2）设直线与圆C相交于，假设直线能将圆C分割成弧长的比值为的两段圆弧，则圆心角，即点C到直线的距离为化简得，所以，所以存在直线满足题意.
（或者利用此时，此时即过垂直于的直线满足题意）
19．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分
已知双曲线的左，右焦点分别为．
（1）若的实轴长为2，焦距为4，求的渐近线方程：
（2）已知是双曲线的左支上一点，）.当周长最小时，求的面积．
【答案】（1） （2）
【解析】（1）令双曲线的半焦距为，依题意，，由，得，
则，所以双曲线的渐近线方程为．
（2）由双曲线的定义可得，
所以的周长为，
由于为定值，要使的周长最小，则应使最小为，
即点在线段上∵，所以直线的方程为：，
即，将其代入，解得或（舍去），因此点.所以
20．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分
如图，在四棱锥中，底面是等腰梯形，，平面平面．
（1）求证：；
（2）求证：为直角三角形；
（3）若，求四棱棱的体积．
【答案】（1）见解析 （2）见解析 （3）
【解析】（1）证明：作为垂足，在等腰梯形ABCD中，设，
所以，
故，所以，所以
（2）因为，平面平面，平面平面平面，平面平面∵平面
平面平面，∴，即为直角三角形
（3）由（1）知在等腰梯形ABCD中，，∴，
又平面为直角三角形，
∴，
而．
21．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题的①满分6分，第2小题的②满分8分
已知为抛物线的焦点，过点的直线与抛物线相交于（）两点．
（1）证明：是常数；
（2）过点作直线的垂线与抛物线的准线相交于点，与抛物线相交于两点（点的横坐标小于点的横坐标）.
①求的值；
②是否存在最小值？若存在，请求出这个最小值；若不存在，请说明理由．
【答案】（1）见解析 （2）① ②存在，最小值为48.
【解析】（1）由已知，点的坐标为，且可设直线的方程为，
联立方程组，消去，得，
因为，
所以为方程（＊）的两个实根，且，
因为点在抛物线上，所以，为常数．
（2）在题设条件下，直线都不与坐标轴平行且，
由（1）可知直线的方程为：，
①因为抛物线的准线方程为，代入的方程可得点的坐标为，
由（1）可知，，
因此，分）
即．
另解：设在准线上的射影分别为，则
由抛物线定义可知，又，则Rt则，
同理，可得则
②存在最小值，
设点的坐标分别为，
因为点均在抛物线上，所以，
由，有，即，
变形可得，则，
同理，分）
根据抛物线的定义可知，
，
所以
由（＊＊）知，，即，
当且仅当时取＂，同理，，当且仅当时取＂，
由题设，，所以，
所以，
由题意可知，同时成立，
此时，取得最小值，
故存在最小值，最小值为48.
另解：存在最小值，
假设直线的倾斜角为，根据题意可设，如图，设点在轴上的射影为点，
抛物线的准线与轴相交于点，
根据抛物线的定义，由题设点的位置可知
同理可得，，
所以
令，
则，（15分）
由，可得，易知函数为增函数，
所以，上式中，当且仅当，即时（此时）等号成立，所以，，
所以，存在最小值48，该最小值当且仅当时取得．（18分）
另法：不妨设，如图直线为
,
由于显然
直线为，同理可得
则
显然，而函数在上为严格增函数
则即时，