北师大版（2024）七年级下册（2024）1 两条直线的位置关系课前预习课件ppt

这是一份北师大版（2024）七年级下册（2024）1 两条直线的位置关系课前预习课件ppt，共24页。PPT课件主要包含了垂直的定义，垂直的表示方法，探究二垂线的画法，可以画无数条，放2靠3画，可以画一条，垂线的性质1，线段PO最短，垂线的性质2，点到直线的距离等内容，欢迎下载使用。
1. 了解垂线的有关概念、性质及画法，了解点到直线的距离的概念；（重点）2. 能够运用垂线的有关性质进行运算，并解决实际问题.（难点）
日常生活中，如图中的两条直线的关系很常见，你能再举出其他例子吗？
想一想：两条相交直线在什么情况下是垂直的？
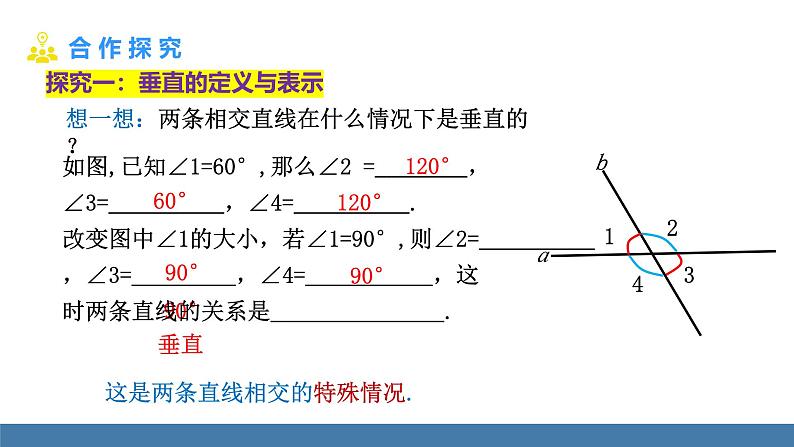
这是两条直线相交的特殊情况.
探究一：垂直的定义与表示
如图,已知∠1=60°,那么∠2 = ，∠3= ，∠4= .改变图中∠1的大小，若∠1=90°,则∠2= ，∠3= ，∠4= ，这时两条直线的关系是 .
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直,其中一条直线叫作另一条直线的垂线，它们的交点叫做垂足.
垂直是两直线相交的一种特例.
☀注意：(1)线段与线段、线段与射线、射线与射线、线段与直线、射线与直线垂直,指它们所在的直线互相垂直;(2)两条直线互相垂直,则形成的四个角为直角.反之,要说明两条直线垂直,只要说明这两条直线相交成的角中有一个角为直角即可.
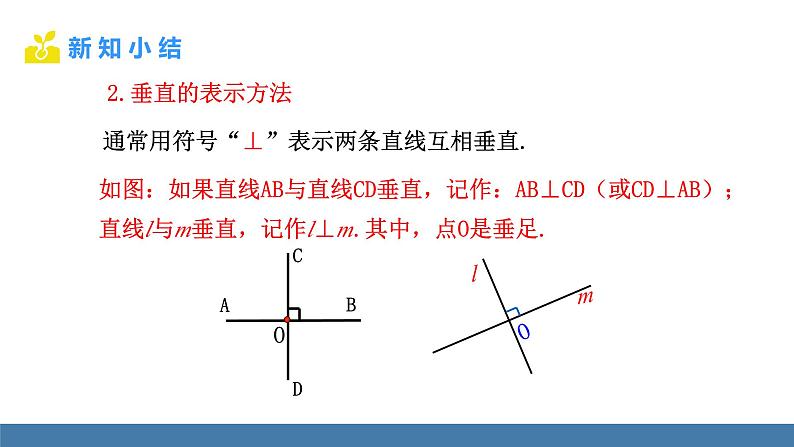
通常用符号“⊥”表示两条直线互相垂直.
如图：如果直线AB与直线CD垂直，记作：AB⊥CD（或CD⊥AB）；直线l与m垂直，记作l⊥m.其中，点O是垂足.
解：CE⊥CD，理由如下：∵∠ACE=31°，∠DCB=59°,∴∠ECD=180°-∠ACE-∠DCB =180°-31°-59° =90°.∴CE⊥CD.
例1 如图，C为直线 AB上一点，过点C引两条射线 CE，CD，且∠ACE=31°，∠DCB=59°.那么CE，CD的位置关系是什么?为什么?
(1)如图,O为直线AB上一点，∠AOC＝∠BOC，那么OC与AB垂直吗？为什么？
由∠AOC＝∠BOC，且∠AOC+∠BOC＝180°，可得∠AOC＝∠BOC=90°，所以OC⊥AB.
(2)以下是小颖的思考过程，她的想法正确吗？你知道她每一步的依据吗?与同伴进行交流.
(3)如果OC⊥AB，那么∠AOC＝∠BOC吗？
因为OC⊥AB，所以∠AOC＝∠BOC=90°.
(1)你能用折叠的方法折出互相垂直的直线吗？试试看！
(2)如果只有直尺，你能在方格纸上画出已知直线的垂线吗？你还能再画出两条互相垂直的直线吗？
画已知直线的垂线有三种方法：(1)用三角尺画垂线;(2)用量角器画垂线;(3)借助网格纸画垂线.
例2 下列各图中,过直线l外的点P画直线l的垂线,三角尺操作正确的是 (　　)
探究三：垂线的性质和点到直线的距离
做一做：(1)画已知直线l的垂线能画几条?
(2)如图，点A在直线l上, 过点A画直线l的垂线，你能画出多少条?
1.放2.靠3.移4.画
(3)如图，点A在直线l外, 过点A画直线l的垂线，你能画出多少条呢?
根据以上操作，你能得出什么结论
同一平面内，过一点有且只有一条直线与已知直线垂直.
☀注意：1.“过一点”中的点，可以在已知直线上，也可以在已知直线外；2.“有且只有”中，“有”指存在，“只有”指唯一性.
（4）如图所示，P是直线l外一点,PO⊥l,点O是垂足.点A,B,C在直线l上,比较线段PO,PA,PB,PC的长短,你发现了什么?
直线外一点与直线上各点连接的所有线段中，垂线段最短.简单说成：垂线段最短.
如图所示，过点A作直线l的垂线,垂足为B,线段AB的长度叫做点A到直线l的距离.
例3 如图所示，在三角形ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=4 cm,BC=3 cm,AB=5 cm,则点A到直线BC的距离为　　　　cm,点B到直线AC的距离为　　　　cm,点C到直线AB的距离为　　　　cm. 
解析：点到直线的距离是该点到这条直线的垂线段的长度,而垂线段是该点与直线上各点的连线中最短的,从条件看,PC是三条线段中最短的,但不一定是所有线段中最短的,所以点P到直线m的距离应该是不大于2cm.
例4 P为直线m外一点，A,B,C为直线m上的三点，PA=4cm，PB=5cm，PC=2cm,则点P到直线m的距离 (　　)A.等于4cmB.等于2cmC.小于2cmD.不大于2cm
2.P为直线l外一点,A,B,C为直线l上的三点,PA=3 cm,PB=4 cm, PC=5 cm,则点P到直l的距离(　　)A.等于2 cmB.等于3 cmC.小于3 cmD.不大于3 cm
1.如图所示，直线AB，CD相交于点O，下列条件中，不能说明AB⊥CD的是(　　)A.∠AOD=90° B.∠AOC=∠BOCC.∠BOC+∠BOD=180° D.∠AOC+∠BOD=180°
3.如图所示,已知点O在直线AB上,CO⊥DO.若∠1=155°,则∠3的度数为　 . 
4.如图所示，单位要在河岸l上建一个水泵房引水到C处.他们的做法是:过点C作CD⊥l于点D,将水泵房建在了D处.这样做最节省水管,其数学道理是　　　 　　　. 
解:如图,过点A画CB的垂线,交CB的延长线于点E.
根据点到直线的距离的定义:从直线外一点到这条直线的垂线段的长度,叫这点到这条直线的距离.可得AE的长度即为点A到直线CB的距离.
5.如图所示，过点A画CB的垂线,并指出哪条线段的长度表示点A到直线CB的距离.
解:∵AB⊥CD,∴∠COB=90°.∴∠EOB=90°-∠COE=90°-35°=55°.∴∠BOF=180°-∠EOB=180°-55°=125°.故∠EOB的度数是55°,∠BOF的度数是125°.
6.如图所示，直线AB，CD，EF都经过点O，且AB⊥CD，∠COE=35°，求∠EOB，∠BOF的度数.