高中湘教版（2019）1.1 导数概念及其意义教学课件ppt

这是一份高中湘教版（2019）1.1 导数概念及其意义教学课件ppt，共23页。PPT课件主要包含了x0+Δx，曲线的切线，导数的几何意义，思考3，圆的周长公式，以直代曲，又切线的斜率为1，所以3x021，求切线的斜率的步骤，课堂小结等内容，欢迎下载使用。
通过函数的图象直观地理解导数的几何意义并会用导数的几何意义求函数图象的切线
体会“无限逼近”、“以直代曲”的数学思想
理解曲线的切线的概念；通过函数的图象直观地理解导数的几何意义并会用导数的几何意义求函数图象的切线；体会“无限逼近”、“以直代曲”的数学思想。
运动员的运动轨迹是抛物线，其速度方向是时刻变化的，其在2s时刻的瞬时速度的方向线是抛物线的切线
如何求抛物线的切线斜率？如何求曲线的切线斜率？
请说出函数y=f(x在区间[x0, x0+Δx]上的平均变化率，及其几何意义
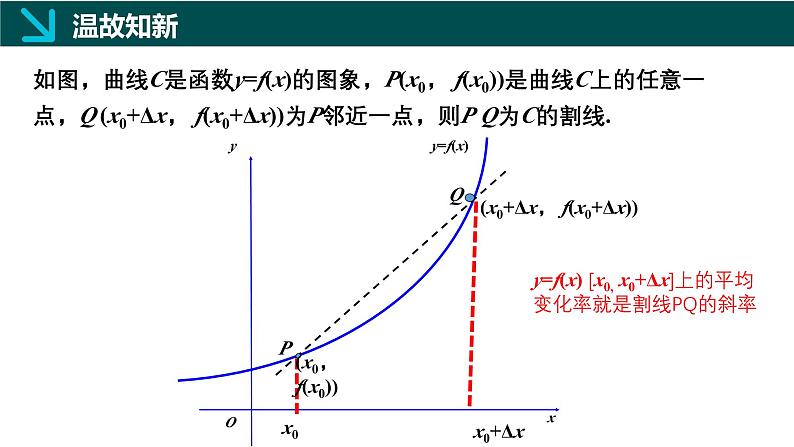
如图，曲线C是函数y=f(x)的图象，P(x0， f(x0))是曲线C上的任意一点，Q (x0+Δx， f(x0+Δx))为P邻近一点，则P Q为C的割线.
(x0， f(x0))
(x0+Δx， f(x0+Δx))
y=f(x) [x0, x0+Δx]上的平均变化率就是割线PQ的斜率
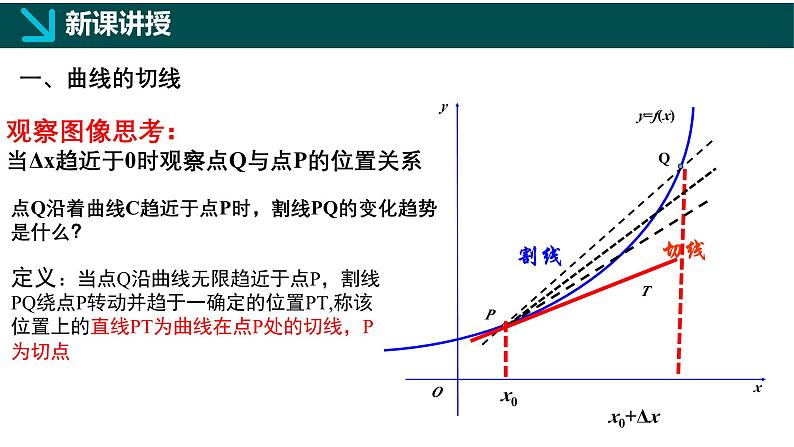
观察图像思考：当Δx趋近于0时观察点Q与点P的位置关系
点Q沿着曲线C趋近于点P时，割线PQ的变化趋势是什么？
定义：当点Q沿曲线无限趋近于点P，割线PQ绕点P转动并趋于一确定的位置PT,称该位置上的直线PT为曲线在点P处的切线，P为切点
思考1：割线PQ的斜率如何计算？
思考2：根据割线与切线的关系，切线PT的斜率k如何计算？
函数 y=f(x) 在点x0处的导数f‘(x0)的几何意义是：
故曲线 y=f(x) 在点P(x0，f(x0))处的切线方程为：
若曲线y=f(x)在点P(x0，f(x0))处的导数f ′(x0)不存在，则该曲线在点P处的切线与y轴平行，即切线的倾斜角为直角.
思考1：若函数 y=f(x) 在点P(x0，f(x0))处的导数 f'(x0) 不存在，则函数的切线有什么特点？
思考2：那 f'(x0)=0，f'(x0)>0，f'(x0)0，切线的倾斜角为锐角； f ′(x0)