初中人教版（2024）17.1 勾股定理一课一练

这是一份初中人教版（2024）17.1 勾股定理一课一练，文件包含第十七章《勾股定理》单元检测解答doc、第十七章《勾股定理》单元检测doc等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。
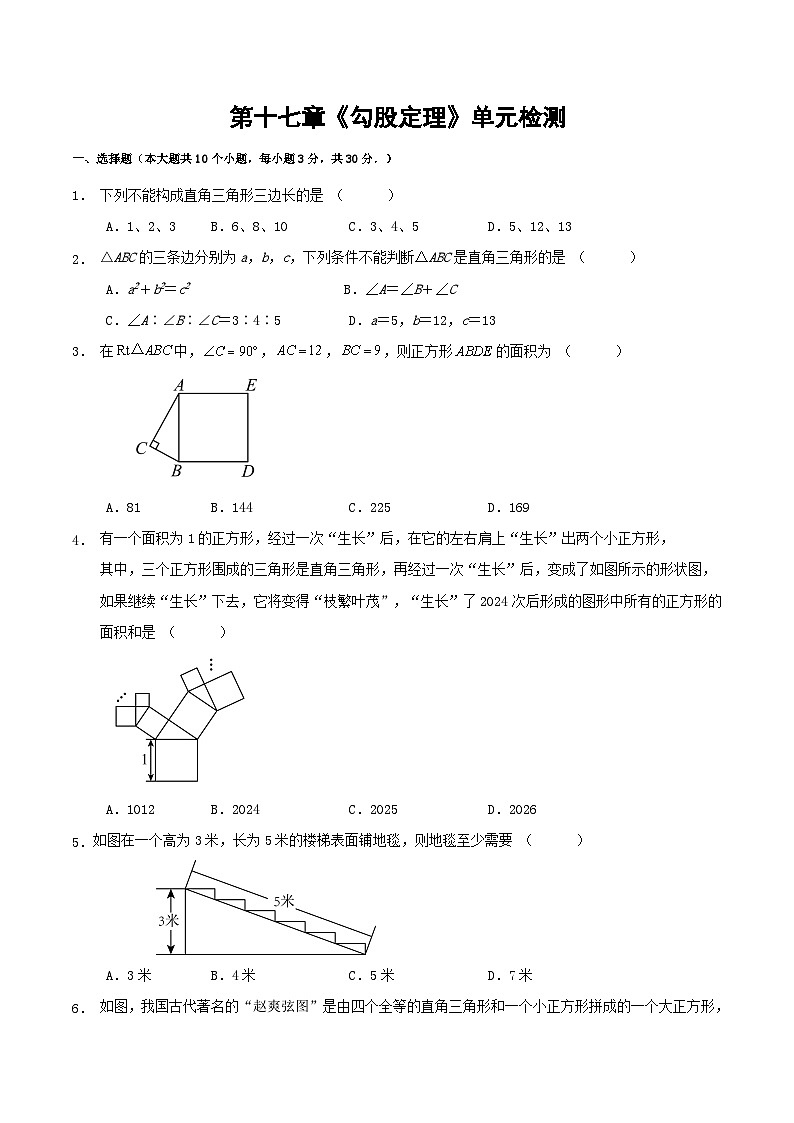
1． 下列不能构成直角三角形三边长的是 （ ）
A．1、2、3B．6、8、10C．3、4、5D．5、12、13
△ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是 （ ）
A．a2＋b2＝c2 B．∠A＝∠B＋∠C
C．∠A∶∠B∶∠C＝3∶4∶5D．a＝5，b＝12，c＝13
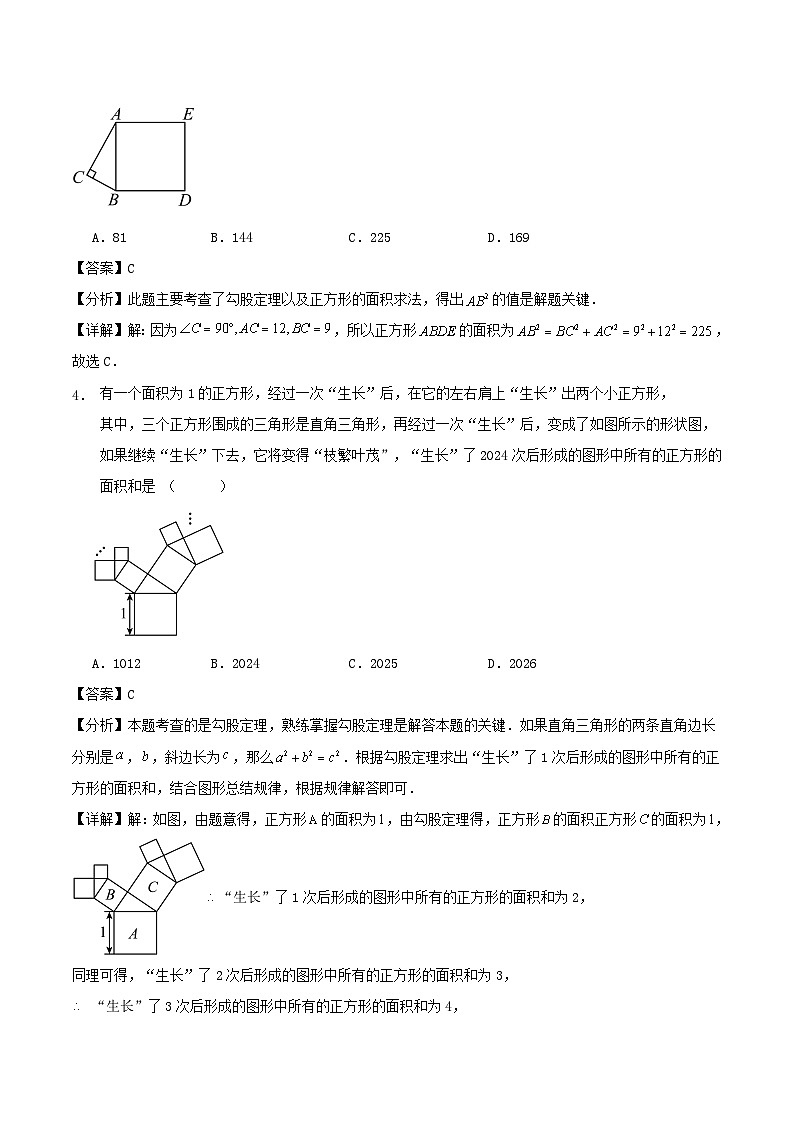
3． 在中，，，，则正方形的面积为 （ ）

A．81B．144C．225D．169
有一个面积为1的正方形，经过一次“生长”后，在它的左右肩上“生长”出两个小正方形，
其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了如图所示的形状图，
如果继续“生长”下去，它将变得“枝繁叶茂”，“生长”了2024次后形成的图形中所有的正方形的
面积和是 （ ）

A．1012B．2024C．2025D．2026
如图在一个高为3米，长为5米的楼梯表面铺地毯，则地毯至少需要 （ ）

A．3米B．4米C．5米D．7米
如图，我国古代著名的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，
设直角三角形的较短直角边为，较长直角边为，若，大正方形的面积为34，
则小正方形的面积为 （ ）

A．1B．2C．4D．8
如图，在底面周长约为6米且带有层层回环不断的云朵石柱上，
有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方（从点到点，为的中点），
每根华表刻有雕龙的部分的柱身高约16米，则雕刻在石柱上的巨龙的长度至少为 （ ）

A．10米B．12米C．16米D．20米
如图，从点发出一束光，经轴反射，过点，
则这束光从点到点所经过的路径的长为（ ）

A．B．C．D．
9 . 中国古代的数学家们不仅很早就发现并应用勾股定理，而且很早就尝试对勾股定理作理论的证明．
最早对勾股定理进行证明的，是三国时期吴国的数学家赵爽．赵爽创制了一幅“勾股圆方图”，
用形数结合得到方法，给出了勾股定理的详细证明．如图，已知大正方形面积为64，
中心小正方形面积为16，若用m，n表示直角的两条直角边，下列四个说法：
①，②，③，④．其中说法正确的是（ ）

A．①B．①②C．①②③D．①②③④
10． 我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式，后人借助这种分割方法所得的图形证明了勾股定理．
如图所示的矩形由两个这样的图形拼成，若，，则该长方形的面积为（ ）

A．20B．18C．D．
二、填空题：（本大题共8个小题，每小题3分，共24分．）
11 . 如图，一次飓风灾害中，一棵大树在离地面3米处折断，树的顶端落在离树杆底部4米处，
那么这棵树折断之前的高度是_____

12 . 如图是北京第24届国际数学家大会会徽，由4个全等的直角三角形拼合而成，
若图中大小正方形的面积分别为13和1，且直角三角形的两直角边分别为a，b，
则的值为 ．

如图，四边形中，，，，，则的长为 ．

如图，《九章算术》中有这样一道古题：今有一竖直着的木柱，在木柱的上端系有绳索，
绳索从木柱的上端顺木柱下垂后堆在地面的部分有四尺（绳索比木柱长4尺），牵着绳索退行，
在距木柱底部8尺处时而绳索用尽，则木柱长为 尺．

以下有一首古算诗，根据诗中的描述可以计算出红莲所在位置的湖水深度，其示意图如图，
其中，于点，尺，尺．则的长度为 尺．

如图，折叠长方形一边，使D落在边的点F处，
已知，，则的长 ．
．
如图，有一张直角三角形纸片，两直角边，，现将折叠，
使点与点重合，得到折痕，则的面积为 ．

小明在公园里荡秋千．如图，小明坐在秋千的起始位置A处，荡绳与地面垂直，
荡至右侧最高位置为，荡至左侧最高位置为．已知起始位置A离地面垂直距离为，
点B离地面垂直距离为．点B到的水平距离为，．
则点C离地面的垂直距离为 m．

三、解答题：（本大题共6个小题，共46分．解答应写出文字说明、证明过程或演算步骤．）
19． 求如图的Rt△ABC的面积．

20 . 如图是一个滑梯示意图，若将滑梯AC水平放置，则刚好与AB一样长．
已知滑梯的高度CE＝6m，CD＝2m，求滑道AC的长．

某数学兴趣小组开展了“笔记本电脑的顶部边缘离桌面的高度与用眼舒适度关系”的实践探究活动．
已知笔记本的宽度为，当顶部边缘A处离桌面的高度为时，
此时用眼舒适度不太理想．小组成员调整顶部边缘离桌面的高度，
最后发现当顶部边缘离桌面的高度时，用眼舒适度较为理想．
求调整前后顶部边缘移动的水平距离的长．

如图，在中，，，，D为上的一点，
将沿折叠，使点C恰好落在上的点E处．

(1)求的长．
(2)求的长．
小明在公园里荡秋千．如图，小明坐在秋千的起始位置处，与地面垂直，
两脚在地面上用力一蹬，在距地面高的处停止并回落，然后在处停止再回落．
若、到的水平距离、分别为和，．

(1)与全等吗？请说明理由．
(2) 秋千的起始位置处距地面是多高？
著名的赵爽弦图(如图①，其中四个直角三角形较大的直角边长都为，较小的直角边长都为，
斜边长都为)，大正方形的面积可以表示为，也可以表示为，
由此推导出重要的勾股定理：如果直角三角形两条直角边长为，，斜边长为，则．

【结论探究】
(1)图②为美国第二十任总统伽菲尔德的“总统证法”，请你利用图②推导勾股定理；
【结论应用】
如图③，在一条东西走向河流的一侧有一村庄，河边原有两个取水点，，
，由于某种原因，由到的路现在已经不通，
该村为方便村民取水决定在河边新建一个取水点，，在同一条直线上，
并新修一条路，且．测得千米，千米，
求新路比原路少多少千米？
【问题拓展】
中，，，，，垂足为，请直接写出的值．
诗文：
波平如镜一湖面，半尺高处生红莲
亭亭多姿湖中立，突遭狂风吹一边
离开原处二尺远，花贴湖面象睡莲