2025年中考数学一轮复习分层精练专题12 二次函数的图像与性质及与a、b、c的关系（2份，原卷版+解析版）

这是一份2025年中考数学一轮复习分层精练专题12 二次函数的图像与性质及与a、b、c的关系（2份，原卷版+解析版），文件包含2025年中考数学一轮复习分层精练专题12二次函数的图像与性质及与abc的关系原卷版doc、2025年中考数学一轮复习分层精练专题12二次函数的图像与性质及与abc的关系解析版doc等2份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。

1．（2022•哈尔滨）抛物线y＝2（x+9）2﹣3的顶点坐标是（ ）
A．（9，﹣3）B．（﹣9，﹣3）C．（9，3）D．（﹣9，3）
【答案】B
【解答】解：∵y＝2（x+9）2﹣3，
∴抛物线顶点坐标为（﹣9，﹣3），
故选：B．
2．（2022•黑龙江）若二次函数y＝ax2的图象经过点P（﹣2，4），则该图象必经过点（ ）
A．（2，4）B．（﹣2，﹣4）C．（﹣4，2）D．（4，﹣2）
【答案】A
【解答】解：∵二次函数y＝ax2的对称轴为y轴，
∴若图象经过点P（﹣2，4），
则该图象必经过点（2，4）．
故选：A．
3．（2021•兰州）二次函数y＝x2+4x+1的图象的对称轴是（ ）
A．x＝2B．x＝4C．x＝﹣2D．x＝﹣4
【答案】C
【解答】解：∵二次函数y＝x2+4x+1，
∴抛物线对称轴为直线x＝﹣＝﹣2．
故选：C．
4．（2022•新疆）已知抛物线y＝（x﹣2）2+1，下列结论错误的是（ ）
A．抛物线开口向上
B．抛物线的对称轴为直线x＝2
C．抛物线的顶点坐标为（2，1）
D．当x＜2时，y随x的增大而增大
【答案】D
【解答】解：A选项，∵a＝1＞0，
∴抛物线开口向上，故该选项不符合题意；
B选项，抛物线的对称轴为直线x＝2，故该选项不符合题意；
C选项，抛物线的顶点坐标为（2，1），故该选项不符合题意；
D选项，当x＜2时，y随x的增大而减小，故该选项符合题意；
故选：D．
5．（2022•荆门）抛物线y＝x2+3上有两点A（x1，y1），B（x2，y2），若y1＜y2，则下列结论正确的是（ ）
A．0≤x1＜x2B．x2＜x1≤0
C．x2＜x1≤0或0≤x1＜x2D．以上都不对
【答案】D
【解答】解：抛物线y＝x2+3开口向上，对称轴为y轴，
∵抛物线y＝x2+3上有两点A（x1，y1），B（x2，y2），且y1＜y2，
∴|x1|＜|x2|，
∴0≤x1＜x2或x2＜x1≤0或0＜﹣x1＜x2或0＜x1＜﹣x2，
故选：D．
6．（2022•宁波）点A（m﹣1，y1），B（m，y2）都在二次函数y＝（x﹣1）2+n的图象上．若y1＜y2，则m的取值范围为（ ）
A．m＞2B．m＞C．m＜1D．＜m＜2
【答案】B
【解答】解：∵点A（m﹣1，y1），B（m，y2）都在二次函数y＝（x﹣1）2+n的图象上，
∴y1＝（m﹣1﹣1）2+n＝（m﹣2）2+n，
y2＝（m﹣1）2+n，
∵y1＜y2，
∴（m﹣2）2+n＜（m﹣1）2+n，
∴（m﹣2）2﹣（m﹣1）2＜0，
即﹣2m+3＜0，
∴m＞，
故选：B．
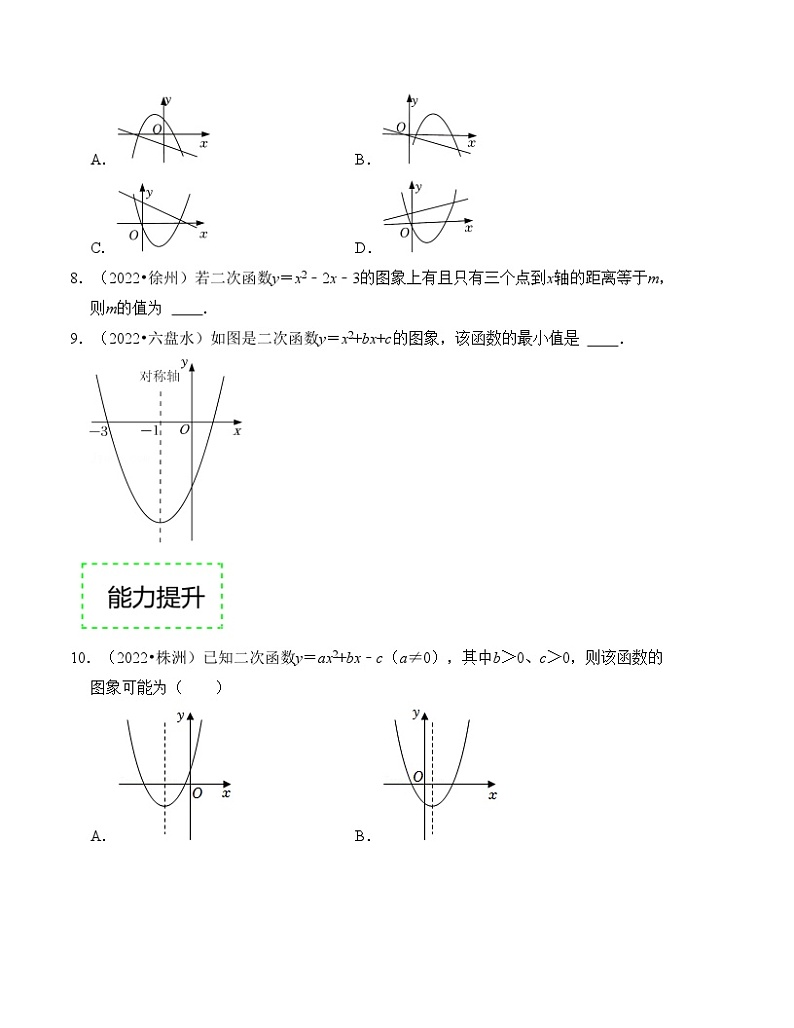
7．（2022•合肥模拟）二次函数y＝ax2﹣bx和一次函数y＝bx+a在同一平面直角坐标系中的图象可能是（ ）
A．B．
C．D．
【答案】D
【解答】A、由二次函数y＝ax2﹣bx可知，图象过原点，故本选项错误；
B、由二次函数y＝ax2﹣bx可知，图象过原点，故本选项错误；
C、由抛物线可知，a＞0，x＝﹣＞0，得b＞0，由直线可知，a＞0，b＜0，故本选项错误；
D、由抛物线可知，a＞0，x＝﹣＞0，得b＞0，由直线可知，a＞0，b＞0，故本选项正确．
故选：D．
8．（2022•徐州）若二次函数y＝x2﹣2x﹣3的图象上有且只有三个点到x轴的距离等于m，则m的值为 ．
【答案】4
【解答】解：∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
∴抛物线开口向上，抛物线对称轴为直线x＝1，顶点为（1，﹣4），
∴顶点到x轴的距离为4，
∵函数图象有三个点到x轴的距离为m，
∴m＝4，
故答案为：4．
9．（2022•六盘水）如图是二次函数y＝x2+bx+c的图象，该函数的最小值是 ．
【答案】﹣4
【解答】解：由函数图象可得：﹣＝﹣＝﹣1，
解得：b＝2，
∵图象经过（﹣3，0）点，
∴0＝（﹣3）2﹣3×2+c，
解得：c＝﹣3，
故二次函数解析式为：y＝x2+2x﹣3，
则二次函数的最小值为：＝＝﹣4．
故答案为：﹣4．
10．（2022•株洲）已知二次函数y＝ax2+bx﹣c（a≠0），其中b＞0、c＞0，则该函数的图象可能为（ ）
A．B．
C．D．
【答案】C
【解答】解：∵c＞0，
∴﹣c＜0，
故A，D选项不符合题意；
当a＞0时，
∵b＞0，
∴对称轴x＝＜0，
故B选项不符合题意；
当a＜0时，b＞0，
∴对称轴x＝＞0，
故C选项符合题意，
故选：C．
11．（2022•泰安）抛物线y＝ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：
下列结论不正确的是（ ）
A．抛物线的开口向下
B．抛物线的对称轴为直线x＝
C．抛物线与x轴的一个交点坐标为（2，0）
D．函数y＝ax2+bx+c的最大值为
【答案】C
【解答】解：由表格可得，
，
解得，
∴y＝﹣x2+x+6＝﹣（x﹣）2+＝（﹣x+3）（x+2），
∴该抛物线的开口向下，故选项A正确，不符合题意；
该抛物线的对称轴是直线x＝，故选项B正确，不符合题意，
∵当x＝﹣2时，y＝0，
∴当x＝×2﹣（﹣2）＝3时，y＝0，故选项C错误，符合题意；
函数y＝ax2+bx+c的最大值为，故选项D正确，不符合题意；
故选：C．
12．（2022•牡丹江）如图，抛物线y＝ax2+bx+c（a≠0）的对称轴是直线x＝﹣2，并与x轴交于A，B两点，若OA＝5OB，则下列结论中：①abc＞0；②（a+c）2﹣b2＝0；③9a+4c＜0；④若m为任意实数，则am2+bm+2b≥4a，正确的个数是（ ）
A．1B．2C．3D．4
【答案】C
【解答】解：①观察图象可知：a＞0，b＞0，c＜0，
∴abc＜0，故①错误；
②∵对称轴为直线x＝﹣2，OA＝5OB，
可得OA＝5，OB＝1，
∴点A（﹣5，0），点B（1，0），
∴当x＝1时，y＝0，即a+b+c＝0，
∴（a+c）2﹣b2＝（a+b+c）（a+c﹣b）＝0，故②正确；
③抛物线的对称轴为直线x＝﹣2，即﹣＝﹣2，
∴b＝4a，
∵a+b+c＝0，
∴5a+c＝0，
∴c＝﹣5a，
∴9a+4c＝﹣11a，
∵a＞0，
∴9a+4c＜0，故③正确；
④当x＝﹣2时，函数有最小值y＝4a﹣2b+c，
由am2+bm+c≥4a﹣2b+c，可得am2+bm+2b≥4a，
∴若m为任意实数，则am2+bm+2b≥4a，故④正确；
故选：C．x
﹣2
﹣1
0
1
y
0
4
6
6