2024-2025学年山东省泰安市新泰市高三上册10月月考数学检测试卷

这是一份2024-2025学年山东省泰安市新泰市高三上册10月月考数学检测试卷，共4页。试卷主要包含了选择题，多项选择题，填空题，双空题，解答题等内容，欢迎下载使用。
一、选择题（共40分）
1. 向量，若，则的值为（ ）
A. B.
C. D.
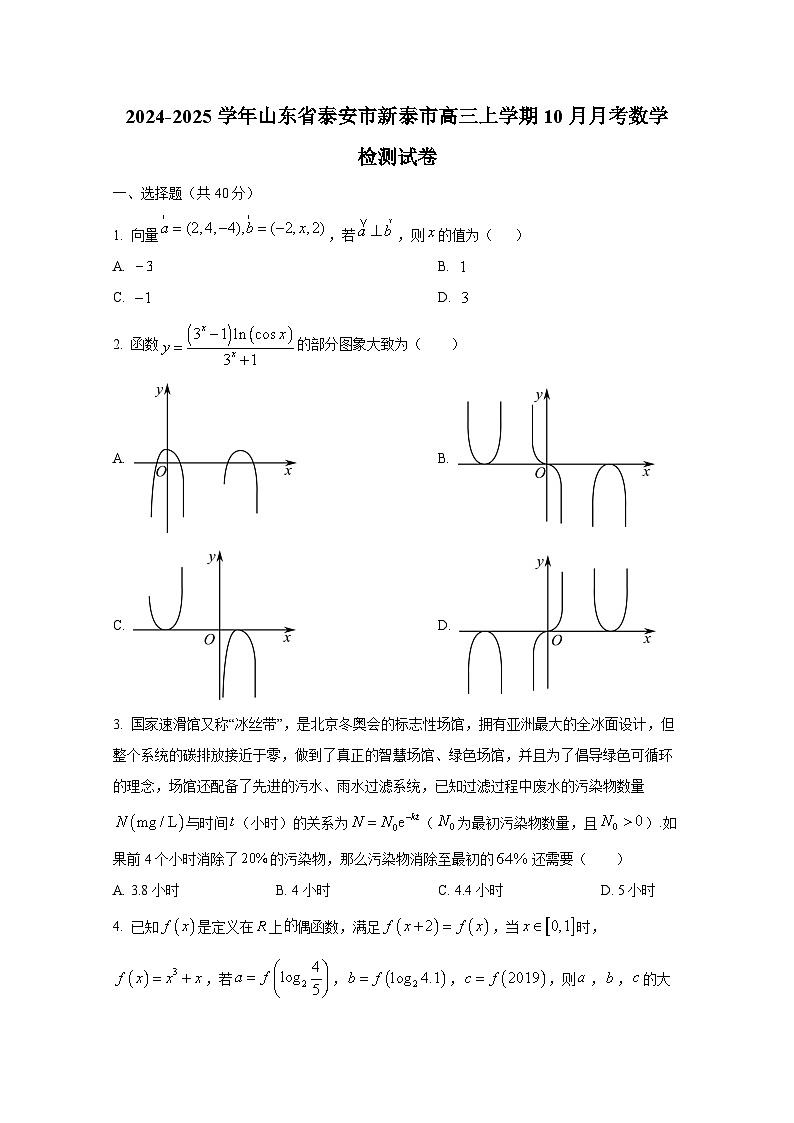
2. 函数的部分图象大致为（ ）
A. B.
C. D.
3. 国家速滑馆又称“冰丝带”，是北京冬奥会的标志性场馆，拥有亚洲最大的全冰面设计，但整个系统的碳排放接近于零，做到了真正的智慧场馆、绿色场馆，并且为了倡导绿色可循环的理念，场馆还配备了先进的污水、雨水过滤系统，已知过滤过程中废水的污染物数量与时间（小时）的关系为（为最初污染物数量，且）.如果前4个小时消除了的污染物，那么污染物消除至最初的还需要（ ）
A. 3.8小时B. 4小时C. 4.4小时D. 5小时
4. 已知是定义在上偶函数，满足，当时，，若，，，则，，的大小关系为（ ）
A. B. C. D.
5. 已知，则（ ）
A. 25B. 5C. D.
6. 设函数，若，则的最小值为（ ）
A B. C. D. 1
7. 若a，，，则的最大值为（ ）
A. B. C. 2D. 4
8. 已知0为函数极小值点，则a的取值范围是（ ）
A. B.
C D.
二、多项选择题（共18分）
9. 若，则下列不等式成立的是（ ）
A. B.
C. D.
10. 已知函数，，则（ ）
A. 与的值域相同
B. 与的最小正周期相同
C. 曲线与有相同的对称轴
D. 曲线与有相同的对称中心
11. 已知，且，则（ ）
A. ab的最大值为B. 的最小值为
C. 的最小值为D. 的最大值为3
三、填空题（共10分）
12. 函数的最小正周期为________．
13. 若是偶函数，则实数的值为__________.
四、双空题（共5分）
14 已知，则________；______．
五、解答题（共77分）
15. 2022年新冠肺炎仍在世界好多国家肆虐，并且出现了传染性更强的“德尔塔”变异毒株、“拉姆达”变异毒株，尽管我国疫情得到了很好的遏制，但由于整个国际环境的影响，时而也会出现一些散发病例，故而抗疫形势依然严峻，日常防护依然不能有丝毫放松．在日常防护中，医用防护用品必不可少，某公司一年购买某种医用防护用品600吨，每次都购买x吨，运费为6万元/次，一年的存储费用为万元.一年的总费用y（万元）包含运费与存储费用.
（1）要使总费用不超过公司年预算260万元，求x的取值范围.
（2）要使总费用最小，求x的值.
16. 设函数
（1）若不等式对一切实数x恒成立，求a的取值范围；
（2）解关于的不等式：．
17. 如图，已知四棱锥的底面是平行四边形，，，是边长为2的等边三角形，，是线段的中点.
（1）求证：平面平面；
（2）若，是否存在，使得平面和平面夹角的余弦值为？若存在，求出的值；若不存在，请说明理由.
18. 如图所示为直四棱柱，，分别是线段的中点.
（1）证明:平面；
（2）求直线BC与平面所成角的正弦值，并判断线段BC上是否存在点，使得平面，若存在，求出BP的值，若不存在，请说明理由.
19. 如图，四边形ABCD是边长为2的菱形，，将沿BD折起到的位置，使．

（1）求证：平面平面ABD；
（2）求直线与平面所成角的正弦值．