山东省泰安市新泰市弘文中学2024-2025学年高二上学期期中学情检测数学试题

这是一份山东省泰安市新泰市弘文中学2024-2025学年高二上学期期中学情检测数学试题，共8页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．已知空间向量,,满足,,,,则与的夹角为( )
A.B.C.D.
2．若圆与圆相切，则实数a的值为( )
A.B.C.或D.3r或r
3．已知圆，点，，在圆M上存在点P，使得，则实数a的取值范围为( )
A.B.C.D.
4．已知两圆和相交，则实数a的取值范围为( )
A.B.C.D.
5．已知圆，圆，则圆，的位置关系为( )
A.内含B.外切C.相交D.外离
6．已知P是圆上一点，Q是圆上一点，则的最小值为( )
A.1B.C.2D.
7．以点为圆心，且与圆相外切的圆的方程为( )
A.B.
C.D.
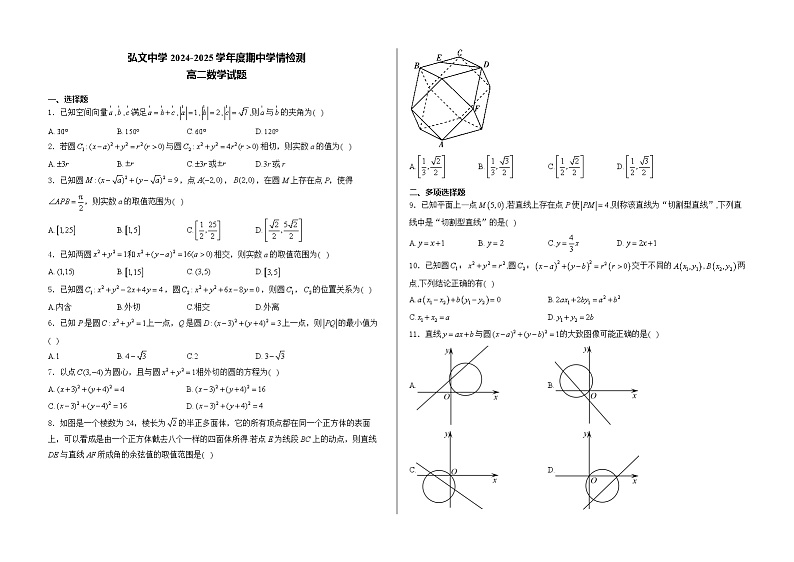
8．如图是一个棱数为24，棱长为的半正多面体，它的所有顶点都在同一个正方体的表面上，可以看成是由一个正方体截去八个一样的四面体所得.若点E为线段BC上的动点，则直线DE与直线AF所成角的余弦值的取值范围是( )
A.B.C.D.
二、多项选择题
9．已知平面上—点,若直线上存在点P使,则称该直线为“切割型直线”,下列直线中是“切割型直线”的是( )
A. B.C.D.
10．已知圆：,圆：交于不同的,两点,下列结论正确的有( )
A. B.
C.D.
11．直线与圆的大致图像可能正确的是( )
A.B.
C.D.
三、填空题
12．在平面直角坐标系中，,是直线l上不同的两点，直线l上的向量以及与它平行的非零向量都称为直线l的方向向量.已知直线l的一个方向向量坐标为，则直线l的倾斜角为______.
13．已知是方程组的解，
则方程组的解是______．
14．平面直角坐标系中，矩形的四个顶点为，，，，，光线从边上一点沿与x轴成角的方向发射到边上的点，被反射到上的点，再被反射到上的点，最后被反射到x轴上的点，若，则的取值范围是________.
四、解答题
15．已知圆.
(1)若直线l过定点且与圆C相切,求直线l的方程;
(2)若直线与圆C交于A,B两点,求的最小值.
16．如图，在四棱柱中，二面角，均为直二面角.
（1）求证：平面；
（2）若，，二面角的正弦值为，求的值.
17．如图,长方体中,点E,F分别在,上,且,.
（1）求证:平面AEF;
（2）当,时,求平面AEF与平面的夹角的余弦值.
18．如图,在四棱锥中,底面为矩形,M在棱上且,,,平面,在棱上存在一点Q满足平面.
(1)证明：平面平面;
(2)求平面与平面夹角的余弦值.
19．如图,已知AB是圆柱下底面圆的直径,点C是下底面圆周上异于A,B的动点,CD,BE是圆柱的两条母线.
（1）求证:平面BCDE;
（2）若,,圆柱的母线长为,求平面ADE与平面ABC所成的锐二面角的余弦值.
参考答案
1．答案：D
解析：设与的夹角为,由,得,两边同时平方得,所以1,解得,又,所以.
2．答案：C
解析：圆的圆心为，半径为r，圆的圆心为，半径为2r.
①当两圆外切时，有，此时.
②当两圆内切时，有，此时.
综上，当时，两圆外切；当时，两圆内切.故选C.
3．答案：C
解析：如图，构造圆，当圆O与圆M有公共点P时，，即圆O与圆M的关系可以为相切或相交，所以解得.故选C.
4．答案：C
解析：由圆，知圆心为，半径，由圆，知圆心为，半径，
所以根据两圆相交得，，则.故选C.
5．答案：C
解析：圆，化为，圆心为，半径为；圆，化为，圆心为，半径为.两圆心距离为，因为，所以圆与圆相交.故选C.
6．答案：B
解析：因为，，所以，且两圆的半径分别为，，，即两圆外离，所以的最小值为.故选B.
7．答案：B
解析：由题意可知，两圆的圆心距为，设圆C的半径为r，因为两圆相外切，所以，得，所以圆C的方程为.故选B.
8．答案：C
解析：由题意得该几何体有6个面是边长为的正方形，8个面是边长为的等边三角形.
在原正方体中建立如图所示的空间直角坐标系，易知原正方体的棱长为2，则，，，设，，，.设直线DE与直线AF所成的角为，则直线DE与直线AF所成角的余弦值，而，故，则.故选C.
9．答案：BC
解析：所给直线上的点到定点M距离能否取4,可通过求各直线上的点到点M的最小距离,即点M到直线的距离来分析.
A.因为,故直线上不存在点到M距离等于4,不是“切割型直线”;
B.因为,所以在直线上可以找到两个不同的点,使之到点M距离等于4,是“切割型直线”;
C.因为,直线上存在一点,使之到点M距离等于4,是“切割型直线”;
D.因为,故直线上不存在点到M距离等于4,不是“切割型直线”.
10．答案：ABC
解析：由题意,由圆的方程可化为
两圆的方程相减可得直线AB的方程为：,即,
分别把,两点代入可得：,
两式相减可得,即,所以选项A、B正确;
由圆的性质可得,线段AB与线段互相平分,所以,.
所以选项C正确,选项D不正确.
11．答案：AC
解析：A：直线不经过第四象限，所以，，所以圆的圆心在第一象限，因此本选项可能正确；
B：直线不经过第一象限，所以，，所以圆的圆心在第三象限，因此本选项不可能正确；
C：直线不经过第一象限，所以，，所以圆的圆心在第三象限，又因为该圆经过原点，所以有，在圆的方程中，令，
得或，因为，
所以，因此本选项可能正确；
D：直线不经过第二象限，所以，，所以圆的圆心在第四象限，又因为该圆经过原点，所以有，在圆的方程中，令，
得或，因为，
所以，因此本选项不可能正确，
故选：AC.
12．答案：
解析：直线l的一个方向向量为
,
,
直线l倾斜角为.
13．答案：
解析：由题意，代入方程组可得，
所以当时，代入方程组，
可得，成立，
所以方程组的解是，
故答案为：
14．答案：
解析：点沿与x轴成角的方向发射到边上的点，
则，
有，则，，
，，
，，
即，
，解得.
故答案为：
15．答案：(1)直线l的方程为和.
(2)
解析：(1)已知圆心,半径,
当直线斜率存在时,设直,即,
圆心到直线l的距离为,解方程可得,
此时直线方程为,整理得.
当直线斜率不存在时,直线l的方程为,满足题意.
所以直线l的方程为和.
(2)直线l的方程可化为点斜式,所以l过定点.
又点在圆C内,当直线l与直线垂直时,直线l被圆截得的弦最小.
因为,所以l的斜率,
所以l的方程为,即,
因为,,
此时
所以当时,的最小值为.
16．答案：（1）证明见解析
（2）
解析：（1）证明：在平面内取点E，过E作直线，由于二面角为直二面角，
即平面平面，平面平面，
平面，故平面，平面，故；
同理过E作直线，由于二面角为直二面角，
即平面平面，平面平面，
平面，故平面，平面，故；
由于，不平行，故a，b不重合，，平面，
故平面；
（2）由题意可得，可以A为坐标原点，以，，所在直线为x，y，z轴，建立空间直角坐标系，
设，，，，，，
则，，，，
设平面的法向量为，则，
即，令，则，
设平面的法向量为，则，
即，令，则，
二面角的正弦值为，故其余弦值的绝对值为，
即，即，解得，
故.
17．答案：（1）证明见解析
（2）
解析：（1）因为平面,平面,所以,
又且,,平面,所以平面,
且平面,故,同理,,
AE,平面AEF,,
所以平面AEF.
（2）以A为原点,AB,AD,所在直线为x,y,z轴建立空间直角坐标系,如图:
则,,,,
在平面中,,
设平面的一个法向量为,
则,可取
由（1）知,平面AEF的一个法向量为
设平面AEF与平面的夹角为,
则
故所求的夹角的余弦值为.
18．答案：(1)证明见解析;
(2).
解析：(1)在四棱锥中,底面为矩形,则,
由平面,平面,得,
而,,平面,则平面,又平面,
所以平面平面.
(2)依题意,直线,,两两垂直,
以点D为原点,直线,,分别为x,y,z轴建立空间直角坐标系,
则,,,,由,得,令,,
则有,即,,
,,由平面,得存在实数p,q使,
即,解得,,
,,,
设平面的法向量,则,令,,
设平面的法向量,则,令,,
所以平面与平面夹角的余弦值为.
19．答案：（1）证明见解析;
（2）
解析：（1）因为AB是底面的一条直径,C是下底面圆周上异于A,B的动点,
所以,
又因为CD是圆柱的一条母线,所以底面ACB,
而底面ACB,所以,
因为平面BCDE,平面BCDE,且,
所以平面BCDE,
又因为,所以平面平面BCDE;
（2）如图所示,
过作圆柱的母线AM,连接DM,EM
因为底面//上底面DME,所以即求平面ADE与平面DME所成锐二面角的大小,
因为M,E在底面的射影为A,B,且AB为下底面的直径,所以EM为上底面的直径,
因为AM是圆柱的母线,所以平面DME,
又因为EM为上底面的直径,所以,而平面,
所以为平面ADE与平面DME所成的二面角的平面角,
又因为D在底面射影为C,所以,,
所以,又因为母线长为,所以,
又因为平面DME,平面DME,所以,
所以,
所以,
即平面ADE与平面ABC所成的锐二面角的余弦值为.