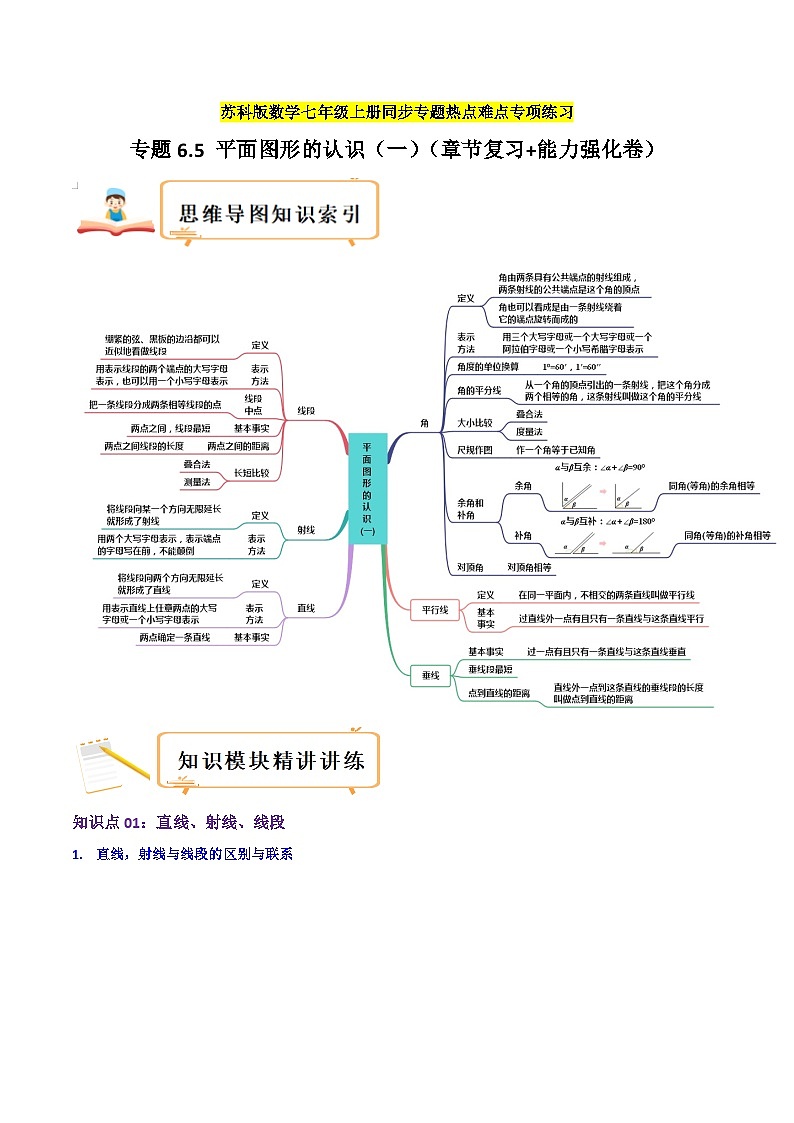
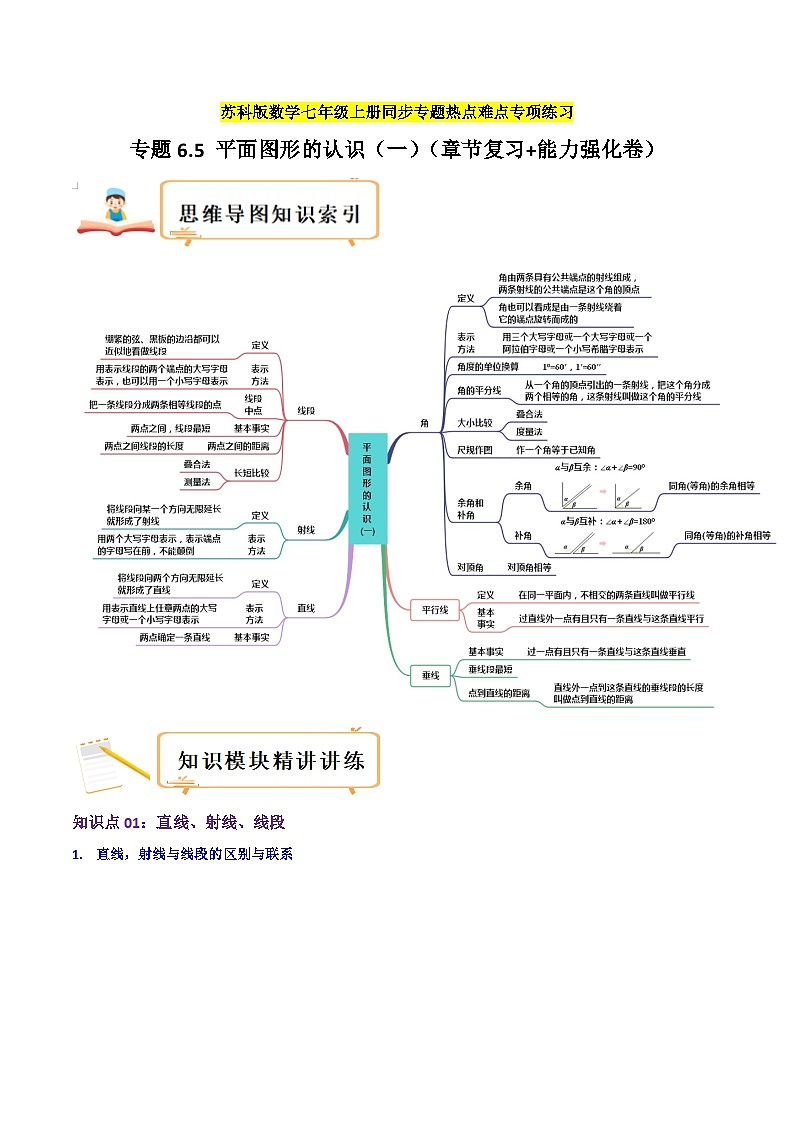
苏科版数学七年级上册期末复习专题6.5 平面图形的认识（一）（章节复习+能力强化卷）（2份，原卷版+教师版）

这是一份苏科版数学七年级上册期末复习专题6.5 平面图形的认识（一）（章节复习+能力强化卷）（2份，原卷版+教师版），文件包含苏科版数学七年级上册期末复习专题65平面图形的认识一章节复习+能力强化卷教师版doc、苏科版数学七年级上册期末复习专题65平面图形的认识一章节复习+能力强化卷学生版doc等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。

知识点01：直线、射线、线段
直线，射线与线段的区别与联系
2. 基本性质
(1)直线的性质: ． (2)线段的性质: ．
知识要点：①本知识点可用来解释很多生活中的现象. 如：要在墙上固定一个木条，只要两个钉子就可以了，因为如果把木条看作一条直线，那么两点可确定一条直线.
②连接两点间的线段的长度，叫做两点的距离.
3.画一条线段等于已知线段
（1）度量法：可用直尺先量出 ,再 .
（2）用尺规作图法：用圆规在射线AC上截取AB＝ａ，如下图：
4．线段的比较与运算
（1）线段的比较：比较两条线段的长短，常用两种方法，一种是 ；一种是 .
（2）线段的和与差：如下图，有AB+BC＝AC，或AC＝a+b；AD＝AB-BD.
（3）线段的中点：把一条线段分成两条相等线段的点，叫做线段的中点．如下图，有：.
知识要点：①线段中点的等价表述：如上图，点M在线段上，且有，则点M为线段AB的中点.
②除线段的中点（即二等分点）外，类似的还有线段的三等分点、四等分点等.
如下图，点M,N,P均为线段AB的四等分点，则有.
（4）线段的延长线：如下图，图①称为延长线段AB，或称为反向延长线段BA；图②称为延长线段BA，或称为反向延长线段AB. 叫做原线段的延长线.
知识点02：角
1．角的概念及其表示
（1）角的定义： 叫做角，这个点叫做角的顶点， 是角的边；此外，角也可以看作 .
(2)角的表示方法：角通常有三种表示方法：一是用 表示，二是 的一个大写英文字母表示，三是用 表示.例如下图：
知识要点：①角的两种定义是从不同角度对角进行的定义.
②当一个角的顶点有多个角的时候，不能用顶点的一个大写字母来表示.
2.角的分类
3.角的度量
1周角＝360°，1平角＝180°，1°＝60′，1′＝60″.
知识要点：①度、分、秒的换算是60进制，与时间中的小时分钟秒的换算相同.
②度分秒之间的转化方法：由度化为度分秒的形式(即从高级单位向低级单位转化)时用乘法逐级进行；由度分秒的形式化成度(即低级单位向高级单位转化)时用除法逐级进行.
③同种形式相加减：度加（减）度，分加（减）分，秒加（减）秒；超60进一，减一
成60.
4.角的平分线
从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线，例如：如下图，因为OC是∠AOB的平分线，所以∠1＝∠2＝∠AOB，或∠AOB＝2∠1＝2∠2.
类似地，还有角的三等分线等.
5．余角、补角、对顶角
（1）余角、补角：
若∠1+∠2＝90°， 则∠1与∠2互为余角.其中∠1是∠2的余角，∠2是∠1的余角.
若∠1+∠2＝180°，则∠1与∠2互为补角.其中∠1是∠2的补角，∠2是∠1的补角.
结论: 同角(或等角)的余角相等；同角(或等角)的补角相等.
知识要点：①余角(或补角)是两个角的关系，是 出现的，单独一个角不能称其为 ②一个角的余角(或补角)可以 ，但是它们的 是相同的.
③只考虑 ，与 无关．
④“等角是相等的几个角”，而“同角是同一个角”．
（2）对顶角： ．
知识点03：平行与垂直
1. 同一平面内的两条直线的位置关系:平行与相交. 平行用符号“∥”表示.
知识要点： 叫做相交直线，这个公共点叫做交点.
2.垂线
（1）垂线的定义：两条直线相交所成的四个角中，有一个角是直角时，就称这两条直线 ，其中一条直线叫做 ，它们的交点叫 ．垂直用符号“⊥”表示，如下图．
（2）垂线的性质：
①在同一平面内， 与已知直线垂直．
② ．
（3）点到直线的距离： ，叫做点到直线的距离．
一、选择题（每题2分，共20分）
1．（本题2分）（2023春·江苏南通·七年级统考期中）如图，直线相交于点平分．若，则的度数为( )

A．B．C．D．
2．（本题2分）（2023秋·江苏无锡·七年级统考期末）如图，直线、相交于点O，，图中与互补的角有（ ）
A．1个B．2个C．3个D．4个
3．（本题2分）（2023春·江苏无锡·七年级校联考期末）如图，C、D在线段BE上，下列说法：①直线上以B、C、D、E为端点的线段共有6条；②若，，则以A为顶点的所有小于平角的角的度数和为；③若，，点F是线段上任意一点，则点F到点B、C、D、E的距离之和最小值为14，其中说法正确的个数有（ ）；
A．0个B．1个C．2个D．3个
4．（本题2分）（2022春·江苏南通·七年级校考阶段练习）如果两个角的两边分别垂直，而其中一个角的比另一个角少，那么这两个角的度数是（ ）
A．和B．、或、C．都是D．、或、
5．（本题2分）（2022秋·江苏·七年级专题练习）如图，将两个三角尺的直角与顶点O重合在一起，若，OE为的平分线，则的度数为（ ）
A．36B．45C．60D．72
6．（本题2分）（2022秋·七年级单元测试）一副三角板ABC、DBE，如图1放置，（∠D＝30°、∠BAC＝45°），将三角板DBE绕点B逆时针旋转一定角度，如图2所示，且0°＜∠CBE＜90°，则下列结论中正确的是（ ）
①∠DBC+∠ABE的角度恒为105°；
②在旋转过程中，若BM平分∠DBA，BN平分∠EBC，∠MBN的角度恒为定值；
③在旋转过程中，两块三角板的边所在直线夹角成90°的次数为2次；
④在图1的情况下，作∠DBF＝∠EBF，则AB平分∠DBF．
A．①B．②C．①②④D．①②③④
7．（本题2分）（2022秋·七年级单元测试）图，C是直线AB上一点，CD⊥AB，EC⊥CF，则图中互余的角的对数与互补的角的对数分别是（ ）
A．3，4B．4，7C．4，4D．4，5
8．（本题2分）（2020秋·江苏无锡·七年级校考阶段练习）如图，点M在线段AN的延长线上，且线段MN=20，第一次操作：分别取线段AM和AN的中点；第二次操作：分别取线段和的中点；第三次操作：分别取线段和的中点；……连续这样操作10次，则每次的两个中点所形成的所有线段之和( )
A．B．C．D．
9．（本题2分）（2021秋·江苏·七年级专题练习）观察下列图形，并阅读图形下面的相关文字，如图所示∶两条直线相交，三条直线相交，四条直线相交，最多有一个交点，最多有三个交点；最多有6个交点，像这样，10条直线相交，最多交点的个数是( )
A．40个B．45个C．50个D．55个
10．（本题2分）（2021秋·江苏无锡·七年级校考期中）如图，在公路MN两侧分别有，七个工厂，各工厂与公路MN（图中粗线）之间有小公路连接．现在需要在公路MN上设置一个车站，选择站址的标准是“使各工厂到车站的距离之和越小越好”．则下面结论中正确的是（ ）
①车站的位置设在C点好于B点；
②车站的位置设在B点与C点之间公路上任何一点效果一样；
③车站位置的设置与各段小公路的长度无关；
④车站的位置设在BC段公路的最中间处要好于设在点B及点C处．
A．①③B．③④C．②③D．②
二、填空题（每题2分，共20分）
11．（本题2分）（2023秋·江苏宿迁·七年级统考期末）如图，直线、相交于点，，．则的度数为 ．

12．（本题2分）（2022秋·江苏淮安·七年级统考期末）线段，是的中点，是的中点，是的中点，是的中点，依此类推……，线段的长为 ．
13．（本题2分）（2023秋·江苏南京·七年级南京玄武外国语学校校考期末）一副三角板如图摆放，若，则 °．
14．（本题2分）（2023秋·江苏扬州·七年级统考期末）如图，已知线段，点O是线段中点，若点C在线段上，，点P是线段的中点，则线段的长为 ．
15．（本题2分）（2023春·江苏扬州·七年级期中）如图，已知，在内部且，下列说法：①如果，则图中有两对互余的角；②如果作平分，则；③如果作平分，在内部，且，则平分；④如果在外部分别作的余角，则；其中正确的有 ．
16．（本题2分）（2022秋·江苏南通·七年级校联考期末）如图，，点C是线段延长线上一点，在线段上取一点N，使，点M为线段的中点，则 ．
17．（本题2分）（2022秋·江苏·七年级期末）如图，有公共端点的两条线段，组成一条折线，若该折线上一点把这条折线分成相等的两部分，我们把这个点叫做这条折线的“折中点”．已知点是折线的“折中点”，点为线段的中点，，，则线段的长为 ．
18．（本题2分）（2022秋·江苏·七年级专题练习）如图，于点O，为内的一条射线，点D在的延长线上，平分，在图中的所有角中，当与互补的角有且只有两个时，则的度数为 ．
19．（本题2分）（2023秋·江苏泰州·七年级统考期末）如图，于点，，射线从出发，绕点以每秒的速度顺时针向终边旋转，同时，射线从出发，绕点以每秒的速度顺时针向终边旋转，当、中有一条射线到达终边时，另一条射线也随之停止．在旋转过程中，设，，则与之间的数量关系为 ．
20．（本题2分）（2022秋·江苏盐城·七年级校考阶段练习）如图，在数轴上剪下6个单位长度（从到5）的一条线段，并把这条线段沿某点向左折叠，然后在重叠部分的某处剪一刀得到三条线段，发现这三条线段的长度之比为，则折痕处对应的点表示的数可能是 ．
三、解答题（共60分）
21．（本题6分）（2023春·江苏南京·七年级统考期中）请结合题意，在横线上填上合适的推理依据．
如图，，，求证：．

证明：∵(已知)
∴(垂直的定义)
∵(已知)
∴____________(____________________)
∴______(____________________)
又∵(已知)
∴(____________________)
∴(____________________)
∴(两直线平行，同位角相等)
∴．
22．（本题6分）（2022秋·江苏·七年级专题练习）如图，直线相交于点O，，平分．
(1)若，求的度数；
(2)若，求的度数．
23．（本题8分）（2022秋·江苏·七年级专题练习）如图，P是线段上一点，，C，D两动点分别从点P，B同时出发沿射线向左运动，到达点A处即停止运动．
(1)若点C，D的速度分别是，．
①当动点C，D运动了2s，且点D仍在线段上时，_________cm；
②若点C到达中点时，点D也刚好到达的中点，则_________；
(2)若动点C，D的速度分别是，，点C，D在运动时，总有，求的长
24．（本题8分）（2023春·江苏苏州·七年级统考期末）如图，在中，，，垂足为，平分．

(1)已知，，求的度数；
(2)已知，求证：．
25．（本题8分）（2022秋·江苏淮安·七年级淮阴中学新城校区校考期末）【阅读材料】：
如图1，将线段放在直线上，然后将线段绕点O按如下方式旋转：第1步，从（在上）开始先顺时针旋转锐角至；第2步，从开始继续同向旋转至；第3步，从开始继续旋转至，…．当转到位置时弹回，逆时针向位置旋转；当转到位置时再弹回，继续向位置旋转，…如此反复．

例如：当时， 的位置如图2所示，其中第4步旋转到后弹回，即．
【解决问题】：
(1)当时，的位置如图3所示．
① ， ；
②求出的度数．
(2)当时, 且，则的值为 ；
(3)若在整个旋转过程中， 是第一次经过弹回后而得到的位置，则的范围是 ；（请用“＞”，“＜”，“≥”，“≤”进行表示）
26．（本题8分）（2023秋·江苏盐城·七年级统考期末）如图1，点A、O、B依次在直线上，现将射线绕点O沿顺时针方向以每秒的速度旋转，同时射线绕点O沿逆时针方向以每秒的速度旋转，直线保持不动，如图2，设旋转时间为（的值在0到之间，单位：秒）．
(1)当时，求的度数；
(2)在运动过程中，当首次达到时，求的值；
(3)在旋转过程中是否存在这样的，使得射线垂直射线？如果存在，请求出的值；如果不存在，请说明理由．
27．（本题8分）（2023春·江苏苏州·七年级苏州草桥中学校考期中）一副三角板（中，，，中，，，）按如图①方式放置，如图②将绕点A按逆时针方向，以每秒5°的速度旋转，设旋转的时间为秒．
(1)图①中，______°；
(2)在绕点A旋转的过程中，当与的一边平行时，求的值；
(3)在绕点A旋转的过程中，探究与之间的数量关系．
28．（本题8分）（2023春·江苏宿迁·七年级统考期中）我们将内角互为对顶角的两个三角形称为“对顶三角形”．例如，在图1中，的内角与的内角互为对顶角，则与为对顶三角形，根据三角形内角和定理知“对顶三角形”有如下性质：．
(1)【性质理解】
如图2，在“对顶三角形”与中，，，，则；
(2)【性质应用】
如图3，和的平分线交于点E，则与、之间存在何种数量关系．请说明理由；
(3)【拓展提高】
如图4，、是的角平分线，且和的平分线和相交于点P，设，直接写出的度数（用含的式子表示）﹒
∠β
锐角
直角
钝角
平角
周角
范围
0＜∠β＜90°
∠β＝90°
90°