初中数学3.4 一元一次方程的应用教学演示课件ppt

这是一份初中数学3.4 一元一次方程的应用教学演示课件ppt，文件包含34第5课时方案问题pptx、34第5课时分段计费方案问题docx等2份课件配套教学资源，其中PPT共20页， 欢迎下载使用。
1. 会列一元一次方程解有关分段计费、方案设计等问题，在具体情境中建立方程模型.2. 体验建立方程模型解决问题的一般过程；体会模型转化和方程思想，增强应用意识和应用能力.3. 体会分类讨论思想和方程思想，感受数学与生活的联系，激发学生学习数学的热情.重点：在实际背景中找到等量关系，建立分段计费问 题和方案设计的方程模型，并解决实际问题.难点：理解题意，将实际问题转化为数学问题.
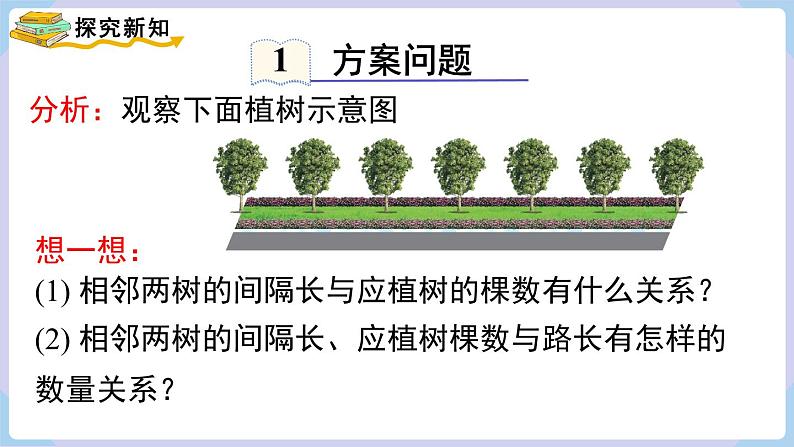
探究 现有树苗若干棵，计划栽在一段公路的一侧，公路的两端各栽 1 棵，并且相邻两棵树的间隔相等.
方案一：如果每隔 5 m 栽 1 棵，则树苗缺 21 棵；
方案二：如果每隔 5.5 m 栽 1 棵，则树苗正好用完.
根据以上方案，请算出原有树苗的棵数和这段路的长度.
(1) 相邻两树的间隔长与应植树的棵数有什么关系？(2) 相邻两树的间隔长、应植树棵数与路长有怎样的数量关系？
分析：观察下面植树示意图
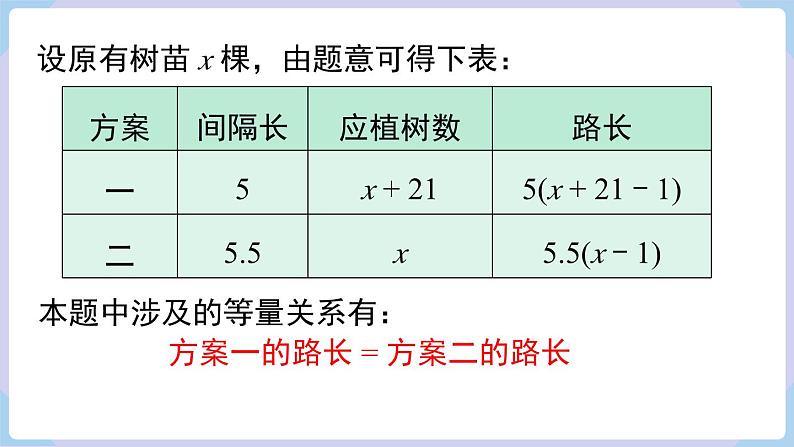
设原有树苗 x 棵，由题意可得下表：
本题中涉及的等量关系有：
方案一的路长 = 方案二的路长
解：设原有树苗 x 棵，根据等量关系， 得 5(x + 21 - 1) = 5.5(x - 1) ， 解得 x = 211. 因此，这段路长为 5×(211 + 20) = 1155 (m). 答：原有树苗 211 棵，这段路的长度为 1155 m．
间隔问题应用比较普遍，如路边种树，街道装路灯等． 需要注意：(1)两个端点都种上树(装上灯)，则树数－1＝间隔数；(2)两个端点都不种树(装上灯)，则树数＋1＝间隔数．
1. 某道路一侧原有路灯 106 盏 (两端都有)，相邻两盏灯的距离为 36 m，现计划全部更换为新型的节能灯，且相邻两盏灯的距离变为 70 m，则需安装新型节能灯多少盏？
答：需安装新型节能灯 55 盏.
探究2 购买空调时，需要综合考虑空调的价格和耗电情况. 某人打算从两款空调中选购一台，下表是这两款空调的部分基本信息. 如果电价是 0.5 元/(kw.h). 请你分析他购买、使用哪款空调综合费用较低.
电费 0.5×640×使用年数 元
电费 0.5×800×使用年数 元
综合费用 = 空调的售价 + 电费
设空调的使用年数是 t，
则 1 级效能空调的综合费用 (单位：元) 是 3000 + 0.5×640t，
即 3000 + 320t
3 级效能空调的综合费用 (单位：元) 是 2600 + 0.5×800t，
即 2600 + 400t
问题1： t 取什么值时，两款空调的综合费用相等？
3000 + 320t = 2600 + 400t
问题2：如何比较两款空调的综合费用？
比较 3000 + 320t 与 2600 + 400t 的大小.
方法一：运用整式的加减
(3000 + 320t) - (2600 + 400t)
= 3000 + 320t - 2600 - 400t
= 400 - 80t
= 80(5 - t)
当 t < 5 时，80(5 - t) > 0，
3000 + 320t > 2600 + 400t；
当 t > 5 时，80(5 - t) < 0，
3000 + 320t < 2600 + 400t.
(大数-小数＞0，小数-大数＜0)
方法二：把表示 3 级能效空调的综合资用的式子 2600 + 400t 变形为 1 级能效空调的综合费用与另外一个式于的和.
2600 + 400t = (3000 + 320t) + (80t - 400)
= (3000 + 320t) + 80(t - 5)
当 t < 5 时，80(5 - t) 是负数，
这表明 3 级能效空调的综合费用较低；
当 t > 5 时，80(5 - t) 是正数，
这表明 1 级能效空调的综合费用较低.
问题3：你认为哪种空调更划算呢？
同样是 1.5 匹的空调，1 级能效空调虽然售价高，但由于比较省电，使用年份长 (超过 5 年) 时综合费用反而低. 根据相关行业标准，空调的安全使用年限是 10 年 (从生产日期计起)，因此购买、使用 1 级能效空调更划算.
当 t = 5 时，两款空调的综合费用相等；
当 t < 5 时，3 级能效空调的综合费用较低；
当 t > 5 时，1 级能效空调的综合费用较低.
2. 小翼打算办一张电话卡，有如下计费方式：
设小翼主叫时间为 t，当 t≤150 时，选 划算；
当 时，两种方案计费相等；
当 时，选择方案二划算.
58 + 0.25(t - 150)
= 0.25t + 20.5
88 + 0.19(t - 350)
= 0.19t + 21.5
0.25t + 20.5 = 0.19t + 21.5
① 要善于分析问题中的不变量，并利用不变量来列方程；② 要善于用不同的方式表示同一个量，由此得到相等关系，从而列出方程．
1. 某校组织师生去参观三峡工程建设，若单独租用30 座客车若干辆，则刚好坐满；若单独租用 40 座客车，则可少租一辆，且余 20 个座位，求该校参观三峡工程建设的人数．
解：设需要 30 座的车是 x 辆，根据题意，得 30x＝40(x－1)－20，解得 x＝6.参观人数＝30×6＝180 (人)．答：该校参观三峡工程建设的人数为 180 人．
4. 某市生活拨号上网有两种收费方式，用户可以任选 其一. A 计时制：0.05 元/分钟；B 包月制：60 元/月 (限一部个人住宅电话上网). 此外，两种上网 方式都得加收通信费 0.02 元/分钟． (1) 某用户某月上网时间为 x 小时，请分别写出两种 收费方式下该用户应该支付的费用；
解：采用计时制：(0.05＋0.02)×60x＝4.2x， 采用包月制：60＋0.02×60x＝60＋1.2x.