2024-2025学年重庆市开州开区高三上册第三次月考数学检测试题（含解析）

这是一份2024-2025学年重庆市开州开区高三上册第三次月考数学检测试题（含解析），共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．已知集合，则（ ）
A．B．C．D．
2．若，则（ ）
A．B．C．D．
3．已知向量，．若，则（ ）
A．1B．C．12D．
4．已知，，则的值为（ ）
A．B．C．D．
5．已知圆锥PO的底面半径为，轴截面的面积为，则该圆锥的体积为（ ）
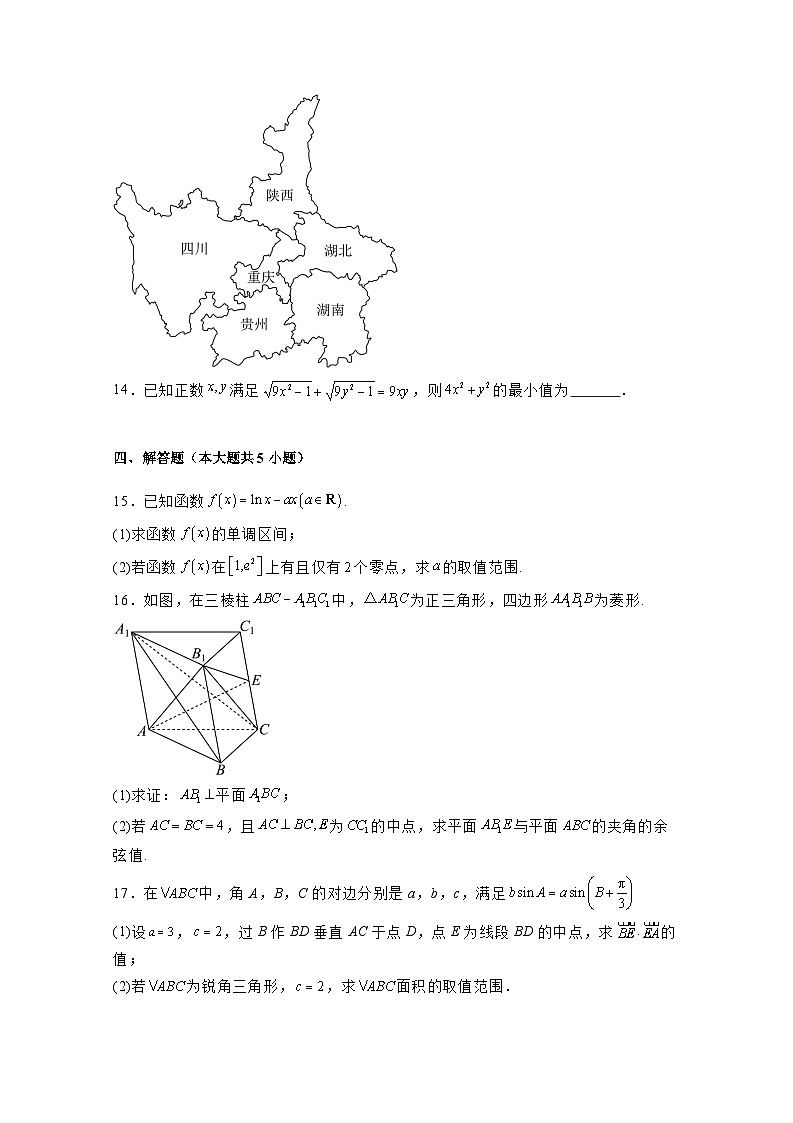
A．B．C．D．
6．已知函数（且）在定义域内是增函数，则的取值范围是（ ）
A．B．C．D．
7．已知函数，若为偶函数；且在区间内仅有两个零点，则的值是（ ）
A．2B．3C．5D．8
8．是定义在上的函数，，且对任意，满足，，则（ ）
A．2015B．2016C．2017D．2018
二、多选题（本大题共3小题）
9．设函数，则（ ）
A．有三个零点B．是的极小值点
C．的图象关于点对称D．当时，
10．李明每天7：00从家里出发去学校，有时坐公交车，有时骑自行车．他各记录了50次坐公交车和骑自行车所花的时间，经数据分析得到：坐公交车平均用时30分钟，样本方差为36；自行车平均用时34分钟，样本方差为4．假设坐公交车用时X和骑自行车用时Y都服从正态分布，则（ ）
A．P(X＞32)＞P(Y＞32)
B．P(X≤36)＝P(Y≤36)
C．李明计划7：34前到校，应选择坐公交车
D．李明计划7：40前到校，应选择骑自行车
11．已知中，，，E，F分别在线段BA，CA上，且，．现将沿EF折起，使二面角的大小为．以下命题正确的是（ ）
A．若，，则点到平面的距离为
B．存在使得四棱锥有外接球
C．若，则棱锥体积的最大值为
D．若，三棱锥的外接球的半径取得最小值时，
三、填空题（本大题共3小题）
12．已知等差数列的前n项和为，若，，则 ．
13．如下图，用4种不同颜色标注地图中的6个区域，相邻省颜色不同，有 种不同的涂色方式.
14．已知正数满足，则的最小值为 ．
四、解答题（本大题共5小题）
15．已知函数.
(1)求函数的单调区间；
(2)若函数在上有且仅有个零点，求的取值范围.
16．如图，在三棱柱中，为正三角形，四边形为菱形.
(1)求证：平面；
(2)若，且为的中点，求平面与平面的夹角的余弦值.
17．在中，角A，B，C的对边分别是a，b，c，满足
(1)设，，过B作BD垂直AC于点D，点E为线段BD的中点，求的值；
(2)若为锐角三角形，，求面积的取值范围．
18．已知M为圆上一个动点，垂直x轴，垂足为N，O为坐标原点，的重心为G.
(1)求点G的轨迹方程；
(2)记（1）中的轨迹为曲线C，直线与曲线C相交于A，B两点，点，若点恰好是的垂心，求直线的方程.
19．龙泉游泳馆为给顾客更好的体验，推出了A和B两个套餐服务，顾客可选择A和B两个套餐之一，并在App平台上推出了优惠券活动，下表是该游泳馆在App平台10天销售优惠券情况．
经计算可得.
(1)因为优惠券购买火爆，App平台在第10天时系统出现异常，导致当天顾客购买优惠券数量大幅减少，已知销售量y和日期t呈线性关系，现剔除第10天数据，求y关于t的经验回归方程结果中的数值用分数表示；
(2)若购买优惠券的顾客选择A套餐的概率为，选择B套餐的概率为，并且A套餐可以用一张优惠券，B套餐可以用两张优惠券，记App平台累计销售优惠券为n张的概率为，求；
(3)记（2）中所得概率的值构成数列.
①求的最值；
②数列收敛的定义：已知数列，若对于任意给定的正数，总存在正整数，使得当时，，（是一个确定的实数），则称数列收敛于.根据数列收敛的定义证明数列收敛．
参考公式.
答案
1．【正确答案】B
【详解】，∴．
故选：B．
2．【正确答案】D
【详解】由得：，即，
所以.
故选：D
3．【正确答案】C
【分析】解法一：由的坐标，求得的坐标，利用向量垂直的坐标表示式列出方程求解即得；解法二：先由化简，再代入的坐标计算即得.
【详解】解法一：由，，得．
由，得，即，解得．
解法二：由，得，即，
将代入，得，解得．
故选C．
4．【正确答案】C
【详解】因为，，
所以，解得，
所以，
故选：C
5．【正确答案】B
【详解】轴截面为等腰三角形，底边长为，设圆锥的高为，
则，解得，
故圆锥的体积为.
故选：B
6．【正确答案】C
【详解】由函数 ，
因为函数在定义域内是增函数，则满足，
解得，即实数的取值范围为.
故选：C．
7．【正确答案】A
【详解】，为偶函数，
所以，，，，
当x∈0,π，，因为在区间0,π内仅有两个零点，
所以，得，则.
故选：A
8．【正确答案】D
【详解】解：
三是相加得：，
又，
则，当且仅当时等号成立，
，
故选：D.
9．【正确答案】BD
【详解】A. ，得和1，所以函数有2个零点，故A错误；
B.，得和，
当或时，，当时，，
所以函数的单调递增区间是和，单调递减区间是，所以是的极小值，故B正确；
C.，不恒等于4，故C错误；
D.当时，单调递增，，所以，故D正确.
故选：BD
10．【正确答案】BCD
【详解】A.由条件可知，，根据对称性可知，故A错误；
B., ，所以，故B正确；
C. =，所以，故C正确；
D. ，，所以，故D正确.
故选：BCD
11．【正确答案】ACD
【详解】，，易知平面ABC,平面，
易知面
故点到平面的距离为即为点到平面的距离，
因为，所以，所以，
所以为二面角的平面角，
又为平面内两条相交直线，
所以平面，
所以平面，又在平面内，
所以平面平面，
所以到平面ABC的距离即为到，
A选项：，，即，三角形等边三角形，
可得：到的距离为，故A正确；
B选项：由于直角梯形不可能共圆，所以四棱锥无外接球，所以B错误；
C选项：由题意可知，，，
,
，
由基本不等式可知：，
当且仅当，即时取得最大值，
所以,
所以当，时，体积取到最大值，故正确；
D选项：由题意可知，，，
，也即两两垂直，
可以依次构造长方体，长方体的体对角线即为外接球的直径，设外接球半径为r，
则，，
所以时，取得最小值，此时，所以D正确．
故选：ACD
12．【正确答案】
【分析】利用等差数列的通项公式列式求得，再利用等差数列的求和公式即可得解.
【详解】设等差数列的公差为，
则有,解得：，
所以.
故答案为.
13．【正确答案】120
【详解】当陕西和贵州相同，陕西和贵州4种颜色，重庆3种颜色，四川有2种颜色，湖北有2种颜色，湖南有1种颜色，则共有种方法，
当陕西和贵州不同，湖北和贵州相同，则陕西有4种颜色，重庆3种颜色，贵州和湖北有2种颜色，湖南有2种颜色，四川有1种颜色，则共有种方法，
当陕西和贵州不同，湖北和贵州不同，则陕西有4种颜色，重庆3种颜色，贵州有2种颜色，湖北有1种颜色，湖南有1种颜色，四川有1种则共有种方法，
综上可知有种方法.
故120
14．【正确答案】1
【详解】由，得，
记，其中，
原不等式化为，所以，
所以，即．
所以，
当且仅当，即时取“”，所以的最小值为1．
故1．
15．【正确答案】(1)见解析
(2)
【详解】（1）因为函数，则，
当时，，函数在上单调递增；
当时，由可得，
若，则；若，则.
当时，函数的单调增区间为，单调减区间为，
综上所述，当时，函数的单调增区间为；
当时，函数的单调增区间为，单调减区间为.
（2）当时，由，可得，则直线与函数的图象有两个交点，
函数的定义域为，，
由，可得，
当时，，此时函数单调递增，
当时，，此时函数单调递减，
所以，函数的极大值为，且，，如下图所示：

由图可知，当时，
直线与函数在上的图象有两个交点，
因此，实数的取值范围是.
16．【正确答案】(1)证明见解析；
(2).
【详解】（1）设与交于点G，连接，
则由为正三角形可得，
又由四边形为菱形可得，
因为，平面，
所以平面.
（2）由（1）可得，
又，，平面，所以平面，
取中点，连接，则由为正三角形可得，
因为，所以，
又平面，平面，所以，
取中点，连接，则，故且，
故可建立如图所示的空间直角坐标系，
则，
所以，
由上是平面的一个法向量，
设平面的一个法向量为，
则，取，则，
设平面与平面的夹角为，
则，
所以平面与平面的夹角的余弦值为.
17．【正确答案】(1)；
(2).
【分析】（1）根据正弦定理求出，进而由余弦定理求出，利用三角形面积公式得，利用平面向量基本定理及数量积运算法则得到答案；
（2）由正弦定理得到，利用锐角三角形，求得，进而求出，由面积公式求得.
【详解】（1），由正弦定理得：
，
所以，
因为，所以，
所以，即，
因为，所以，
因为，，由余弦定理得：，
因为，所以，
其中，
所以，
因为点E为线段BD的中点，所以，
由题意得：，
所以.
（2）由（1）知：，又，
由正弦定理得：，
所以，
因为为锐角三角形，所以，解得：，
则，，，
故，
面积为
故面积的取值范围是.
18．【正确答案】(1)
(2)
【分析】（1）设，根据为的重心，得，代入，化简即可求解.
（2）根据垂心的概念求得，设直线方程，与椭圆联立，根据韦达定理，并利用，得，将韦达定理代入化简即可求解.
【详解】（1）设，则，因为为的重心，
故有，解得，代入，化简得，
又，故，所以的轨迹方程为.
（2）因为为的垂心，故有，
又，所以，故设直线的方程为，
与联立消去，得，
由，得，
设，则，
由，得，所以，
所以，
所以，化简得，
解得（舍去）或（满足），故直线的方程为.
19．【正确答案】(1)
(2)
(3)①最大值为，最小值为；②证明见解析
【分析】（1）计算出新数据的相关数值，代入公式求出的值，进而得到y关于t的回归方程；
（2）由题意可知，其中，构造等比数列，再利用等比数列的通项公式求解；
（3）①分n为偶数和n为奇数两种情况讨论，结合指数函数的单调性求解；
②利用数列收敛的定义，准确推理、运算，即可得证．
【详解】（1）剔除第10天的数据，可得，
，
则，
所以，
可得，所以；
（2）由题意知，其中，
所以，
又由，
所以是首项为1的常数列，即，
所以，
又因为，
所以数列是首项为，公比为的等比数列，
故，所以；
（3）①当为偶数时，单调递减，
最大值为；
当为奇数时，单调递增，最小值为，
综上可得，数列的最大值为，最小值为；
②证明：对任意总存在正整数，其中表示取整函数，
当时，，
所以数列收敛.日期t
1
2
3
4
5
6
7
8
9
10
销售量千张
1.9
1.98
2.2
2.36
2.43
2.59
2.68
2.76
2.7
0.4