

湖南省长沙市浏阳市2024-2025学年八年级(上)期中 数学试卷(解析版)
展开
这是一份湖南省长沙市浏阳市2024-2025学年八年级(上)期中 数学试卷(解析版),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1. 甲骨文是我国的一种古代文字,下列甲骨文中,不是轴对称的是( )
A. B. C. D.
【答案】D
【解析】解:A选项中的图形是轴对称图形,故A选项不合题意;
B选项中的图形是轴对称图形,故B选项不合题意;
C选项中图形是轴对称图形,故C选项不合题意;
D选项中的图形不是轴对称图形,故D选项符合题意.
故选:D.
2. 若一个三角形的三个内角的度数之比为,则这个三角形是( )
A. 锐角三角形B. 直角三角形
C. 钝角三角形D. 锐角三角形或钝角三角形
【答案】B
【解析】解:设这个三角形的三个内角为,根据题意,得
,
解得,
∴,
所以这个三角形是直角三角形.
故选:B.
3. 下列长度的三条线段能组成三角形的是( )
A. ,,B. ,,
C. ,,D. ,,
【答案】B
【解析】解:A、,不能组成三角形,故A不符合题意;
B、,能组成三角形,故B符合题意;
C、,不能组成三角形,故C不符合题意;
D、,不能组成三角形,故D不符合题意.
故选:B.
4. 下列各图中,作边上的高,正确的是( )
A. B.
C. D.
【答案】D
【解析】解:A、是边上的高,不符合题意;
B、是边上的高,不符合题意;
C、是边上的高,不符合题意;
D、是边上的高,符合题意;
故选:D.
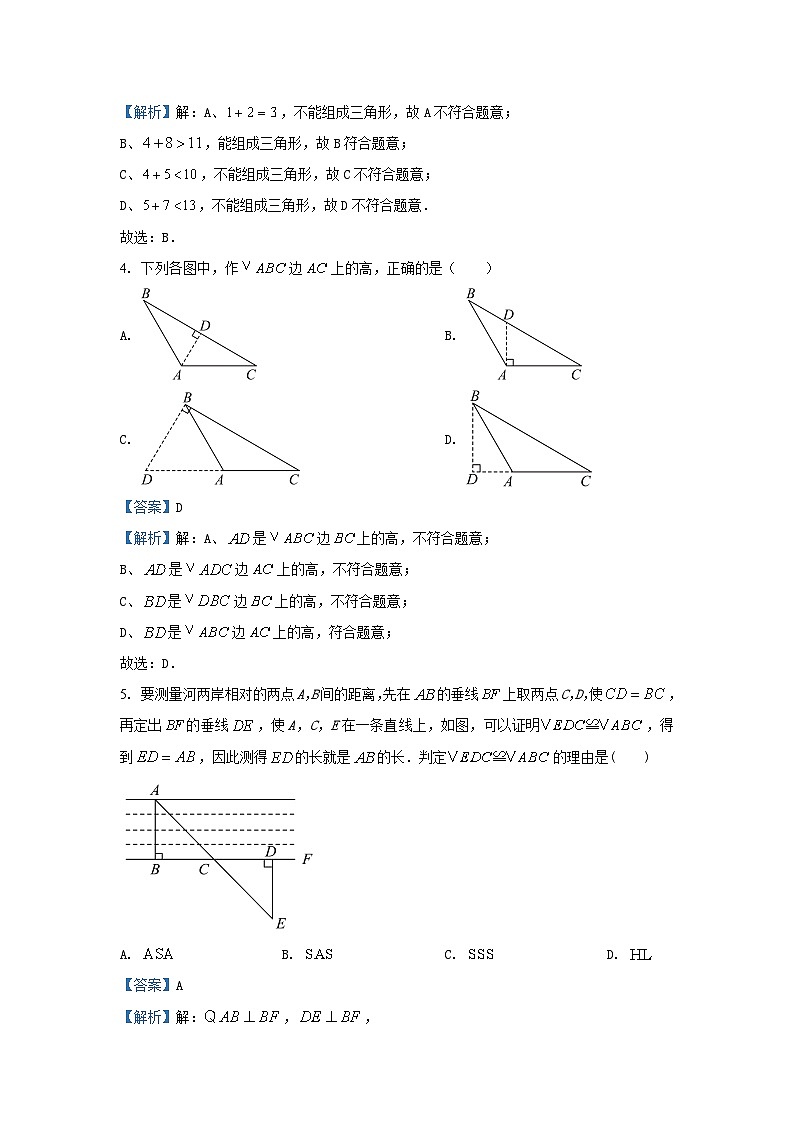
5. 要测量河两岸相对的两点A,B间的距离,先在的垂线上取两点C,D,使,再定出的垂线,使A,C,E在一条直线上,如图,可以证明,得到,因此测得的长就是的长.判定的理由是( )
A. B. C. D.
【答案】A
【解析】解:,,
,
和中,
,
,
∴,
故选:A.
6. 如图,已知,下列添加的条件不能使的是( )
A. B. C. D.
【答案】D
【解析】解:A、由,,添加条件,可以由证明,故此选项不符合题意;
B、由,,添加条件,可以由证明,故此选项不符合题意;
C、由,,添加条件,即,可以由证明,故此选项不符合题意;
D、由,,添加条件,不可以由证明,故此选项符合题意;
故选D.
7. 如图,一块直角三角板的60度的顶点A与直角顶点C分别在平行线上,斜边AB平分,交直线GH于点E,则的大小为( )
A. B. C. D.
【答案】C
【解析】∵AB平分,∠CAB=60,
∴∠DAE=60,
∵FD∥GH,
∴∠ACE+∠CAD=180,
∴∠ACE=180-∠CAB-∠DAE=60,
∵∠ACB=90,
∴∠ECB=90-∠ACE=30,
故选:C.
8. 如图所示,中,,,与相交于点,则的度数是( )
A. B. C. D.
【答案】D
【解析】解: 在和中,
,
,
,
,,
.
故选:D
9. 如图,在中,,是边上的高,,则下列结论中正确的是( )
A. B.
C. D.
【答案】D
【解析】解:∵在△ABC中,∠ACB=90°,
∴△ACB是直角三角形,
∵∠A=30°,
∴AB=2BC,
∵CD是AB边上的高,
∴∠CDA=90°,
∴∠ACD=60°,
∴∠DCB=30°,
∴BC=2BD.
故选:D.
10. 如图,是中的角平分线,于点,,,,则的长是( )
A. 4B. 5C. 6D. 7
【答案】D
【解析】解:如图,过点D作于点F,
∵是中的角平分线,,
∴,
∵,,,
∴.
故选:D.
二、填空题:(本题共6小题,每小题3分,共18分.)
11. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是______.
【答案】8
【解析】解:设边数为n,由题意得,
180(n-2)=3603,
解得n=8.
所以这个多边形的边数是8.
故答案为:8.
12. 已知点,与点关于x轴对称,则的值为_______.
【答案】
【解析】解:∵点,与点关于x轴对称,
∴,
∴,
故答案为:.
13. 如图,AB=AC,点D在AB上,点E在AC上,DC、EB交于点F,△ADC≌△AEB,只需增加一个条件,这个条件可以是______.
【答案】AD=AE
【解析】解:添加条件:AD=AE,
在△ABE和△ACD中,
∴△ADC≌△AEB(SAS),
故答案为AD=AE.
14. 等腰三角形的一个内角是,则它顶角的度数是______.
【答案】或
【解析】解:当是等腰三角形的顶角时,则顶角就是;
当是等腰三角形的底角时,则顶角是.
故答案为:或.
15. 如图,在三角形纸片中,,,.沿过点B的直线折叠这个三角形,使点C落在边上的点E处,折痕为,则的周长为____.
【答案】7
【解析】解:由折叠的性质得:,,
,
的周长,
故答案为:7.
16. 如图,中,的垂直平分线l与相交于点D,若的周长为,则_____.
【答案】12
【解析】解:∵l是的垂直平分线,
∴,
∵的周长为,,
∴,
∴,
∴,
故答案为:12.
三、解答题:(本大题共9个小题,第17、18、19题每小题6分,第20、21题每小题6分,第22、23题每小题6分,第24、25题每小题6分,共72分.解答应写出必要的文字说明、证明过程或演算步骤.)
17. 如图,在中,若,,,,求的度数.
解:,,
.
,,
,
.
18. 如图,,,.求证:.
解:证明:,
,即,
在和中,
,
,
.
19. 如图,在中,,点在边上,且,连接,若,求的度数.
解:设,
,
,
,
,
,
,
,
在中,
即,
,
.
20. 如图,三个顶点的坐标分别为,,.
(1)在图中作出关于y轴对称的图形;
(2)若P为x轴上一点,画出点P,使得的值最小;
(3)计算的面积.
解:(1)即为所求,如图:
;
(2)作点关于x轴对称的点,
由两点之间线段最短得:当点、、共线时,取得最小值,
连接,则,
的值最小,
点P即为所求;
(3) .
21. 把两个含有角的直角三角板如图放置,点D在上,连接,的延长线交于点F.
(1)求证:;
(2)若,求的长.
解:(1)证明:∵和都是等腰直角三角形,
∴,,,
在和中,
∵,
∴,
∴;
(2)解:∵,
∴①,
∵,
∴.
∵,
∴②,
∴由①、②得:.
22. 如图所示,点M是线段上一点,是过点M的一条直线,连接,过点B作交于F,且.
(1)若,求的长;
(2)若,求证:.
解:(1)解:∵,
∴,
∵,
∴,
∴,
∵,
∴;
(2)证明:∵,
∴,
∵,
∴,
∴,
∴,
在和中,
∵,
∴,
∴.
23. 如图,在中,平分交于点,过点作交于点.
(1)求证:是等腰三角形.
(2)若平分的周长,的周长为,求的周长.
解:(1)证明:平分,
,
,
,
,
为等腰三角形;
(2)解:的周长为15,
,
,
,
,
平分△的周长,
.
24. 如图,点O是等边内一点,.连接,.
(1)求证:是等边三角形;
(2)求的度数;
(3)探究:当为多少度时,是等腰三角形.
解:(1)证明:∵,
∴,,
,
是等边三角形,
,
,
∴是等边三角形;
(2)解:,
,
,
,
,
;
(3)解:当为或或时,是等腰三角形,
,
∴,
∴,
∵是等边三角形,
∴,
∴,
∵,
∴,
∴,
∵在中,,
∴,
∴,
∵是等腰三角形,
①当时,
∴,
∴,
∴;
②当时,
∴,
∴,
∴;
③当时,
∴,
∴,
∴,
∴当为或或时,是等腰三角形.
25. 如图1,在平面直角坐标系中,O为坐标原点,OA、OB、AB的长分别为a、b、c,且满足,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P运动时间为t秒.
(1)A的坐标为_________,B的坐标为_________.
(2)如图2,连结BP,当t为何值时,BP平分∠ABO.
(3)过P作PD⊥AB交直线AB于D,交y轴于Q,在点P运动的过程中,是否存在这样的点P,使POQ与AOB全等?若存在,请求出t的值;若不存在,请说明理由.
解:(1),
根据非负性得,
,
,
,,
故答案是:,;
(2)作,
平分,
,
,则,
,
即:,
,
,
当秒时,平分,
(3)如图,
当时,
,
,
,
,
,
,
当时,
,
同理可得:,
,
,
.
相关试卷
这是一份湖南省长沙市浏阳市2023-2024学年八年级(上)期末数学试卷(解析版),共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2024-2025学年湖南省长沙市浏阳市八年级(上)期中数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2024-2025学年湖南省长沙市浏阳市八年级(上)期中数学试卷,共6页。









