






所属成套资源:2024年人教版数学九年级上册同步课件
初中数学人教版(2024)九年级上册24.4 弧长和扇形面积优质ppt课件
展开
这是一份初中数学人教版(2024)九年级上册24.4 弧长和扇形面积优质ppt课件,共28页。PPT课件主要包含了C2πR,解得n≈90°,SπR2,∴OD=DC,又∵AD⊥DC,∴AC=AO=OC,有水部分的面积等内容,欢迎下载使用。
1.理解弧长和扇形面积公式的探求过程.(难点)2.会利用弧长和扇形面积的计算公式进行计算.(重点)
图为2020年8月3日,2020东京奥运会女子800米决赛起跑前的场景.为什么运动员的起跑线不在同一处?
因为要保证这些弯道的“展直长度”(弧长)是一样的.
怎样来计算弯道的“展直长度”(弧长)?
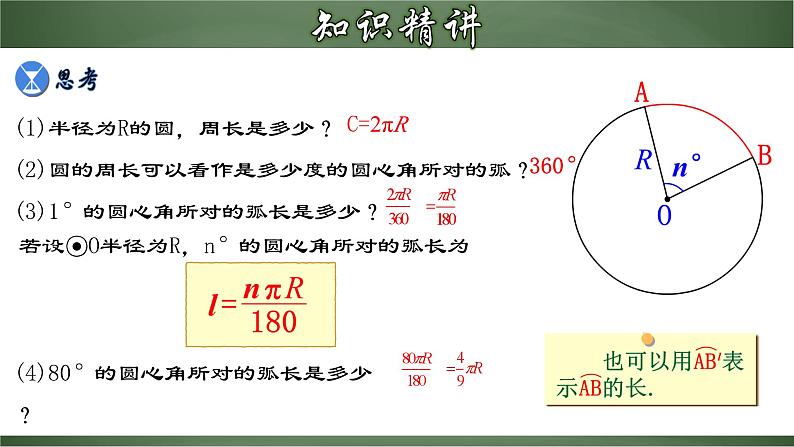
(1)半径为R的圆,周长是多少? (2)圆的周长可以看作是多少度的圆心角所对的弧?(3)1°的圆心角所对的弧长是多少?
(4)80°的圆心角所对的弧长是多少?
若设⊙O半径为R,n°的圆心角所对的弧长为
例1.制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算图中的管道的展直长度L(结果取整数).
解:由弧长公式,可得 的长 (mm) 因此所要求的展直长度L=2×700+1570=2970(mm)
解:设半径OA绕轴心O逆时针方向旋转的度数为n°.
因此,滑轮旋转的角度约为90°.
如图,由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形. (记作:扇形OAB)
扇形的面积除了与圆的半径有关外还与组成扇形的圆心角的大小有关.圆心角越大,扇形面积也就越大.怎样计算圆半径为R,圆心角为n°的扇形面积呢?
(1)半径为R的圆,面积是多少?(2)圆面可以看作是多少度的圆心角所对的扇形?(3)1°的圆心角所对的扇形面积是多少?
若设⊙O半径为R,n°的圆心角所对的扇形面积是
比较扇形面积公式和弧长公式,可以用弧长表示扇形的面积:
(其中l为扇形的弧长,R为半径.)
例2.如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(结果保留小数点后两位).
【分析】水面高0.3m是指哪一条线段的长?这条线段应该怎样画出来?要求图中阴影部分面积,应该怎么办?
过点O作OD垂直于AB并延长交圆O于C.线段DC.
阴影部分面积=扇形OAB的面积-△OAB的面积
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交圆于点C,连接AC.
∵ OC=0.6, DC=0.3,
∴ OD=OC- DC=0.3,
∴AD是线段OC的垂直平分线,
从而 ∠AOD=60˚, ∠AOB=120˚.
S=S扇形OAB - SΔOAB
如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.(结果保留小数点后两位).
解:如图,过点O作弦AB的垂线,垂足为D,交圆于点C
∵ 半径是0.6cm,水面高0.9cm,
∴ CD=0.9-0.6=0.3,
∴ OD=OC-DC=0.3
∴∠AOD=60˚, ∠AOB=120˚.
S=S扇形+SΔOAB
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
解:连接AD,由题意可得:AD= S阴影部分=S△ABC-3S扇形
解析:点A所经过的路线的长为三个半径为2,圆心角为120°的扇形弧长与两个半径为 ,圆心角为90°的扇形弧长之和,即
例5.如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.(1)求证:∠ACO=∠BCP;(2)若∠ABC=2∠BCP,求∠P的度数;(3)在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).
例5.如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.(1)求证:∠ACO=∠BCP;
(1)证明:∵AB是半圆O的直径,∴∠ACB=90°,∵CP是半圆O的切线,∴∠OCP=90°,∴∠ACB=∠OCP,∴∠ACO=∠BCP;
例5.如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.(2)若∠ABC=2∠BCP,求∠P的度数;
(2)解:由(1)知∠ACO=∠BCP,∵∠ABC=2∠BCP,∴∠ABC=2∠ACO,∵OA=OC,∴∠ACO=∠A,∴∠ABC=2∠A,∵∠ABC+∠A=90°,∴∠A=30°,∠ABC=60°,∴∠ACO=∠BCP=30°,∴∠P=∠ABC﹣∠BCP=60°﹣30°=30°,
例5.如图,C是圆O被直径AB分成的半圆上一点,过点C的圆O的切线交AB的延长线于点P,连接CA,CO,CB.(3)在(2)的条件下,若AB=4,求图中阴影部分的面积(结果保留π和根号).
1.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )A.3π B.4π C.5π D.6π 2.在半径为1的☉O中,弦AB=1,则 的长是( )A. B. C. D.3.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( ) A. B. C. D. 4.如果扇形的圆心角为150°,扇形面积为240πcm2,那么扇形的弧长为( )A.5πcm B.10πcm C.20πcm D.40πcm
7.☉O中,半径R=30cm, 的长度是8πcm,则 所对的圆心角是_____.8.☉O中,108°的圆心角所对的弧长是12πcm,则☉O的半径R=_____cm.9.半径为6cm,圆心角为40°的扇形面积是______cm2.10.扇形的弧长为2πcm,半径为3cm,则扇形面积为______cm2.
11.如图,圆心角为90°的扇形ACB内,以BC为直径作半圆,连接AB.若阴影部分的面积为π-1,则AC=_____.
相关课件
这是一份人教版九年级上册24.4 弧长和扇形面积集体备课课件ppt,共6页。PPT课件主要包含了扇形的定义和面积公式,知识点2,圆心角等内容,欢迎下载使用。
这是一份初中数学人教版九年级上册24.4 弧长及扇形的面积完整版ppt课件,文件包含244弧长和扇形面积-1课件pptx、人教版九年级数学上册244《弧长和扇形面积》第1课时教案doc、人教版九年级数学上册244《弧长和扇形面积》第1课时达标题doc、人教版九年级数学上册244《弧长和扇形面积》第1课时学案doc等4份课件配套教学资源,其中PPT共5页, 欢迎下载使用。
这是一份初中数学人教版九年级上册第二十四章 圆24.4 弧长和扇形面积说课课件ppt,共35页。PPT课件主要包含了知识回顾,学习目标,课堂导入,计算弯道对应的弧长,知识点1,新知探究,C2πR,弧长公式,跟踪训练,解得R15等内容,欢迎下载使用。









