
数学九年级上册2.8 圆锥的侧面积课时作业
展开知识点一
与圆锥相关的概念
◆1、圆锥:圆锥是一个底面和一个侧面围成的几何体.圆锥还可以看成由一个直角三角形绕它的一条直角边所在的直线旋转一周形成的图形.
◆2、圆锥的母线:我们把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线.圆锥有无数条母线,它们都相等.
◆3、圆锥的高:从圆锥的顶点到圆锥底面圆心之间的距离是圆锥的高.
◆4、重要的数量关系
如果用r表示圆锥底面的半径, h表示圆锥的高线长, l表示圆锥的母线长,那么r、h、l 之间数量关系是:由勾股定理得:r2+h2= l2,利用这一关系,已知任意两个量,可以求出第三个量.
知识点二
圆锥的侧面积和全面积
◆1、圆锥其侧面展开图扇形的半径=母线的长l
侧面展开图扇形的弧长=底面周长
◆2、圆锥的侧面积计算公式:S侧=12•2πr•l=π r l
◆3、圆锥的全面积计算公式:S全=S底+S侧=πr2+π r l
题型一 求圆锥的侧面积
【例题1】(2023•鹿城区校级三模)已知圆锥的底面半径是4,母线长是5,则圆锥的侧面积是( )
A.10πB.15πC.20πD.25π
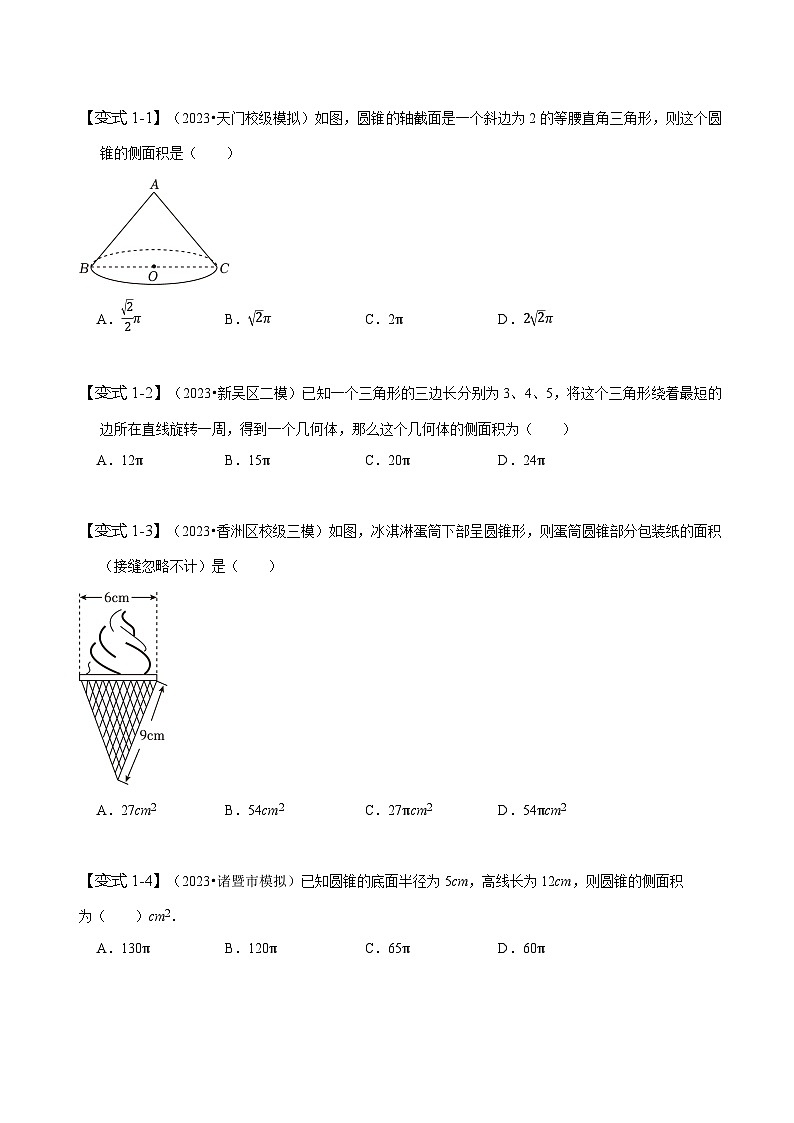
【变式1-1】(2023•天门校级模拟)如图,圆锥的轴截面是一个斜边为2的等腰直角三角形,则这个圆锥的侧面积是( )
A.22πB.2πC.2πD.22π
【变式1-2】(2023•新吴区二模)已知一个三角形的三边长分别为3、4、5,将这个三角形绕着最短的边所在直线旋转一周,得到一个几何体,那么这个几何体的侧面积为( )
A.12πB.15πC.20πD.24π
【变式1-3】(2023•香洲区校级三模)如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是( )
A.27cm2B.54cm2C.27πcm2D.54πcm2
【变式1-4】(2023•诸暨市模拟)已知圆锥的底面半径为5cm,高线长为12cm,则圆锥的侧面积
为( )cm2.
A.130πB.120πC.65πD.60π
【变式1-5】如图,已知一个圆锥的侧面展开图是一个半径为9cm,圆心角为120°的扇形.求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
题型二 求圆锥底面圆的半径
【例题2】(2023•娄星区一模)已知圆锥的母线长为20cm,其侧面展开图是圆心角为216°的扇形,则圆锥的底面半径长为( )
A.4πcmB.5πcmC.12cmD.15cm
【变式2-1】已知扇形AOB的半径为3cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的底面半径为( )
A.1cmB.2cmC.4cmD.8cm
【变式2-2】(2023•聊城一模)如图,已知Rt△ABC的∠A=90°,AB=AC=4,以点B为圆心,BA为半径,作AE交BC于点E.若扇形ABE恰好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径
是( )
A.12B.1C.22D.2
【变式2-3】如图,在边长为4的正方形内部裁得一个扇形BAC,若将该扇形围成一个圆锥,则此圆锥的底面半径为( )
A.1B.2C.32D.2
【变式2-4】(2023•耿马县一模)小科同学将一张直径为16的圆形卡纸平均分成4份,用其中一份作一个圆锥的侧面,则这个圆锥的底面半径是( )
A.2B.4C.8D.16
【变式2-5】如图所示,扇形OAB的面积为4πcm2,∠AOB=90°,用这个扇形围成一个圆锥的侧面.求这个圆锥的底面圆的半径.
题型三 求圆锥的高
【例题3】(2023•红塔区模拟)将一个直角三角形以一条直角边所在的直线为轴旋转一周,得到一个圆锥,若这个直角三角形斜边的长为13cm,圆锥的侧面积为65πcm2,则该圆锥的高为( )
A.5cmB.12cmC.13cmD.69cm
【变式3-1】(2023•上杭县模拟)圆锥的侧面展开图是一个圆心角120°,半径6cm的扇形,则该圆锥的高是( )
A.1cmB.2cmC.42cmD.210cm
【变式3-2】(2022•西双版纳模拟)如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画弧,则由图中阴影部分的扇形围成的圆锥的高为( )
A.42B.26C.33D.4
【变式3-3】如图,从一块直径是4m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )
A.22mB.15mC.302mD.30m
【变式3-4】如果从半径为5cm的圆形纸片上剪去15圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),求这个圆锥的高.
【变式3-5】已知如图,扇形AOB的圆心角为120°,半径OA为9cm.
(1)求扇形AOB的弧长和扇形面积;
(2)若把扇形纸片AOB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.
题型四 求圆锥的母线长
【例题4】(2022春•舟山月考)圆锥的底面半径为4,侧面展开图扇形的圆心角为120°,则该圆锥的母线长为( )
A.6B.12C.18D.24
【变式4-1】(2023•如皋市一模)已知圆锥的侧面积为10πcm2,底面圆的半径为2cm,则该圆锥的母线长为 cm.
【变式4-2】(2022秋•句容市期中)某同学在数学实践活动中,制作了一个侧面积为40π,底面半径为4的圆锥模型,则此圆锥的母线长为 .
【变式4-3】(2023•吴忠模拟)如图所示,圆锥形烟囱帽的底面半径为12cm,侧面展开图为半圆形,则它的母线长为 .
【变式4-4】(2023•温州模拟)已知圆锥的底面半径为2cm,表面积为14πcm2,则该圆锥的母线长
为 cm.
题型五 圆锥的侧面展开图的圆心角
【例题5】若一个圆锥的底面半径为3cm,高为62cm,则圆锥的侧面展开图中圆心角的度数为( )
A.150°B.120°C.100°D.80°
【变式5-1】(2022秋•枣阳市期末)某学校组织开展手工制作实践活动,一学生制作的圆锥母线长为30cm,底面圆的半径为10cm,这个圆锥的侧面展开图的圆心角度数是( )
A.30°B.60°C.90°D.120°
【变式5-2】(2023•盱眙县模拟)若要制作一个母线长为9cm,底面圆的半径为4cm的圆锥,则这个圆锥的侧面展开图的圆心角度数是 .
【变式5-3】若一个圆锥的底面圆的半径是52,母线长8,则该圆锥的侧面展开图的圆心角度数是 .
【变式5-4】(2023•仙桃校级一模)已知圆锥底面圆的周长为2π,圆锥的母线为3,则该圆锥的侧面展开图的圆心角为 .
题型六 圆锥计算与实际应用问题
【例题6】(2023•海州区二模)如图,一把打开的雨伞可近似的看成一个圆锥,伞骨(面料下方能够把面料撑起来的支架)末端各点所在圆的直径AC长为12分米,伞骨AB长为10分米,那么制作这样的一把雨伞至少需要绸布面料为 平方分米.
【变式6-1】如图,粮仓的顶部是圆锥形状,这个圆锥底面的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是( )
A.540π元B.360π元C.180π元D.90π元
【变式6-2】(2023•洪雅县模拟)如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.(30+529)π米2B.40π米2
C.(30+521)π米2D.55π米2
【变式6-3】如图,粮仓的顶部是圆锥形状,这个圆锥的底面圆的半径为3米,母线长为6米,为防雨水,需要在粮仓顶部铺上油毡,如果油毡的市场价为10元/米2,那么购买油毡所需要的费用是 元(结果保留π).
【变式6-4】如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.
(1)求剪下的扇形ABC(即阴影部分)的半径;
(2)若用此剪下的扇形铁皮围成一个圆锥形铁帽,求此圆锥形铁帽的底面圆的半径r.
【变式6-5】下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
题型七 圆锥与最短距离
【例题7】如图,已知圆锥的底面半径为r=20cm,h=2015cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,则蚂蚁爬行的最短距离是( )cm.
A.40B.40πC.160D.802
【变式7-1】(2022秋•沙坪坝区校级期中)如图1,一只蚂蚁从圆锥底端点A出发,绕圆锥表面爬行一周后回到点A,将圆锥沿母线OA剪开,其侧面展开图如图2所示,若∠AOA′=120°,OA=3,则蚂蚁爬行的最短距离是 .
【变式7-2】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为5cm,母线OE(OF)长为5cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离为 cm.
【变式7-3】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.
(1)求圆锥形纸杯的侧面积.
(2)若在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,求此蚂蚁爬行的最短距离.
(苏科版)九年级上册数学《第2章 对称图形---圆》
2.8 圆锥的侧面积
知识点一
与圆锥相关的概念
◆1、圆锥:圆锥是一个底面和一个侧面围成的几何体.圆锥还可以看成由一个直角三角形绕它的一条直角边所在的直线旋转一周形成的图形.
◆2、圆锥的母线:我们把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线.圆锥有无数条母线,它们都相等.
◆3、圆锥的高:从圆锥的顶点到圆锥底面圆心之间的距离是圆锥的高.
◆4、重要的数量关系
如果用r表示圆锥底面的半径, h表示圆锥的高线长, l表示圆锥的母线长,那么r、h、l 之间数量关系是:由勾股定理得:r2+h2= l2,利用这一关系,已知任意两个量,可以求出第三个量.
知识点二
圆锥的侧面积和全面积
◆1、圆锥其侧面展开图扇形的半径=母线的长l
侧面展开图扇形的弧长=底面周长
◆2、圆锥的侧面积计算公式:S侧=12•2πr•l=π r l
◆3、圆锥的全面积计算公式:S全=S底+S侧=πr2+π r l
题型一 求圆锥的侧面积
【例题1】(2023•鹿城区校级三模)已知圆锥的底面半径是4,母线长是5,则圆锥的侧面积是( )
A.10πB.15πC.20πD.25π
【分析】根据圆锥的侧面展开图是扇形、扇形的面积公式计算,得到答案.
【解答】解:圆锥的侧面积=12×2π×4×5=20π,
故选:C.
【点评】本题考查的是圆锥的计算,理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键.
【变式1-1】(2023•天门校级模拟)如图,圆锥的轴截面是一个斜边为2的等腰直角三角形,则这个圆锥的侧面积是( )
A.22πB.2πC.2πD.22π
【分析】首先可求得圆锥的底面半径及母线长,再根据圆锥的侧面积公式,即可求得.
【解答】解:∵圆锥的轴截面是一个斜边为2的等腰直角三角形,
∴底面半径=1,母线长AB=AC=2,底面周长=2π,
∴圆锥的侧面积=12×2π×2=2π,
故选:B.
【点评】本题考查了圆锥的侧面积计算,利用了圆的周长公式和扇形面积公式求解,解题的关键是牢记有关公式.
【变式1-2】(2023•新吴区二模)已知一个三角形的三边长分别为3、4、5,将这个三角形绕着最短的边所在直线旋转一周,得到一个几何体,那么这个几何体的侧面积为( )
A.12πB.15πC.20πD.24π
【分析】先根据勾股定理的逆定理可知为直角三角形,以直角边为3所在直线旋转一周得到一个圆锥,底面半径是4,母线是5,然后利用扇形的面积公式计算即可.
【解答】解:∵32+42=52,
∴这个三角形为直角三角形,两直角边为3,4,斜边为5,
∴以直角边为3所在直线旋转一周得到一个圆锥,底面半径是4,母线是5,
∴12×2π×4×5=20π.
故选:C.
【点评】此题考查了点、线、面、体中的面动成体,勾股定理的逆定理和圆锥的计算,解题关键是熟练运用公式.
【变式1-3】(2023•香洲区校级三模)如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(接缝忽略不计)是( )
A.27cm2B.54cm2C.27πcm2D.54πcm2
【分析】由于锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,所以根据扇形的面积公式可计算出蛋筒圆锥部分包装纸的面积
【解答】解:根据题意,圆锥的侧面积=12×2π×3×9=27(cm2),
即蛋筒圆锥部分包装纸的面积为27cm2.
故选:C.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
【变式1-4】(2023•诸暨市模拟)已知圆锥的底面半径为5cm,高线长为12cm,则圆锥的侧面积
为( )cm2.
A.130πB.120πC.65πD.60π
【分析】先利用勾股定理求得圆锥的母线长,再根据圆锥的侧面积=底面周长×母线长÷2列式计算即可.
【解答】解:∵圆锥的底面半径为5cm,高线长为12cm,
∴圆锥的底面周长=2π×5=10π(cm),母线长=52+122=13(cm),
∴圆锥的侧面积=12×10π×13=65π(cm2).
故选:C.
【点评】本题考查了圆锥的计算,利用了勾股定理,圆的周长公式和扇形面积公式求解.
【变式1-5】如图,已知一个圆锥的侧面展开图是一个半径为9cm,圆心角为120°的扇形.求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
【分析】(1)设该圆锥底面圆的半径为rcm,则可根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=120π×9180,然后解方程即可.
(2)计算圆锥的侧面积和底面面积,则可得出答案.
【解答】解:(1)设该圆锥底面圆的半径为rcm,
根据题意得2πr=120π×9180,
解得r=3,
即该圆锥底面圆的半径为3cm.
(2)∵该圆锥的侧面面积=120⋅π⋅92360=27π(cm2),
圆锥的底面面积=π•32=9π(cm2),
∴圆锥的全面积为27π+9π=36π(cm2).
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了扇形面积公式.
题型二 求圆锥底面圆的半径
【例题2】(2023•娄星区一模)已知圆锥的母线长为20cm,其侧面展开图是圆心角为216°的扇形,则圆锥的底面半径长为( )
A.4πcmB.5πcmC.12cmD.15cm
【分析】根据展开图的扇形弧长是圆锥底面圆的周长进行求解即可.
【解答】解:设圆锥的底面半径长为rcm,
∵圆锥的母线长为20cm,其侧面展开图是圆心角为216°的扇形,
∴2πr=216×π×20180,
解得:r=12,
∴圆锥的底面半径长为12cm,
故选:C.
【点评】本题主要考查了求圆锥底面圆半径,熟知展开图的扇形弧长是圆锥底面圆的周长是解题的关键.
【变式2-1】已知扇形AOB的半径为3cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则围成的圆锥的底面半径为( )
A.1cmB.2cmC.4cmD.8cm
【分析】首先利用扇形的弧长公式即可求得扇形,然后根据圆的周长公式即可求解.
【解答】解:扇形的弧长是120×3π180=2π(cm),
设底面半径是rcm,
则2πr=2π,
解得:r=1.
故选:A.
【点评】本题考查圆锥的计算,理解圆锥的展开图中扇形的弧长等于圆锥的底面周长是关键.
【变式2-2】(2023•聊城一模)如图,已知Rt△ABC的∠A=90°,AB=AC=4,以点B为圆心,BA为半径,作AE交BC于点E.若扇形ABE恰好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径是( )
A.12B.1C.22D.2
【分析】根据圆锥的底面周长与展开后所得扇形的弧长相等列式计算即可.
【解答】解:设圆锥的底面圆的半径为r,
根据题意可知:AB=BE=4,∠ABE=45°,
底面圆的周长等于弧长,
∴2πr=45×π×4180,
解得r=12,
该圆锥的底面圆的半径是12,
故选:A.
【点评】本题考查了圆锥的计算,解决本题的关键是掌握圆锥的底面周长与展开后所得扇形的弧长相等.
【变式2-3】如图,在边长为4的正方形内部裁得一个扇形BAC,若将该扇形围成一个圆锥,则此圆锥的底面半径为( )
A.1B.2C.32D.2
【分析】根据扇形的弧长等于圆锥的底面周长求得半径即可.
【解答】解:设圆锥的底面半径为r,
根据题意得:2πr=2×4π4,
解得:r=1,
故选:A.
【点评】考查了圆锥的计算,解题的关键是了解圆锥的底面周长等于扇形的弧长,难度不大.
【变式2-4】(2023•耿马县一模)小科同学将一张直径为16的圆形卡纸平均分成4份,用其中一份作一个圆锥的侧面,则这个圆锥的底面半径是( )
A.2B.4C.8D.16
【分析】先求出圆形卡纸的周长,再求出圆锥的底面圆的周长,最后根据圆的周长公式求出半径即可.
【解答】解:圆形卡纸的周长为16π,
∵16π4=4π,
∴圆锥的底面圆的周长为4π,
设圆锥的底面半径为r,
则2πr=4π,
解得:r=2,
即这个圆锥的底面半径为2,
故选:A.
【点评】本题考查了圆锥的计算,能求出圆锥的底面圆的周长是解此题的关键.
【变式2-5】如图所示,扇形OAB的面积为4πcm2,∠AOB=90°,用这个扇形围成一个圆锥的侧面.求这个圆锥的底面圆的半径.
【分析】设扇形的半径为Rcm,利用扇形的面积公式得到90×π×R2360=4π,解得R=4,再设这个圆锥的底面圆的半径为rcm,利用扇形面积公式得到12×2πr×4=4π,然后解关于r的方程即可.
【解答】解:设扇形的半径为Rcm,
根据题意得90×π×R2360=4π,
解得R=4(负值舍去),
设这个圆锥的底面圆的半径为rcm,
则12×2πr×4=4π,
解得r=1,
所以这个圆锥的底面圆的半径为1cm.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
题型三 求圆锥的高
【例题3】(2023•红塔区模拟)将一个直角三角形以一条直角边所在的直线为轴旋转一周,得到一个圆锥,若这个直角三角形斜边的长为13cm,圆锥的侧面积为65πcm2,则该圆锥的高为( )
A.5cmB.12cmC.13cmD.69cm
【分析】根据扇形面积公式求出圆锥的底面半径,再根据勾股定理计算,得到答案.
【解答】解:设圆锥的底面半径为rcm,
由题意得:12×2πr×13=65π,
解得:r=5,
则圆锥的高为:132−52=12(cm),
故选:B.
【点评】本题考查的是圆锥的计算,掌握扇形面积公式是解题的关键.
【变式3-1】(2023•上杭县模拟)圆锥的侧面展开图是一个圆心角120°,半径6cm的扇形,则该圆锥的高是( )
A.1cmB.2cmC.42cmD.210cm
【分析】利用弧长公式计算得出圆锥的底面周长,继而求得底面圆半径,再利用勾股定理求得高即可.
【解答】解:∵一圆锥的侧面展开图是圆心角为120°、半径为6cm的扇形,
∴扇形弧长=120π×6180=4π(cm),
∴2πr=4π,
∴r=2(cm),
∴圆锥的高=62−22=42(cm),
故选:C.
【点评】考查了圆锥的计算,用到的知识点为:扇形的弧长公式公式和勾股定理.
【变式3-2】(2022•西双版纳模拟)如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画弧,则由图中阴影部分的扇形围成的圆锥的高为( )
A.42B.26C.33D.4
【分析】首先确定扇形的圆心角的度数,然后利用圆锥的底面圆周长是扇形的弧长计算即可.
【解答】解:∵正六边形的外角和为360°,
∴每一个外角的度数为360°÷6=60°,
∴正六边形的每个内角为180°﹣60°=120°.
设这个圆锥底面圆的半径是r,
根据题意得,2πr=120π×6180,
解得,r=2.
∴圆锥的高为62−22=42,
故选:A.
【点评】本题考查了正多边形和圆及圆锥的计算的知识,解题的关键是求得正六边形的内角的度数并理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.此题难度不大.
【变式3-3】如图,从一块直径是4m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )
A.22mB.15mC.302mD.30m
【分析】连接AO,求出AB的长度,然后求出BC的弧长,进而求出扇形围成的圆锥的底面半径,应用勾股定理,求出圆锥的高.
【解答】解:连接AO,
∵AB=AC,点O是BC的中点,
∴AO⊥BC,
又∵∠BAC=90°,
∴∠ABO=∠AC0=45°,
∴AB=2OB=22(m),
∴BC的长为:90π×22180=2π(m),
∴剪下的扇形围成的圆锥的半径是:2π÷2π=22(m),
∴圆锥的高为:(22)2−(22)2=302(m),
故选:C.
【点评】此题主要考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
【变式3-4】如果从半径为5cm的圆形纸片上剪去15圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),求这个圆锥的高.
【分析】因为圆锥的高,底面半径,母线构成直角三角形,则留下的扇形的弧长=4×2π×55=8π,所以圆锥的底面半径r=4cm,利用勾股定理求圆锥的高即可
【解答】解:∵从半径为5cm的圆形纸片上剪去15圆周的一个扇形,
∴留下的扇形的弧长=4×2π×55=8π,
根据底面圆的周长等于扇形弧长,
∴圆锥的底面半径r=8π2π=4cm,
∴圆锥的高为52−42=3(cm).
【点评】此题主要考查了主要考查了圆锥的性质,要知道(1)圆锥的高,底面半径,母线构成直角三角形,(2)此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.解此类题目要根据所构成的直角三角形的勾股定理作为等量关系求解.
【变式3-5】已知如图,扇形AOB的圆心角为120°,半径OA为9cm.
(1)求扇形AOB的弧长和扇形面积;
(2)若把扇形纸片AOB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.
【分析】(1)根据弧长公式、扇形面积公式计算即可;
(2)根据扇形AOB的弧长求出圆锥的底面半径,根据勾股定理计算即可.
【解答】解:(1)扇形AOB的弧长=120π×9180=6π(cm),
S扇形AOB=120π×92360=27π(cm2);
(2)∵扇形AOB的弧长为6πcm,
∴圆锥的底面周长为6πcm,
∴圆锥的底面半径为3cm,
∴OH=92−32=62(cm).
【点评】本题考查的是圆锥的计算、弧长和扇形面积计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键.
题型四 求圆锥的母线长
【例题4】(2022春•舟山月考)圆锥的底面半径为4,侧面展开图扇形的圆心角为120°,则该圆锥的母线长为( )
A.6B.12C.18D.24
【分析】根据弧长公式计算,得到答案.
【解答】解:设圆锥的母线长为l,
∵圆锥的底面半径为4,
∴圆锥的底面周长为8π,
∴圆锥的侧面展开图扇形的弧长为8π,
则120πl180=8π,
解得:l=12,
∴圆锥的母线长为12,
故选:B.
【点评】本题考查的是圆锥的计算,熟记弧长公式是解题的关键.
【变式4-1】(2023•如皋市一模)已知圆锥的侧面积为10πcm2,底面圆的半径为2cm,则该圆锥的母线长为 cm.
【分析】圆锥的侧面积=底面周长×母线长÷2,把相应数值代入即可求解.
【解答】解:设圆锥的母线长为Rcm,
圆锥的底面周长=2π×2=4πcm,
则12×4π×R=10π,
解得,R=5(cm)
故答案为:5.
【点评】本题考查的是圆锥的计算,理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
【变式4-2】(2022秋•句容市期中)某同学在数学实践活动中,制作了一个侧面积为40π,底面半径为4的圆锥模型,则此圆锥的母线长为 .
【分析】设此圆锥的母线长为l,利用扇形的面积公式得到12×2π×4×l=40π,然后解方程即可.
【解答】解:如图,设此圆锥的母线长为l,根据题意得:12×2π×4×l=40π,
解得:l=10,
∴此圆锥的母线长为10.
故答案为:10.
【点评】本题考查圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.掌握圆锥的相关知识是解题的关键.
【变式4-3】(2023•吴忠模拟)如图所示,圆锥形烟囱帽的底面半径为12cm,侧面展开图为半圆形,则它的母线长为 .
【分析】根据弧长公式列方程求解即可.
【解答】解:设母线的长为R,
由题意得,πR=2π×12,
解得R=24,
∴母线的长为24cm,
故答案为:24cm.
【点评】本题主要考查弧长的计算,根据展开后的半圆弧长等于圆锥形烟囱帽的底面周长列方程求解是解题的关键.
【变式4-4】(2023•温州模拟)已知圆锥的底面半径为2cm,表面积为14πcm2,则该圆锥的母线长
为 cm.
【分析】根据圆的周长公式求出圆锥的底面周长,根据圆锥的表面积的计算公式构建方程求解即可.
【解答】解:设圆锥的母线长为Rcm,
圆锥的底面周长=2π×2=4π(cm),
则12×4π×R+π×22=14π,
解得,R=5,
故答案为:5.
【点评】本题考查的是圆锥的计算,理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
题型五 圆锥的侧面展开图的圆心角
【例题5】若一个圆锥的底面半径为3cm,高为62cm,则圆锥的侧面展开图中圆心角的度数为( )
A.150°B.120°C.100°D.80°
【分析】设圆锥的侧面展开图中圆心角的度数为n°,先利用勾股定理计算出圆锥的母线长为9,再利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2π×3=nπ×9180,然后解关于n的方程即可.
【解答】解:设圆锥的侧面展开图中圆心角的度数为n°,
圆锥的母线长为32+(62)2=9,
所以2π×3=nπ×9180,
解得n=120,
即圆锥的侧面展开图中圆心角的度数为120°,
故选:B.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
【变式5-1】(2022秋•枣阳市期末)某学校组织开展手工制作实践活动,一学生制作的圆锥母线长为30cm,底面圆的半径为10cm,这个圆锥的侧面展开图的圆心角度数是( )
A.30°B.60°C.90°D.120°
【分析】根据题意可知,圆锥的底面圆的周长=扇形的弧长,即可列出相应的方程,然后求解即可.
【解答】解:设这种圆锥的侧面展开图的圆心角度数是n°,
根据题意得,2π×10=nπ×30180,
解得n=120,
即这种圆锥的侧面展开图的圆心角度数是120°,
故选:D.
【点评】本题考查圆锥的计算,解答本题的关键是明确圆锥的底面圆的周长=扇形的弧长.
【变式5-2】(2023•盱眙县模拟)若要制作一个母线长为9cm,底面圆的半径为4cm的圆锥,则这个圆锥的侧面展开图的圆心角度数是 .
【分析】利用圆锥侧面展开图,扇形圆心角与母线和底面圆半径的关系计算,即可求解.
【解答】解:设这个圆锥的侧面展开图的圆心角的度数是n,
根据题意得:2π×4=nπ×9180,
解得n=160,
即这个圆锥的侧面展开图的圆心角是160°,
故答案为:160°.
【点评】本题考查了圆锥侧面展开图,扇形圆心角与母线和底面圆半径的关系,明确圆锥的底面圆的周长=扇形的弧长是解答本题的关键.
【变式5-3】若一个圆锥的底面圆的半径是52,母线长8,则该圆锥的侧面展开图的圆心角度数是 .
【分析】由题意可以得到圆锥侧面展开图的半径和弧长,然后可以求得圆锥侧面展开图的圆心角度数.
【解答】解:由题意可得:
圆锥侧面展开图的半径为8,圆锥侧面展开图的弧长为2π×52=5π,
∵nπ⋅8180=5π,
∴圆锥侧面展开图的圆心角度数是n=5π8π×180°=112.5°,
故答案为:112.5°.
【点评】本题考查圆的综合应用,熟练掌握圆锥侧面展开图的知识和圆心角的求法是解题关键.
【变式5-4】(2023•仙桃校级一模)已知圆锥底面圆的周长为2π,圆锥的母线为3,则该圆锥的侧面展开图的圆心角为 .
【分析】根据圆锥底面圆周长是其展开图的扇形弧长进行求解即可.
【解答】解:设该圆锥的侧面展开图的圆心角为n°,
由题意得,n⋅π⋅3180=2π,
∴n=120,
∴该圆锥的侧面展开图的圆心角为120°,
故答案为:120°.
【点评】本题主要考查了求圆锥侧面展开图的圆心角度数,熟知圆锥底面圆周长是其展开图的扇形弧长是解题的关键.
题型六 圆锥计算与实际应用问题
【例题6】(2023•海州区二模)如图,一把打开的雨伞可近似的看成一个圆锥,伞骨(面料下方能够把面料撑起来的支架)末端各点所在圆的直径AC长为12分米,伞骨AB长为10分米,那么制作这样的一把雨伞至少需要绸布面料为 平方分米.
【分析】圆锥的侧面展开图为扇形,根据题意可得该圆锥的母线长为AB,则扇形的直径为AC,根据AC的长度可求出圆锥地面周长,即可得出扇形的弧长,最后根据扇形面积公式S=12lr即可求解.
【解答】解:∵AC=12分米,
∴该圆锥底面周长为12π分米,
∴该圆锥侧面积=12×12π×10=60π(平方分米),
故答案为:60π.
【点评】本题主要考查了求圆锥侧面积,解题的关键是掌握圆锥的侧面展开图为扇形,以及扇形面积公式S=12lr.
【变式6-1】如图,粮仓的顶部是圆锥形状,这个圆锥底面的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是( )
A.540π元B.360π元C.180π元D.90π元
【分析】圆锥的侧面积=底面周长×母线长÷2.算出侧面积后乘以单价即可.
【解答】解:底面半径为3m,则底面周长=6π,侧面面积=12×6π×6=18π(m2).
所需要的费用=18π×10=180π(元),
故选:C.
【点评】本题利用了圆的周长公式和扇形面积公式求解,解题的关键是熟练掌握公式并正确的运用,难度不大.
【变式6-2】(2023•洪雅县模拟)如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.(30+529)π米2B.40π米2
C.(30+521)π米2D.55π米2
【分析】利用圆的面积得到底面圆的半径为5,再利用勾股定理计算出母线长,接着根据圆锥的侧面展开图为一扇形和圆柱的侧面展开图为矩形计算它们的侧面积,最后求它们的和即可.
【解答】解:∵底面圆的半径为5米,高为3米,
∴圆锥的母线长=22+52=29米,
所以圆锥的侧面积=12•2π•5•29=529π米;
圆柱的侧面积=2π•5•3=30π米2,
所以需要毛毡的面积=(30π+529π)米2.
故选:A.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
【变式6-3】如图,粮仓的顶部是圆锥形状,这个圆锥的底面圆的半径为3米,母线长为6米,为防雨水,需要在粮仓顶部铺上油毡,如果油毡的市场价为10元/米2,那么购买油毡所需要的费用是 元(结果保留π).
【分析】根据圆锥侧面积公式S=πrl,算出油毡的面积,乘以10即可得到结果.
【解答】解:根据题意得:圆锥侧面积=π×3×6=18π(平方米),
则购买油毡所需要的费用=10×18π=180π(元).
故答案为:180π.
【点评】此题考查了圆锥的计算,熟练掌握圆锥侧面积公式是解本题的关键.
【变式6-4】如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.
(1)求剪下的扇形ABC(即阴影部分)的半径;
(2)若用此剪下的扇形铁皮围成一个圆锥形铁帽,求此圆锥形铁帽的底面圆的半径r.
【分析】(1)连接OA,过点O作OD⊥AC于D,根据含30°角的直角三角形的性质求出OD,根据勾股定理求出AD,进而求出AC;
(2)根据圆的周长公式计算即可.
【解答】解:(1)连接OA,过点O作OD⊥AC于D,
则AD=DC,
∵∠BAC=60°,
∴∠OAD=30°,
∴OD=12OA=2,
∴AD=OA2−OD2=3,
∴AC=2AD=23,即剪下的扇形ABC(即阴影部分)的半径为23;
(2)扇形BAC的弧长为:60π×23180=23π3,
∴圆锥形铁帽的底面周长为23π3,
∴2πr=23π3,
解得:r=33.
【点评】本题考查了圆锥的计算,圆锥的侧面展开图为扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长,要熟记弧长公式和扇形的面积公式.
【变式6-5】下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
【分析】(1)设∠AOB=n°,AO=R,则CO=R﹣8,利用圆锥的侧面展开图扇形的弧长等于圆锥底面周长作为相等关系列方程,并联立成方程组求解即可;
(2)求纸杯的侧面积即为扇环的面积,需要用大扇形的面积减去小扇形的面积.纸杯表面积=S纸杯侧面积+S纸杯底面积.
【解答】解:由题意可知:BA=6π,CD=4π,设∠AOB=n,AO=R,则CO=R﹣8,
由弧长公式得:nπR180=6π,nπ(R−8)180=4π,
∴6×180=nR4×180=nR−8n,
解得:n=45,R=24,
故扇形OAB的圆心角是45度.
∵R=24,R﹣8=16,
∴S扇形OCD=12×4π×16=32π(cm2),
S扇形OAB=12×6π×24=72π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=72π﹣32π=40π(cm2),
纸杯底面积=π•22=4π(cm2)
纸杯表面积=40π+4π=44π(cm2).
【点评】主要考查圆锥的侧面展开图与底面周长之间的关系和扇环的面积的求法.
本题中(1)就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解;
(2)扇环的面积等于大扇形的面积减去小扇形的面积.
题型七 圆锥与最短距离
【例题7】如图,已知圆锥的底面半径为r=20cm,h=2015cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,则蚂蚁爬行的最短距离是( )cm.
A.40B.40πC.160D.802
【分析】蚂蚁爬行的最短距离是圆锥的展开图的扇形中AA′的长度.根据勾股定理求得母线长后,利用弧长等于底面周长求得扇形的圆心角的度数为90度,再由等腰直角三角形的性质求解.
【解答】解:设扇形的圆心角为n,圆锥的顶点为B,
∵r=20cm,h=2015cm,
∴由勾股定理可得母线l=r2+ℎ2=80(cm),
而圆锥侧面展开后的扇形的弧长为2×20π=nπ×80180,
∴n=90°,
即△BAA′是等腰直角三角形,
由勾股定理得:AA'=BA′2+BA2=802(cm).
∴蚂蚁爬行的最短距离为802cm.
故选:D.
【点评】本题利用了勾股定理,弧长公式,圆的周长公式,等腰直角三角形的性质求解.
【变式7-1】(2022秋•沙坪坝区校级期中)如图1,一只蚂蚁从圆锥底端点A出发,绕圆锥表面爬行一周后回到点A,将圆锥沿母线OA剪开,其侧面展开图如图2所示,若∠AOA′=120°,OA=3,则蚂蚁爬行的最短距离是 .
【分析】连接AA′,过O点作OH⊥AA′于H点,如图2,根据等腰三角形的性质得到AH=A′H,∠OAA′=30°,然后利用含30度角的直角三角形三边的关系计算出AH,从而得到AA′的长.
【解答】解:连接AA′,过O点作OH⊥AA′于H点,如图2,
∵OA=OA′,∠AOA′=120°,
∴AH=A′H,∠OAA′=30°,
在Rt△OAH中,∵OH=12OA=32,
∴AH=3OH=32×3=32,
∴AA′=2AH=3.
故答案为:3.
【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了最短路径问题.
【变式7-2】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为5cm,母线OE(OF)长为5cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离为 cm.
【分析】要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.
【解答】解:∵OE=OF=EF=5(cm),
∴底面周长=5π(cm),
将圆锥侧面沿OF剪开展平得一扇形,此扇形的半径OE=5(cm),弧长等于圆锥底面圆的周长5π(cm)
设扇形圆心角度数为n,则根据弧长公式得:
5π=5nπ180,
∴n=180,
即展开图是一个半圆,
∵E点是展开图弧的中点,
∴∠EOF=90°,
连接EA,则EA就是蚂蚁爬行的最短距离,
在Rt△AOE中由勾股定理得,
EA2=OE2+OA2=25+9=34,
∴EA=34(cm),
即蚂蚁爬行的最短距离是34cm.
故答案为:34.
【点评】考查了平面展开﹣最短路径问题,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
【变式7-3】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.
(1)求圆锥形纸杯的侧面积.
(2)若在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,求此蚂蚁爬行的最短距离.
【分析】(1)根据扇形的面积公式计算即可得到结果;
(2)要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,求出EA长即可,在Rt△EOA中,OA=8,0E=10,根据勾股定理求出AE,即可得出结果.
【解答】解:(1)S圆锥的侧面积=12×10×10π=50π;
(2)圆锥侧面沿母线OF展开可得下图:
则EF=圆锥底面周长的一半=12×10π=10nπ180,
∴n=90,即∠EOF=90°,
在Rt△AOE中,OA=8cm,OE=10cm,
根据勾股定理可得:AE=241cm,
所以蚂蚁爬行的最短距离为241cm.
【点评】本题考查了平面展开﹣最短路径问题,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.解题技巧提炼
直接代入圆锥的侧面积计算公式:S侧=12•2πr•l=π r l 有时还利用了圆的周长公式和扇形面积公式求解.
解题技巧提炼
根据扇形的弧长等于圆锥的底面周长求得半径,列出方程求解即可.
解题技巧提炼
此题主要考查了主要考查了圆锥的性质,要知道(1)圆锥的高,底面半径,母线构成直角三角形,(2)此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.解此类题目要根据所构成的直角三角形的勾股定理作为等量关系求解.
解题技巧提炼
本题考查圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.掌握圆锥的相关知识是解题的关键.
解题技巧提炼
本题考查了圆锥侧面展开图,扇形圆心角与母线和底面圆半径的关系,明确圆锥的底面圆的周长=扇形的弧长,通过列方程来解答本题的关键.
解题技巧提炼
把实际问题转化成数学问题来解决,明确求的是圆锥的哪个量,在套用公式即可.
解题技巧提炼
本题考查了平面展开﹣最短路径问题,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
解题技巧提炼
直接代入圆锥的侧面积计算公式:S侧=12•2πr•l=π r l 有时还利用了圆的周长公式和扇形面积公式求解.
解题技巧提炼
根据扇形的弧长等于圆锥的底面周长求得半径,列出方程求解即可.
解题技巧提炼
此题主要考查了主要考查了圆锥的性质,要知道(1)圆锥的高,底面半径,母线构成直角三角形,(2)此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.解此类题目要根据所构成的直角三角形的勾股定理作为等量关系求解.
解题技巧提炼
本题考查圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.掌握圆锥的相关知识是解题的关键.
解题技巧提炼
本题考查了圆锥侧面展开图,扇形圆心角与母线和底面圆半径的关系,明确圆锥的底面圆的周长=扇形的弧长,通过列方程来解答本题的关键.
解题技巧提炼
把实际问题转化成数学问题来解决,明确求的是圆锥的哪个量,在套用公式即可.
解题技巧提炼
本题考查了平面展开﹣最短路径问题,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
苏科版(2024)九年级上册2.7 弧长及扇形的面积课时训练: 这是一份苏科版(2024)九年级上册<a href="/sx/tb_c17319_t7/?tag_id=28" target="_blank">2.7 弧长及扇形的面积课时训练</a>,共52页。试卷主要包含了7 弧长及扇形面积等内容,欢迎下载使用。
初中苏科版(2024)2.4 圆周角精练: 这是一份初中苏科版(2024)<a href="/sx/tb_c17324_t7/?tag_id=28" target="_blank">2.4 圆周角精练</a>,共81页。试卷主要包含了4 圆 周 角,5,等内容,欢迎下载使用。
数学九年级上册2.3 确定圆的条件随堂练习题: 这是一份数学九年级上册<a href="/sx/tb_c17323_t7/?tag_id=28" target="_blank">2.3 确定圆的条件随堂练习题</a>,共49页。试卷主要包含了3 确定圆的条件,5°,,5.等内容,欢迎下载使用。













