









所属成套资源:人教版数学八年级下学期课件PPT+分层练习(原卷版+解析版)整套(含单元复习资料)
数学八年级下册19.2.1 正比例函数精品课件ppt
展开
这是一份数学八年级下册19.2.1 正比例函数精品课件ppt,文件包含人教版数学八年级下册19211《正比例函数的概念》同步课件pptx、人教版数学八年级下册19211《正比例函数的概念》分层练习原卷版docx、人教版数学八年级下册19211《正比例函数的概念》分层练习解析版docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
鸟类研究者在芬兰给一只燕鸥(候鸟)套上标志环;大约128天后,人们在2.56万千米外的澳大利亚发现了它.(1)这只百余克重的小鸟大约平均每天飞行多少千米?(2)这只燕鸥飞行一个半月(一个月按30天计算)的行程大约是多少千米?(3)这只燕鸥的行程y(单位:千米)与飞行时间x(单位:天)之间有什么关系?
下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式:
(1)某复印社按复印A4纸1张收0.4元计费,变量是复印纸张数x(张)与费用y(元).
(2)正方形ABCD的边长为6,P是边BC上的一点,变量是BP的长x与△ABP的面积S.
(3)圆的面积随半径变化而变化,变量是圆的面积S与该圆的半径r.
(4)冰的密度为1.0g/cm3,冰的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
(3)从地面到高空11千米处,高度每增加1千米,气温下降6℃,某地的地面气温是0 ℃,在11千米以下的空中,变量是空中某处离地面的气温t (℃) 和高度h(千米).
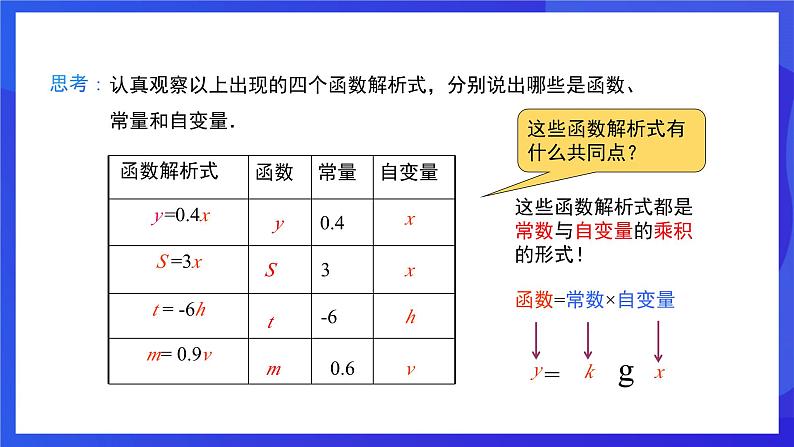
认真观察以上出现的四个函数解析式,分别说出哪些是函数、常量和自变量.
这些函数解析式有什么共同点?
这些函数解析式都是常数与自变量的乘积的形式!
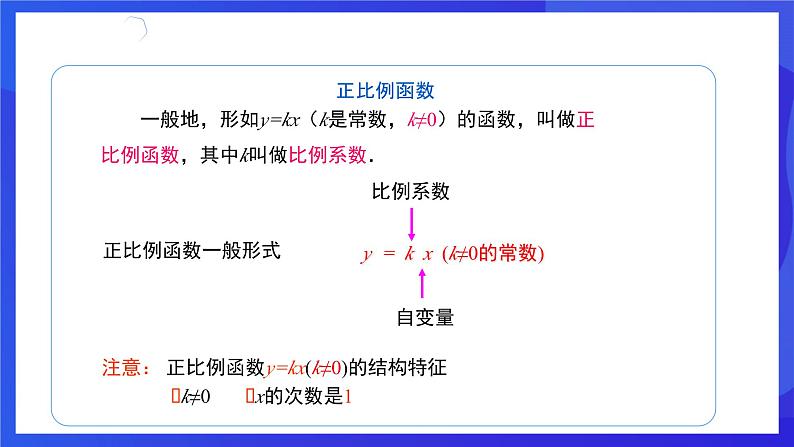
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
y = k x (k≠0的常数)
注意: 正比例函数y=kx(k≠0)的结构特征 ①k≠0 ②x的次数是1
判断下列函数解析式是否是正比例函数?如果是,指出其比例系数是多少?
一般情况下,正比例函数中自变量的取值范围是全体实数,但实际问题中,自变量的取值需要符合实际意义.
填空:(1)如果y=(k-1)x,是y关于x的正比例函数,则k满足____.(2)如果y=kxk-1,是y关于x的正比例函数,则k=__.(3)如果y=3x+k-4,是y关于x的正比例函数,则k=__.(4)如果y=(m-1)x|m|,是关于x的正比例函数,m= .
y与x之间的比例系数是 - 4
当x=-5时,y=20;当x=-2时,y=8;当x=0时,y=0;当x=3时,y=-12.
1.一般地,形如y=kx(k是常数,k≠0)的函数,叫做_____________, 其中k叫做比例系数.2.待定系数法求正比例函数的解析式的步骤:①设含有待定系数的函数的解析式为____________;②把已知条件代入__________;③解方程,求出待定系数k;④将求出的待定系数k代入所设解析式即可.
已知y1与x+1成正比例,y2与x-1成正比例,y=y1+y2,当x=2时,y=9;当x=3时,y=14.求y与x之间的函数解析式.解:设y1=k1(x+1),y2=k2(x-1),∴y=k1(x+1)+k2(x-1)=(k1+k2)x+k1-k2.将x=2,y=9,x=3,y=14代入上式中,解得k1=2,k2=3,∴y=5x-1.
已知 是正比例函数,求k的值.
已知y与x+2 成正比例,当x=4时,y=12,求当x=5时,y的值
∵y与x +2 成正比例
把x=4时,y=12代入①
当x=5时,y=14.
京沪高速铁路全长1318千米.2017年开始,京沪高速铁路开始使用我国研制的复兴号动车组列车,其平均速度为350km/h.考虑以下问题:(1) 乘复兴号高铁列车,从始发站北京南站到终点站上海虹桥站,约需多少小时(保留一位小数)?(2)京沪高铁的行程y(单位:千米)与时间t(单位:时)之间有何数量关系?
解:(1)1318÷350≈3.8(小时)
(2)y=350t(0≤t≤3.8)
(3)从北京南站出发2.5小时后,是否已经过了距始发站1000千米的南京南站?
(3)y=350×2.5=875(千米), 这时列车尚未到达距始发站1000千米的南京南站.
形式:y=kx(k≠0)
利用正比例函数解决简单的实际问题
4.下列函数中,表示y是x的正比例函数的是( )
B.y=x+2 C.y=x2 D.y=2x
6.填空:(1)若y=5x3m-2是正比例函数,则m=_____;(2)若y=(m-1)xm2是正比例函数,则m=_______.
5.已知y与x成正比例,当x等于3时,y等于-1.则当x=6时,y的值为 .
解:(1)设正比例函数解析式是 y=kx,
把 x =-8, y =4代入上式,得
∴所求的正比例函数解析式是 y= - ;
(2)当 x=4 时, y = -2.
9.若正比例函数的自变量x等于-8时,函数y的值等于4.
(1)求正比例函数的解析式;
(2)求当x=4时函数y的值.
10.已知某种小汽车的耗油量是每100km耗油15L.所使用的汽油为8元/ L .(1)写出汽车行驶途中所耗油费 y(元)与行程 x(km)之间的函数关系式,并指出y是x的什么函数;(2)计算该汽车行驶200 km所需油费是多少?
相关课件
这是一份数学八年级下册19.1.2 函数的图象一等奖课件ppt,文件包含人教版数学八年级下册19212《正比例函数的图象与性质》同步课件pptx、人教版数学八年级下册19212《正比例函数的图象与性质》分层练习原卷版docx、人教版数学八年级下册19212《正比例函数的图象与性质》分层练习解析版docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
这是一份人教版(2024)八年级下册19.1 变量与函数优秀课件ppt,文件包含人教版数学八年级下册19112《函数》同步课件pptx、人教版数学八年级下册19112《函数》分层练习原卷版docx、人教版数学八年级下册19112《函数》分层练习解析版docx等3份课件配套教学资源,其中PPT共28页, 欢迎下载使用。
这是一份数学八年级下册17.1 勾股定理完美版课件ppt,文件包含人教版数学八年级下册1711《勾股定理》同步课件pptx、人教版数学八年级下册1711《勾股定理》分层练习原卷版docx、人教版数学八年级下册1711《勾股定理》分层练习解析版docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。











