苏科版数学八上专题08 期末必练选择50道（18个考点）（2份，原卷版+解析版）

这是一份苏科版数学八上专题08 期末必练选择50道（18个考点）（2份，原卷版+解析版），文件包含苏科版数学八上专题08期末必练选择50道18个考点原卷版doc、苏科版数学八上专题08期末必练选择50道18个考点解析版doc等2份试卷配套教学资源，其中试卷共48页， 欢迎下载使用。
实战训练
一．平方根与立方根
1．若方程x2＝5的解分别为a、b，且a＞b，下列说法正确的是（ ）
A．5的平方根是aB．5的平方根是b
C．5的算术平方根是aD．5的算术平方根是b
试题分析：根据算术平方根、平方根的含义和求法，逐项判断即可．
答案详解：解：∵x2＝5的解分别为a、b，
∴5的平方根是a、b，
∴选项A不符合题意；
∵x2＝5的解分别为a、b，
∴5的平方根是a、b，
∴选项B不符合题意；
∵x2＝5的解分别为a、b，且a＞b，
∴5的算术平方根是a，
∴选项C符合题意；
∵x2＝5的解分别为a、b，且a＞b，
∴5的算术平方根是a，
∴选项D不符合题意．
所以选：C．
2．下列说法正确的是（ ）
A．4的算术平方根是2B．0.16的平方根是0.4
C．0没有立方根D．1的立方根是±1
试题分析：解：A：正数的算术平方根是正数；
B：正数的平方根有两个，并且互为相反数；
C：0有立方根；
D：正数的立方根只有1个正数．
答案详解：解：A：4的算术平方根是2，∴符合题意；
B：0.16的平方根是±0.4，∴不符合题意；
C：0有立方根，∴不符合题意；
D：1的立方根是1，∴不符合题意；
所以选：A．
二．非负数的和
3．已知实数x，y满足（x﹣3）2|z﹣5|＝0，则以x，y，z的值为边长的三角形的周长是（ ）
A．6B．12
C．14D．以上答案均不对
试题分析：根据绝对值、偶次方、算术平方根的非负性解决此题．
答案详解：解：∵（x﹣3）2≥0，0，|z﹣5|≥0，
∴当（x﹣3）2|z﹣5|＝0，则（x﹣3）2＝0，0，|z﹣5|＝0．
∴x＝3，y＝4，z＝5．
∴以x，y，z的值为边长的三角形的周长是3+4+5＝12．
所以选：B．
三．实数的理解与无理数的大小比较
4．在实数0、π、、、、3.1010010001中，无理数的个数有（ ）
A．1个B．2个C．3个D．4个
试题分析：无理数就是无限不循环小数，根据无理数的定义逐个判断即可．
答案详解：解：无理数有：π、，共2个，
所以选：B．
5．下列说法不正确的是（ ）
A．4的平方根是±2
B．正数、零和负数都有立方根
C．只有非负数才有平方根
D．﹣27的立方根是
试题分析：根据平方根与立方根的意义逐一判断即可．
答案详解：解：A．4的平方根是±2，故A不符合题意；
B．正数、零和负数都有立方根，故B不符合题意；
C．只有非负数才有平方根，故C不符合题意；
D．﹣27的立方根是﹣3，故D符合题意；
所以选：D．
6．下列四个数中，最大的实数是（ ）
A．B．0C．D．
试题分析：根据实数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，判断出四个数中，最小的数是哪个即可．
答案详解：解：∵0，
∴四个数中，最大的实数是．
所以选：C．
7．估算x值的大小正确的是（ ）
A．0＜x＜1B．1＜x＜2C．2＜x＜3D．3＜x＜4
试题分析：根据夹逼法进行无理数的估算即可得出答案．
答案详解：解：∵1＜3＜4，
∴12，
所以选：B．
四．新定义
8．对于任意的有理数a，b，如果满足，那么我们称这一对数a，b为“相随数对”，记为（a，b）．若（m，n）是“相随数对”，则3m+2[3m+（2n﹣1）]＝（ ）
A．﹣2B．﹣1C．2D．3
试题分析：根据（m，n）是“相随数对”得出9m+4n＝0，再将原式化成9m+4n﹣2，最后整体代入求值即可．
答案详解：解：∵（m，n）是“相随数对”，
∴，
∴，
即9m+4n＝0，
∴3m+2[3m+（2n﹣1）]
＝3m+2[3m+2n﹣1]
＝3m+6m+4n﹣2
＝9m+4n﹣2
＝0﹣2
＝﹣2，
所以选：A．
五．一次函数的图像
9．在同一平面直角坐标系中，关于下列函数：①y＝x+1；②y＝2x+1；③y＝2x﹣1；④y＝﹣2x+1的图象，说法不正确的是（ ）
A．②和③的图象相互平行
B．②的图象可由③的图象平移得到
C．①和④的图象关于y轴对称
D．③和④的图象关于x轴对称
试题分析：一次函数的比例系数相等则两直线平行，从而利用排除法确定答案；
答案详解：解：由题意得：y＝2x+1与y＝2x﹣1比例系数相等；y＝2x﹣1与y＝﹣2x+1的比例系数互为相反数，
所以②和③的图象相互平行，③和④的图象关于x轴对称，
故A、B、D正确，C错误，
所以选：C．
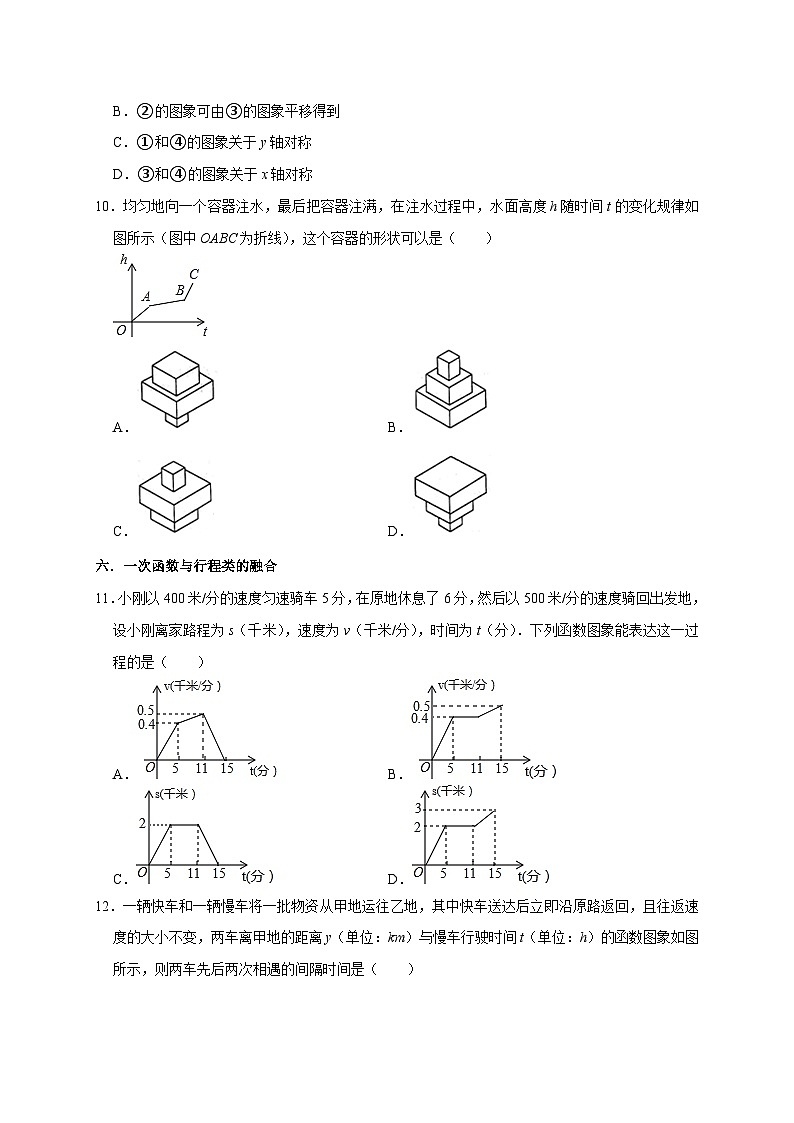
10．均匀地向一个容器注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为折线），这个容器的形状可以是（ ）
A．B．
C．D．
试题分析：根据每一段函数图象的倾斜程度，反映了水面上升速度的快慢，再观察容器的粗细，作出判断．
答案详解：解：注水量一定，从图中可以看出，OA上升较快，AB上升较慢，BC上升最快，
由此可知这个容器下面容积较大，中间容积最大，上面容积最小，
所以选：C．
六．一次函数与行程类的融合
11．小刚以400米/分的速度匀速骑车5分，在原地休息了6分，然后以500米/分的速度骑回出发地，设小刚离家路程为s（千米），速度为v（千米/分），时间为t（分）．下列函数图象能表达这一过程的是（ ）
A．B．
C．D．
试题分析：因为小刚以400米/分的速度匀速骑车5分，可求其行驶的路程对照各选除错误选项，“在原地休息”对应在图象上表示时间在增加，而距离不变，即这一线段与x轴平行，“回到原出发地”表示终点的纵坐标为0，综合分析选出正确答案．
答案详解：解：∵400×5＝2000（米）＝2（千米），
∴小刚以400米/分的速度匀速骑车5分行驶的路程为2千米
而选项A与B中纵轴表示速度，且速度为变量，这与事实不符，故排除选项A与B
又∵回到原出发地”表示终点的纵坐标为0，
∴排除选项D，
所以选：C．
12．一辆快车和一辆慢车将一批物资从甲地运往乙地，其中快车送达后立即沿原路返回，且往返速度的大小不变，两车离甲地的距离y（单位：km）与慢车行驶时间t（单位：h）的函数图象如图所示，则两车先后两次相遇的间隔时间是（ ）
A．hB．hC．hD．h
试题分析：根据题意和函数图象中的数据，可以分别求得快车和慢车的速度，然后即可求出第一次和第二次相遇的时间，再作差即可．
答案详解：解：由图象可得，
快车的速度为：（km/h），
慢车的速度为：km/h，
设两车第一次相遇的时间为mh，
则m（m﹣2），
解得m＝3，
两车第二次相遇的时间为nh，
n（n﹣4）＝a，
解得n，
即两车先后两次相遇的间隔时间是3（h），
所以选：D．
13．甲、乙两人沿同一条路从A地出发，去往100千米外的B地，甲、乙两人离A地的距离s（千米）与时间t（小时）之间的关系如图所示，以下说法正确的是（ ）
A．乙的速度是30km/h
B．甲出发1小时后两人第一次相遇
C．甲的速度是60km/h
D．甲乙同时到达B地
试题分析：根据题意和函数图象中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题．
答案详解：解：由图象可得，
乙的速度为：60÷3＝20（km/h），所以选项A错误，不符合题意；
甲的速度为：（100﹣40）÷（3﹣2）＝60（km/h），所以选项C正确，符合题意；
40÷60（小时），
即甲出发小时后两人第一次相遇，所以选项B错误，不符合题意；
乙出发3小时时走了60千米，此时甲到达B地，所以选项D错误，不符合题意；
所以选：C．
14．A、B两地相距20千米，甲、乙两人都从A地去B地，图中l1和l2分别表示甲、乙两人所走路程s（千米）与时间t（小时）之间的关系．下列说法错误的是（ ）
A．乙晚出发1小时B．乙出发3小时后追上甲
C．甲的速度是4千米/小时D．乙先到达B地
试题分析：根据函数图象中的数据，可以判断各个选项中的说法是否正确，本题得以解决．
答案详解：解：由图象可得，
乙晚出发1小时，所以选项A正确；
乙出发3﹣1＝2小时追上甲，所以选项B错误；
甲的速度是12÷3＝4（千米/小时），所以选项C正确；
乙先到达B地，所以选项D正确；
所以选：B．
七．一次函数与一元一次不等式
15．如图，一次函数y＝kx+b（k＞0）的图象过点（﹣1，0），则不等式k（x﹣2）+b＞0的解集是（ ）
A．x＞﹣2B．x＞﹣1C．x＞0D．x＞1
试题分析：先把（﹣1，0）代入y＝kx+b得b＝k，则k（x﹣2）+b＞0化为k（x﹣2）+k＞0，然后解关于x的不等式即可．
答案详解：解：把（﹣1，0）代入y＝kx+b得，﹣k+b＝0，
解得b＝k，
则k（x﹣2）+b＞0化为k（x﹣2）+k＞0，
即k（x﹣2+1）＞0，
而k＞0，
所以x﹣2+1＞0，
解得x＞1．
所以选：D．
方法二：
一次函数y＝kx+b（k＞0）的图象向右平移2个单位得y＝k（x﹣2）+b，
∵一次函数y＝kx+b（k＞0）的图象过点（﹣1，0），
∴一次函数y＝k（x﹣2）+b（k＞0）的图象过点（1，0），
由图象可知，当x＞1时，函数y＝k（x﹣2）+b＞0，
∴不等式k（x﹣2）+b＞0的解集是x＞1，
所以选：D．
16．如图，直线y1＝k1x+b和直线y2＝k2x+b分别与x轴交于A（﹣1，0）和B（3，0）两点，则不等式组的解集为（ ）
A．﹣1＜x＜3B．0＜x＜3C．﹣1＜x＜0D．x＞3或x＜﹣1
试题分析：观察函数图象，写出直线y1＝k1x+b在x轴上方和直线y2＝k2x+b在x轴上方所对应的自变量的范围即可．
答案详解：解：当x＝﹣1时，y1＝k1x+b＝0，则x＞﹣1时，y1＝k1x+b＞0，
当x＝3时，y2＝k2x+b＝0，则x＜3时，y2＝k2x+b＞0，
所以当﹣1＜x＜3时，k1x+b＞0，k2x+b＞0，
即不等式组的解集为﹣1＜x＜3．
所以选：A．
17．如图，已知直线y＝ax+2与直线y＝mx+b的交点的横坐标是﹣2．根据图象有下列四个结论：①a＞0；②b＜0；③方程ax+2＝mx+b的解是x＝﹣2；④不等式ax﹣b＞mx﹣2的解集是x＞﹣2．其中正确的结论个数是（ ）
A．1B．2C．3D．4
试题分析：根据一次函数的图象和性质可得a＞0；b＜0；直线y＝ax+2与直线y＝mx+b的交点的横坐标是﹣2，即方程ax+2＝mx+b的解为x＝﹣2；当x＞﹣2时，直线y＝ax+2在直线y＝mx+b的上方，即不等式ax﹣b＞mx﹣2的解集是x＞﹣2．
答案详解：解：由图象可知，a＞0，b＜0，故①②正确；
直线y＝ax+2与直线y＝mx+b的交点的横坐标是﹣2，即方程ax+2＝mx+b的解为x＝﹣2，故③正确；
当x＞﹣2时，直线y＝ax+2在直线y＝mx+b的上方，即不等式ax﹣b＞mx﹣2的解集是x＞﹣2，故④正确；
所以选：D．
18．如图，函数y＝2x和y＝ax+4的图象相交于点A（m，3），则不等式ax+4＞2x的解集是（ ）
A．xB．xC．x＞3D．x＜3
试题分析：首先利用待定系数法求出A点坐标，再以交点为分界，结合图象写出不等式ax+4＞2x解集即可．
答案详解：解：∵函数y＝2x过点A（m，3），
∴2m＝3，
解得：m，
∴A（，3），
∴不等式ax+4＞2x的解集为x．
所以选：B．
八．一次函数解析式的理解
19．关于函数y＝﹣2x+1，下列结论正确的是（ ）
A．图象经过点（﹣2，1）B．y随x的增大而增大
C．图象不经过第四象限D．图象与直线y＝﹣2x平行
试题分析：根据一次函数的性质对各选项进行逐一判断即可．
答案详解：解：A、当x＝﹣2，y＝﹣2x+1＝﹣2×（﹣2）+1＝5，则点（﹣2，1）不在函数y＝﹣2x+1图象上，故本选项错误；
B、由于k＝﹣2＜0，则y随x增大而减小，故本选项错误；
C、由于k＝﹣2＜0，则函数y＝﹣2x+1的图象必过第二、四象限，故本选项错误；
D、由于直线y＝﹣2x+1与直线y＝﹣2x+3的倾斜角相等且与y轴交于不同的点，所以它们相互平行，故本选项正确；
所以选：D．
九．巧用对称
20．如图，△PBC的面积为15cm2，PB为∠ABC的角平分线，作AP垂直BP于P，则△ABC的面积为（ ）
A．25cm2B．30cm2C．32.5cm2D．35cm2
试题分析：延长AP交BC于点Q，则由条件可知S△ABP＝S△BQP，S△APC＝S△PQC，则阴影部分面积为△ABC的一半，可得出答案．
答案详解：解：如图，延长AP交BC于点Q，
∵AP垂直∠ABC的平分线BP于P，
∴AP＝QP，
∴S△ABP＝S△BQP，S△APC＝S△PQC，
∴S△ABC＝2S阴影＝30cm2，
所以选：B．
21．如图，等腰△ABC中，AB＝AC＝3，BC＝5，边AC的垂直平分线分别交AC、BC于D、E，则△ABE的周长是（ ）
A．8B．9C．10D．11
试题分析：根据线段垂直平分线的性质可得AE＝CE，进而可得AE+BE＝BC＝5，进而可得答案．
答案详解：解：∵边AC的垂直平分线分别交AC、BC于点D、E，
∴AE＝CE，
∵BC＝5，
∴BE+CE＝5，
∵AB＝3，
∴△ABE的周长为3+5＝8．
所以选：A．
22．如图，△ABC中，∠ACB＝90°，AC＝4，BC＝3，将△ADE沿DE翻折，使点A与点B重合，则AE的长为（ ）
A．B．3C．D．
试题分析：在Rt△BCE中，由BE2＝CE2+BC2，得到（8﹣x）2＝x2+62，即可求解．
答案详解：解：设AE＝BE＝x，则CE＝4﹣x，
在Rt△BCE中，BE2＝CE2+BC2，
即x2＝（4﹣x）2+32，
解得x，
所以选：D．
十．读懂作图
23．如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画圆弧，分别交AB、AC于点D、E，再分别以点D、E为圆心，大于DE长为半径画圆弧，两弧交于点F，作射线AF交边BC于点G．若CG＝4，AB＝10，则△ABG的面积是（ ）
A．10B．20C．30D．40
试题分析：根据作图过程可得AG平分∠BAC，根据角平分线的性质即可解决问题．
答案详解：解：如图，过点G作GH⊥AB于点H，
由作图过程可知：AG平分∠BAC，
∵∠C＝90°，
∴GC⊥AC，
∴GH＝GC＝4，
∴△ABG的面积AB•GH10×4＝20．
所以选：B．
24．如图，在平行四边形ABCD中，AB＝4，BC＝5，以点C为圆心，适当长为半径画弧，交BC于点P，交CD于点Q，再分别以点P，Q为圆心，大于的长为半径画弧，两弧相交于点N，射线CN交BA的延长线于点E，则AE的长是（ ）
A．1B．2C．3D．4
试题分析：根据角平分线的定义和平行线的性质证得∠BCE＝∠E，由等腰三角形的判定得到BE＝BC，即可求得AE．
答案详解：解：由题意可知CE是∠BCD的平分线，
∴∠BCE＝∠DCE．
∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠DCE＝∠E，
∴∠BCE＝∠E，
∴BE＝BC＝5，
∵AB＝4，
∴AE＝BE﹣AB＝1，
所以选：A．
十一．格点图形的存在性
25．如图是由8个全等的小矩形组成的大正方形，线段AB的端点都在小矩形的顶点上，如果点P是某个小矩形的顶点，连接PA、PB，那么使△ABP为等腰直角三角形的点P的个数是（ ）
A．2个B．3个C．4个D．5个
试题分析：根据等腰直角三角形的判定即可得到结论．
答案详解：解：如图所示，使△ABP为等腰直角三角形的点P的个数是3，
所以选：B．
26．如图，设小方格的面积为1，则图中以格点为端点且长度为的线段有（ ）
A．2条B．3条C．4条D．5条
试题分析：是直角边长为2，3的直角三角形的斜边，据此画两条以格点为端点且长度为的线段．
答案详解：解：∵，
∴是直角边长为2，3的直角三角形的斜边，
如图所示，AB，CD，BE，DF的长都等于；
所以选：C．
27．如图3×3的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，则在此网格中与△ABC全等的格点三角形（不含△ABC）共有（ ）
A．5个B．6个C．7个D．8个
试题分析：根据全等三角形的判定定理画出符合的三角形，再得出选项即可．
答案详解：解：如图所示：与△ABC全等的三角形有△DEF、△HIJ、△GMN、△IEM、△HAF、△BDG、△CJN，共7个，
所以选：C．
28．在如图所示的3×3网格中，△ABC是格点三角形（即顶点恰好是网格线的交点），则与△ABC有一条公共边且全等（不含△ABC）的所有格点三角形的个数是（ ）
A．4个B．3个C．2个D．1个
试题分析：根据全等三角形的定义画出图形，即可判断．
答案详解：解：如图，观察图象可知满足条件的三角形有4个．
所以选：A．
十二．全等三角形的性质与判定
29．若△ABC≌△DEF，且∠A＝50°，∠B＝60°，则∠F的度数为（ ）
A．50°B．60°C．70°D．80°
试题分析：根据全等三角形的性质得出∠D＝∠A＝50°，∠E＝∠B＝60°，再根据三角形内角和定理求出∠F即可．
答案详解：解：∵△ABC≌△DEF，∠A＝50°，∠B＝60°，
∴∠D＝∠A＝50°，∠E＝∠B＝60°，
∴∠F＝180°﹣∠D﹣∠E＝180°﹣50°﹣60°＝70°，
所以选：C．
30．在△ABC中，AB＝AC，∠BAC＝45°，边AC、BC上的高BE、AD交点F．若BD，则AF的长为（ ）
A．1B．C．D．2
试题分析：根据等腰三角形的性质得出BC，进而利用全等三角形的判定和性质解答即可．
答案详解：解：∵AB＝AC，AD⊥BC，
∴BD＝DCBC，
∵BD，
∴BC＝2，
∵BE⊥AC，∠BAC＝45°，
∴BE＝AE，
∵∠C+∠EAF＝90°，∠C+∠EBC＝90°，
∴∠EAF＝∠EBC，
在△EAF和△EBC中，
，
∴△EAF≌△EBC（ASA），
∴AF＝BC＝2，
所以选：D．
31．如图，要测量河两岸相对的A、B两点的距离，可以在与AB垂直的河岸BF上取C、D两点，且使BC＝CD，从点D出发沿与河岸BF的垂直方向移动到点E，使点E与A，C在一条直线上，可得△ABC≌△EDC，这时测得DE的长就是AB的长．判定△ABC≌△EDC最直接的依据是（ ）
A．ASAB．HLC．SASD．SSS
试题分析：根据全等三角形的判定进行判断，注意看题目中提供了哪些证明全等的要素，要根据已知选择判断方法．
答案详解：解：因为证明在△ABC≌△EDC用到的条件是：CD＝BC，∠ABC＝∠EDC，∠ACB＝∠ECD，
所以用到的是两角及这两角的夹边对应相等即ASA这一方法．
所以选：A．
十三．等腰三角形的存在性--易漏三边关系
32．已知实数x，y满足，则以x，y的值为两边长的等腰三角形的周长是（ ）
A．20或16B．20
C．16D．以上答案均不对
试题分析：根据非负数的意义列出关于x、y的方程并求出x、y的值，再根据x是腰长和底边长两种情况讨论求解．
答案详解：解：根据题意得
，
解得，
（1）若4是腰长，则三角形的三边长为：4、4、8，
不能组成三角形；
（2）若4是底边长，则三角形的三边长为：4、8、8，
能组成三角形，周长为4+8+8＝20．
所以选：B．
33．已知实数x，y满足（x﹣5）20，则以x，y的值为两边长的等腰三角形的周长是（ ）
A．18B．21
C．18或21D．以上答案均不对
试题分析：先根据非负数的性质列式求出x、y的值，再分x的值是腰长与底边两种情况讨论求解．
答案详解：解：根据题意得：x﹣5＝0，y﹣8＝0，
解得x＝5，y＝8，
①5是腰长时，三角形的三边分别为5、5、8，能组成三角形，周长是5+5+8＝18；
②5是底边时，三角形的三边分别为5、8、8，能组成三角形，周长是5+8+8＝21．
所以等腰三角形的周长是18或21．
所以选：C．
34．若等腰三角形边长分别为6cm和3cm，则该等腰三角形的周长是（ ）
A．9cmB．12cmC．15cmD．12cm或15cm
试题分析：根据已知条件和三角形三边关系可知；等腰三角形的腰长不可能为3cm，只能为6cm，然后即可求得等腰三角形的周长．
答案详解：解：①6cm为腰，3cm为底，此时周长为6+6+3＝15cm；
②6cm为底，3cm为腰，则两边和等于第三边无法构成三角形，故舍去．
故其周长是15cm．
所以选：C．
十四．直角三角形斜边上的中线
35．如图，∠ABC＝∠ADC＝90°，∠BAD＝70°，点E是AC的中点．则∠EBD的度数为（ ）
A．20°B．35°C．40°D．55°
试题分析：根据已知条件得到点A，B，C，D在以E为圆心，AC为直径的同一个圆上，根据圆周角定理得到∠DEB＝140°，根据直角三角形的性质得到DE＝BEAC，根据等腰三角形的性质即可得到结论．
答案详解：解：连接DE，
∵∠ABC＝∠ADC＝90°，点E是AC的中点，
∴点A，B，C，D在以E为圆心，AC为直径的同一个圆上，
∵∠BAD＝70°，
∴∠DEB＝2∠BAD＝140°，
∵DE＝BEAC，
∴∠EBD＝∠EDB20°，
所以选：A．
36．如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，∠ABC＝45°，E是BD的中点，BD＝8，则△AEC的面积为（ ）
A．B．16C．8D．
试题分析：由直角三角形斜边上中线的性质可求E＝CE＝4，利用三角形外角的性质结合等腰三角形的性质可求解∠AEC＝90°，再利用三角形的面积公式计算可求解．
答案详解：解：∵∠BAD＝∠BCD＝90°，E是BD的中点，BD＝8，
∴AE＝CEBD＝4，
∴∠ABE＝∠BAE，∠CBE＝∠BCE，
∵∠AED＝∠ABE+∠BAE＝2∠ABE，∠CED＝∠CBE+∠BCE＝2∠CBE，
∴∠AEC＝2∠ABE+2∠CBE＝2∠ABC，
∵∠ABC＝45°，
∴∠AEC＝90°，
∴S△ACEAE•CE4÷4＝8．
所以选：C．
37．如图，BE和CD是△ABC的高，点G，F分别是DE，BC的中点，连接DF，FE，FG．下列结论正确的是（ ）
A．DE＝FGB．DF＝EF
C．DF⊥FED．DF平分线段BE
试题分析：根据直角三角形的性质得到DF＝EF，判断即可．
答案详解：解：∵BE和CD是△ABC的高，
∴∠BDC＝∠BEC＝90°，
∵点F是BC的中点，
∴DFBC，EFBC，
∴DF＝EF，故B选项说法正确，符合题意；
DE与FG的关系不确定，A选项说法错误，不符合题意；
DF与FE不一定垂直，C选项说法错误，不符合题意；
DF不一定平分线段BE，D选项说法错误，不符合题意；
所以选：B．
38．如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，BE是AC边上的中线，且BD＝CE，已知∠A＝38°，则∠BFC的度数是（ ）
A．111°B．110°C．109°D．108°
试题分析：连接DE，根据直角三角形斜边上的中线及余角的定义∠ADE＝∠A＝38°，∠ACD＝52°，可得∠DBE＝∠DEB＝19°，进而可求解∠BCD，∠CBE的度数，再利用三角形的内角和定理可求解．
答案详解：解：连接DE，
∵CD是AB边上的高，
∴∠ADC＝90°，
∵BE是AC边上的中线，∠A＝38°，
∴DE＝AE＝CE＝BD，∠ACD＝90°﹣38°＝52°，
∴∠ADE＝∠A＝38°，
∴∠DBE＝∠DEB＝19°，
∵∠ACB＝90°，
∴∠ABC＝90°﹣38°＝52°，∠BCD＝90°﹣52°＝38°，
∴∠CBE＝52°﹣19°＝33°，
∴∠BFC＝180°﹣33°﹣38°＝109°．
所以选：C．
十五．勾股定理的理解
39．已知直角三角形的两条边长分别是3和4，那么这个三角形的第三条边的长为（ ）
A．5B．25C．D．5或
试题分析：分两种情况：当3和4都是直角边时；当4是斜边长时；分别利用勾股定理计算出第三边长即可．
答案详解：解：当3和4都是直角边时，第三边长为：；
当4是斜边长时，第三边长为：．
所以选：D．
40．如图，正方形ABCD的面积为15，Rt△BCE的斜边CE的长为8，则BE的长为（ ）
A．17B．10C．6D．7
试题分析：由正方形的性质得BC2＝15，∠ABC＝90°，则∠EBC＝90°，再由勾股定理求出BE的长即可．
答案详解：解：∵正方形ABCD的面积为15，
∴BC2＝15，∠ABC＝90°，
∴∠EBC＝90°，
在Rt△BCE中，由勾股定理得：BE7，
所以选：D．
41．如图，在四边形ABCD中，连接AC、BD，已知∠ADB＝∠ACB＝90°，，则四边形ABCD的面积为（ ）
A．B．3C．D．4
试题分析：过C作CE⊥AD交AD的延长线于E，根据等腰直角三角形的性质得到AC＝BC，根据圆周角定理得到BAC＝∠BDC＝45°，求得CE＝DE＝1，根据勾股定理得到AE2，由三角形的面积公式即可得到结论．
答案详解：解：过C作CE⊥AD交AD的延长线于E，
∵∠ACB＝90°，∠CAB＝45°，
∴△ACB是等腰直角三角形，
∴AC＝BC，
∵∠ADB＝∠ACB＝90°，
∴A，B，C，D四点共圆，
∴∠BAC＝∠BDC＝45°，
∵∠ADB＝90°，
∴∠EDB＝90°，
∴∠EDC＝45°，
∴△CED是等腰直角三角形，
∵CD，
∴CE＝DE＝1，
∵AE2，
∴AD＝1，
∴四边形ABCD的面积＝S△ACD+S△ACBAD•CEAC•BC1×13，
所以选：B．
十六．勾股定理的逆定理
42．下列各组数据中，不能作为直角三角形三边长度的是（ ）
A．9，12，15B．7，24，25C．，2，D．1，，
试题分析：先分别求出两小边的平方和和最长边的平方，再根据勾股定理的逆定理逐个判断即可．
答案详解：解：A．∵92+122＝81+144＝225，152＝225，
∴92+122＝152，
∴以9，12，15为边能组成直角三角形，故本选项不符合题意；
B．∵72+242＝49+576＝625，252＝625，
∴72+242＝252，
∴以7，24，25为边能组成直角三角形，故本选项不符合题意；
C．∵（）2+22＝3+4＝7，（）2＝5，
∴（）2+22≠（）2，
∴以，2，为边不能组成直角三角形，故本选项符合题意；
D．∵12+（）2＝1+2＝3，（）2＝3，
∴12+（）2＝（）2，
∴以1，，为边能组成直角三角形，故本选项不符合题意；
所以选：C．
43．下列四组线段中，可以构成直角三角形的是（ ）
A．4，5，6B．2，3，4C．，，D．，，4
试题分析：先分别求出两小边的平方和最长边的平方，再看看是否相等即可．
答案详解：解：A．∵42+52＝16+25＝41，62＝36，
∴42+52≠62，
∴以4，5，6为边不能组成直角三角形，故本选项不符合题意；
B．∵22+32＝4+9＝13，42＝16，
∴22+32≠42，
∴以2，3，4为边不能组成直角三角形，故本选项不符合题意；
C．∵（）2+（）2＝2+3＝5，（）2＝5，
∴（）2+（）2＝（）2，
∴以，，为边能组成直角三角形，故本选项符合题意；
D．∵（）2+（）2＝7+3＝10，42＝16，
∴（）2+（）2≠42，
∴以，，4为边不能组成直角三角形，故本选项不符合题意；
所以选：C．
44．满足下列条件的△ABC不是直角三角形的是（ ）
A．∠A：∠B：∠C＝3：4：5B．BC＝1，AC＝2，AB
C．BC：AC：AB＝3：4：5D．BC＝1，AC＝2，AB
试题分析：利用三角形内角和定理和勾股定理逆定理进行计算可得答案．
答案详解：解：A．∠A：∠B：∠C＝3：4：5，
∴设∠A＝3x，∠B＝4x，∠C＝5x，
∴∠A+∠B+∠C＝3x+4x+5x＝180°，
∴x＝15°，
∴∠C＝5x＝5×15°＝75°，
∴△ABC不是直角三角形，符合题意．
B．∵BC＝1，AC＝2，AB，12+22＝（）2，
∴BC2+AC2＝AB2，
满足勾股定理逆定理，故△ABC是直角三角形，不符合题意．
C．∵BC：AC：AB＝3：4：5，
∴设BC＝3k，AC＝4k，AB＝5k，
∴（3k）2+（4k）2＝（5k）2，
∴BC2+AC2＝AB2，
∴满足勾股定理逆定理，
∴△ABC是直角三角形，不符合题意．
D．∵BC＝1，AC＝2，AB，12+（）2＝22，
∴BC2+AB2＝AC2，
满足勾股定理逆定理，故△ABC是直角三角形，不符合题意．
所以选：A．
十七．勾股定理的应用
45．如图，长为16cm的橡皮筋放置在数轴上，固定两端A和B，然后把中点C向上拉升6cm至D点，则橡皮筋被拉长了（ ）
A．4cmB．5cmC．6cmD．7cm
试题分析：据勾股定理，可求出AD、BD的长，则AD+BD﹣AB即为橡皮筋拉长的距离．
答案详解：解：Rt△ACD中，ACAB＝8cm，CD＝6cm；
根据勾股定理，得：AD10（cm）；
∴AD+BD﹣AB＝2AD﹣AB＝20﹣16＝4（cm）；
故橡皮筋被拉长了4cm．
所以选：A．
46．如图，将风筝放至高30m，牵引线与水平面夹角约为45°的高空中，则牵引线AB的长度所在范围最有可能是（ ）
A．36m至38mB．38m至40mC．40m至42mD．42m至44m
试题分析：过B作BC⊥水平面于C，证△ABC是等腰直角三角形，得AC＝BC＝30m，再由勾股定理求出AB的长，即可得出结论．
答案详解：解：如图，过B作BC⊥水平面于C，
∵∠BAC＝45°，
∴△ABC是等腰直角三角形，
∴AC＝BC＝30m，
∴AB3042.42（m），
所以选：D．
十八．动点类
47．如图，在△ABC中，∠ABC＝90°，BC＝4，AB＝8，P为AC边上的一个动点，D为PB上的一个动点，连接AD，当∠CBP＝∠BAD时，线段CD的最小值是（ ）
A．B．2C．D．
试题分析：根据∠CBP＝∠BAD，得∠ABD+∠BAD＝90°，则∠ADB＝90°，取AB的中点E，连接DE，CE，利用勾股定理求出OC的长，从而得出答案．
答案详解：解：∵∠ABC＝90°，
∴∠ABP+∠CBP＝90°，
∵∠CBP＝∠BAD，
∴∠ABD+∠BAD＝90°，
∴∠ADB＝90°，
取AB的中点E，连接DE，CE，
∴DEAB＝4，
∴OCOB＝4，
∵CD≥CE﹣DE，
∴CD的最小值为44，
所以选：D．
48．如图，边长为5的等边三角形ABC中，M是高CH所在直线上的一个动点，连接MB，将线段BM绕点B逆时针旋转60°得到BN，连接HN．则在点M运动过程中，线段HN长度的最小值是（ ）
A．B．1C．2D．
试题分析：取CB的中点G，连接MG，根据等边三角形的性质可得BH＝BG，再求出∠HBN＝∠MBG，根据旋转的性质可得MB＝NB，然后利用“边角边”证明△MBG≌△NBH，再根据全等三角形对应边相等可得HN＝MG，然后根据垂线段最短可得MG⊥CH时最短，再根据∠BCH＝30°求解即可．
答案详解：解：如图，取BC的中点G，连接MG，
∵旋转角为60°，
∴∠MBH+∠HBN＝60°，
又∵∠MBH+∠MBC＝∠ABC＝60°，
∴∠HBN＝∠GBM，
∵CH是等边△ABC的对称轴，
∴HBAB，
∴HB＝BG，
又∵MB旋转到BN，
∴BM＝BN，
在△MBG和△NBH中，
，
∴△MBG≌△NBH（SAS），
∴MG＝NH，
根据垂线段最短，MG⊥CH时，MG最短，即HN最短，
此时∵∠BCH60°＝30°，CGAB5，
∴MGCG，
∴HN，
所以选：A．
49．如图，在平面直角坐标系中，点P坐标为（﹣2，3），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于（ ）
A．﹣4和﹣3之间B．3和4之间C．﹣5和﹣4之间D．4和5之间
试题分析：先根据勾股定理求出OP的长，由于OP＝OA，故估算出OA的长，再根据点A在x轴的负半轴上即可得出结论．
答案详解：解：∵点P坐标为（﹣2，3），
∴OP，
∵点A、P均在以点O为圆心，以OP为半径的圆上，
∴OA＝OP，
∵9＜13＜16，
∴34．
∵点A在x轴的负半轴上，
∴点A的横坐标介于﹣4和﹣3之间．
所以选：A．
50．如图，在平面直角坐标系中，设一质点M自P0（1，0）处向上运动1个单位至P1（1，1），然后向左运动2个单位至P2处，再向下运动3个单位至P3处，再向右运动4个单位至P4处，再向上运动5个单位至P5处，…，如此继续运动下去，则P2022的坐标为（ ）
A．（1011，1011）B．（﹣1011，1011）
C．（504，﹣505）D．（505，﹣504）
试题分析：根据第一象限中点的特征，探究规律，利用规律解决问题．
答案详解：解：由题意P1（1，1），P5（3，3），P9（5，5），•••P2021（1011，1011），
P2022的纵坐标与P2021的纵坐标相同，
∴P2022（﹣1011，1011），
所以选：B．