人教版数学七下重难点培优训练专题5.6 平行线中的综合（压轴题）（2份，原卷版+解析版）

这是一份人教版数学七下重难点培优训练专题5.6 平行线中的综合（压轴题）（2份，原卷版+解析版），文件包含人教版数学七下重难点培优训练专题56平行线中的综合压轴题原卷版doc、人教版数学七下重难点培优训练专题56平行线中的综合压轴题解析版doc等2份试卷配套教学资源，其中试卷共65页， 欢迎下载使用。

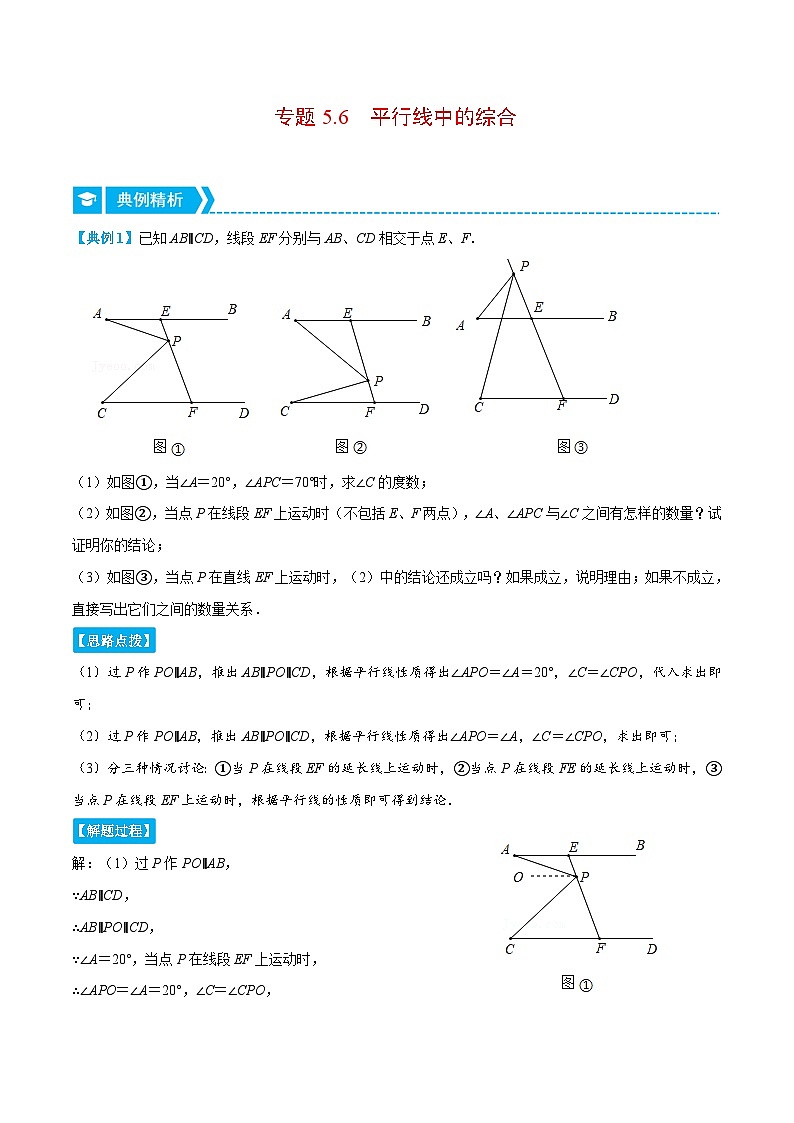
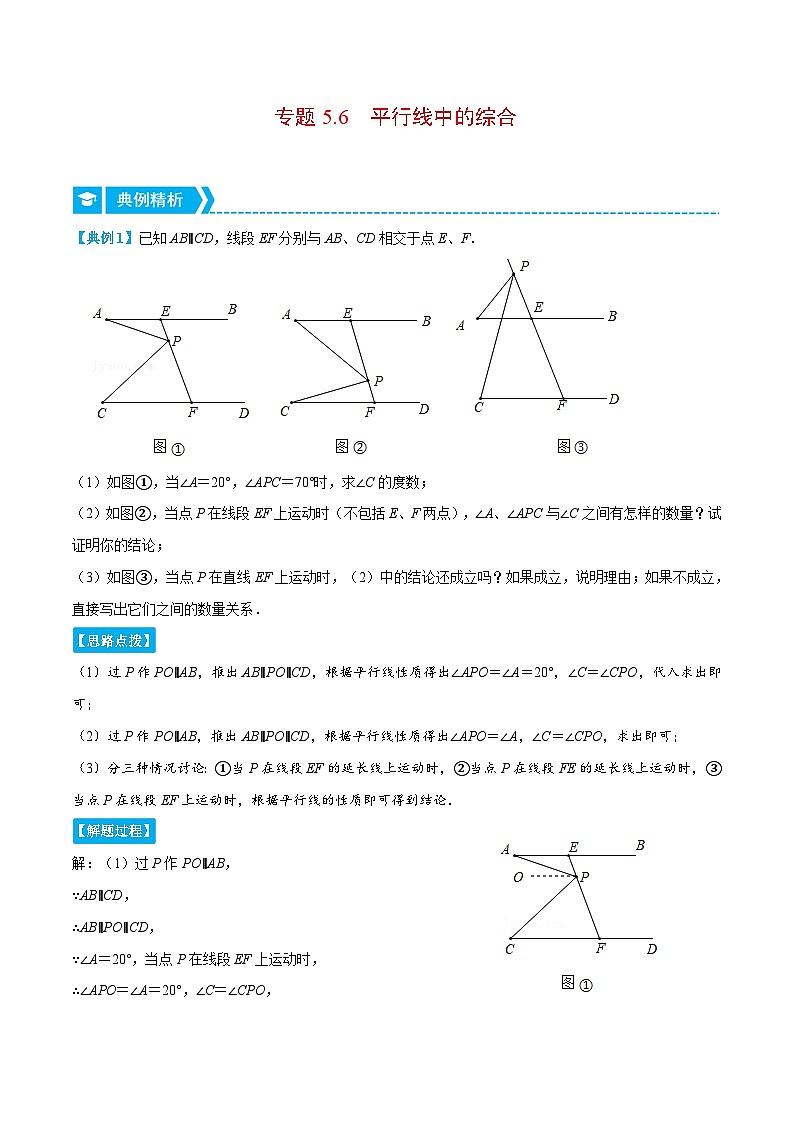
【典例1】已知AB∥CD，线段EF分别与AB、CD相交于点E、F．
（1）如图①，当∠A＝20°，∠APC＝70°时，求∠C的度数；
（2）如图②，当点P在线段EF上运动时（不包括E、F两点），∠A、∠APC与∠C之间有怎样的数量？试证明你的结论；
（3）如图③，当点P在直线EF上运动时，（2）中的结论还成立吗？如果成立，说明理由；如果不成立，直接写出它们之间的数量关系．
【思路点拨】
（1）过P作PO∥AB，推出AB∥PO∥CD，根据平行线性质得出∠APO＝∠A＝20°，∠C＝∠CPO，代入求出即可；
（2）过P作PO∥AB，推出AB∥PO∥CD，根据平行线性质得出∠APO＝∠A，∠C＝∠CPO，求出即可；
（3）分三种情况讨论：①当P在线段EF的延长线上运动时，②当点P在线段FE的延长线上运动时，③当点P在线段EF上运动时，根据平行线的性质即可得到结论．
【解题过程】
解：（1）过P作PO∥AB，
∵AB∥CD，
∴AB∥PO∥CD，
∵∠A＝20°，当点P在线段EF上运动时，
∴∠APO＝∠A＝20°，∠C＝∠CPO，
∵∠APC＝70°，
∴∠C＝∠CPO＝∠APC﹣∠APO＝70°﹣20°＝50°；
（2）∠A+∠C＝∠APC，
证明：过P作PO∥AB，
∵AB∥CD，
∴AB∥PO∥CD，
∴∠APO＝∠A，∠C＝∠CPO，
∴∠APC＝∠APO+∠CPO＝∠A+∠C；
（3）解：①当P在线段EF的延长线上运动时，不成立，关系式是：∠A﹣∠C＝∠APC，
理由是：过P作PO∥AB，
∵AB∥CD，
∴AB∥PO∥CD，
∴∠APO＝∠A，∠C＝∠CPO，
∴∠A﹣∠C＝∠APO﹣∠CPO＝∠APC，
即∠A﹣∠C＝∠APC；
②当点P在线段FE的延长线上运动时，新的相等关系为∠C＝∠APC+∠A．
理由：设AB与CP相交于Q，则∠PQB＝∠APC+∠A．
∵AB∥CD，
∴∠C＝∠PQB，
∴∠C＝∠APC+∠A．
③当点P在线段EF上运动时，成立，关系式为∠A+∠C＝∠APC，
证明：过P作PO∥AB，
∵AB∥CD，
∴AB∥PO∥CD，
∴∠APO＝∠A，∠C＝∠CPO，
∴∠APC＝∠APO+∠CPO＝∠A+∠C；
综上所述，当点P在直线EF上运动时，（2）中的结论不一定成立．
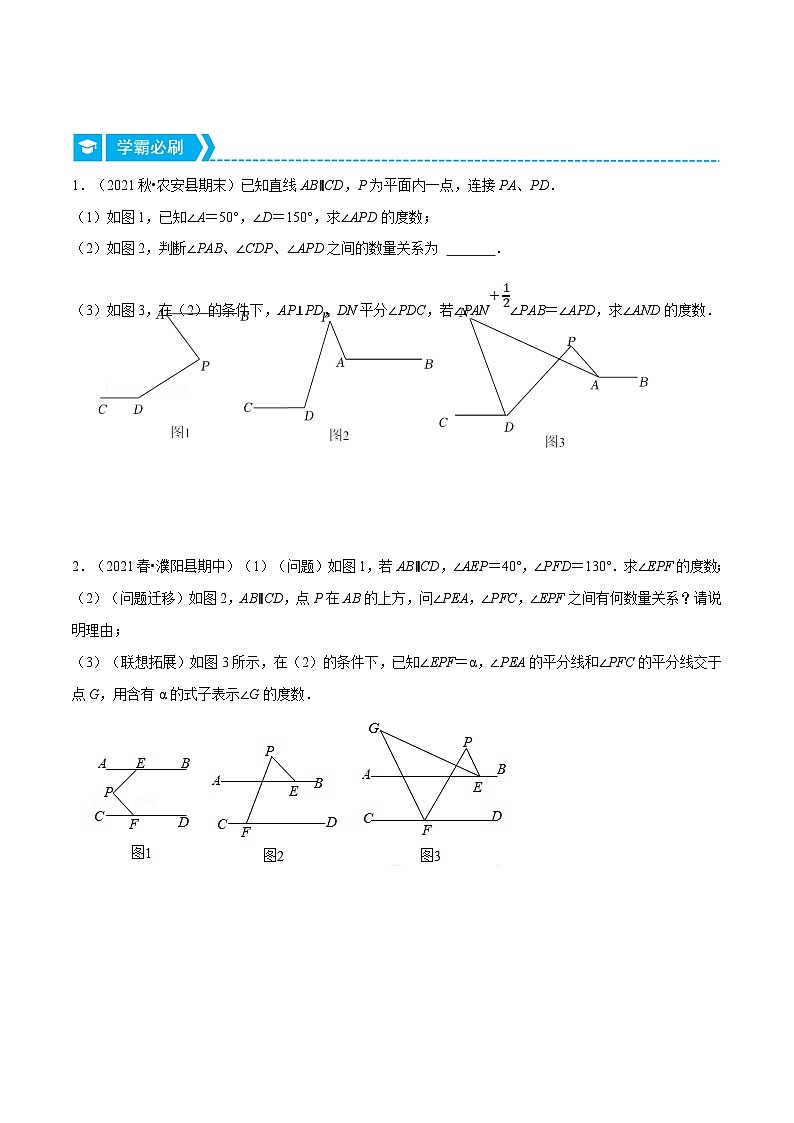
1．（2021秋•农安县期末）已知直线AB∥CD，P为平面内一点，连接PA、PD．
（1）如图1，已知∠A＝50°，∠D＝150°，求∠APD的度数；
（2）如图2，判断∠PAB、∠CDP、∠APD之间的数量关系为 ．
（3）如图3，在（2）的条件下，AP⊥PD，DN平分∠PDC，若∠PAN∠PAB＝∠APD，求∠AND的度数．
2．（2021春•濮阳县期中）（1）（问题）如图1，若AB∥CD，∠AEP＝40°，∠PFD＝130°．求∠EPF的度数；
（2）（问题迁移）如图2，AB∥CD，点P在AB的上方，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；
（3）（联想拓展）如图3所示，在（2）的条件下，已知∠EPF＝α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．
3．（2021春•鼓楼区校级期中）如图1，已知BE平分∠ABD，DE平分∠BDC，且∠EBD+∠EDB＝90°．
（1）求证：AB∥CD；
（2）如图2．射线BF、DF交于点F，且∠BFD＝30°，当∠ABE＝3∠ABF时，试探决∠CDF与∠CDE的比值，并说明理由；
（3）若点H是直线CD上一动点（不与点D重合），BI平分∠HBD．请直接写出∠EBI与∠BHD的数量关系．
4．（2021春•丹东期末）已知：AB∥CD．
（1）探究∠B、∠BED、∠D之间的数量关系，并说明理由；
（2）利用上述中的结论，
①如图2，已知AB∥CD，试探究∠E、∠G、∠B、∠F、∠D之间的数量关系，并说明理由；
②如图3，已知AB∥CD，请直接写出∠B、∠D、∠E1、∠E2……∠En、∠F1、∠F2…∠Fn+1之间的数量关系．
5．（2021秋•太仓市期末）如图所示，已知直线AB∥直线CD，直线EF分别交直线AB、CD于点A，C．且∠BAC＝60°，现将射线AB绕点A以每秒2°的转速逆时计旋转得到射线AM．同时射线CE绕点C以每秒3°的转速顺时针旋转得到射线CN，当射线CN旋转至与射线CA重合时，则射线CN、射线AM均停止转动，设旋转时间为t（秒）．
（1）在旋转过程中，若射线AM与射线CN相交，设交点为P．
①当t＝20（秒）时，则∠CPA＝ °；
②若∠CPA＝70°，求此时t的值；
（2）在旋转过程中，是否存在AM∥CN？若存在，求出此时t的值；若不存在，请说明理由．
6．（2021秋•皇姑区期末）已知：直线AB∥CD，直线AD与直线BC交于点E，∠AEC＝110°．
（1）如图①，BF平分∠ABE交AD于F，DG平分∠CDE交BC于G，求∠AFB+∠CGD的度数；
（2）如图②，∠ABC＝30°，在∠BAE的平分线上取一点P，连接PC，当∠PCD∠PCB时，直接写出∠APC的度数．
7．（2021秋•南岗区校级期末）已知：直线AB∥CD，一块三角板EFH，其中∠EFH＝90°，∠EHF＝60°．
（1）如图1，三角板EFH的顶点H落在直线CD上，并使EH与直线AB相交于点G，若∠2＝2∠1，求∠1的度数；
（2）如图2，当三角板EFH的顶点F落在直线AB上，且顶点H仍在直线CD上时，EF与直线CD相交于点M，试确定∠E、∠AFE、∠MHE的数量关系；
（3）如图3，当三角板EFH的顶点F落在直线AB上，顶点H在AB、CD之间，而顶点E恰好落在直线CD上时得△EFH，在线段EH上取点P，连接FP并延长交直线CD于点T，在线段EF上取点K，连接PK并延长交∠CEH的角平分线于点Q，若∠Q﹣∠HFT＝15°，且∠EFT＝∠ETF，求证：PQ∥FH．
8．（2020春•河东区期末）已知：点A、C、B不在同一条直线上，AD∥BE
（1）如图①，当∠A＝58°，∠B＝118°时，求∠C的度数；
（2）如图②，AQ、BQ分别为∠DAC、∠EBC的平分线所在直线，试探究∠C与∠AQB的数量关系；
（3）如图③，在（2）的前提下，且有AC∥QB，QP⊥PB，直接写出∠DAC：∠ACB：∠CBE的值．
9．（2021春•新洲区期末）如图1，点E在直线AB、DC之间，且∠DEB+∠ABE﹣∠CDE＝180°．
（1）求证：AB∥DC；
（2）若点F是直线BA上的一点，且∠BEF＝∠BFE，EG平分∠DEB交直线AB于点G，若∠D＝20°，求∠FEG的度数；
（3）如图3，点N是直线AB、DC外一点，且满足∠CDM∠CDE，∠ABN∠ABE，ND与BE交于点M．已知∠CDM＝α（0°＜α＜12°），且BN∥DE，则∠NMB的度数为 （请直接写出答案，用含α的式子表示）．
10．（2021春•宜兴市月考）如图①，已知PQ∥MN，且∠BAM＝2∠BAN．
（1）填空：∠PBA＝ °；
（2）如图（1）所示，射线AM绕点A开始顺时针旋转至AN便立即按原速度回转至AM位置，射线BP绕点B开始顺时针旋转至BQ便立即按原速度回转至BP位置．若AM转动的速度是每秒2度，BP转动的速度是每秒1度，若射线BP先转动30秒，射线AM才开始转动，在射线BP到达BQ之前，射线AM转动几秒，两射线互相平行？
（3）如图（2），若两射线分别绕点A，B顺时针方向同时转动，速度同题（2），在射线AM到达AN之前，若两射线交于点C，过C作∠ACD交PQ于点D，且∠ACD＝120°，则在转动过程中，请探究∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请说明理由．
11．如图，直线PQ∥MN，点A、B分别是PQ、MN上的两点，点C是PQ、MN之间（不在直线PQ、MN上）的一个动点，且∠ACB＝90°，BD平分∠CBM交PQ于点D．
（1）如图1，若∠PDB＝120°，求∠NBC的度数；
（2）如图1，在（1）问的条件下，求∠QAC的度数；
（3）延长AC交直线MN于点G，如图2，GH平分∠AGB交DB于H，设∠CBM＝2x°，∠AGB＝2y°，请探究∠GHB的度数是否与x、y的取值有关？并说明理由．
12．（2021春•重庆期中）已知：AB∥CD，E、G是AB上的点，F、H是CD上的点，∠1＝∠2．
（1）如图1，求证：EF∥GH；
（2）如图2，过F点作FM⊥GH交GH延长线于点M，作∠BEF、∠DFM的角平分线交于点N，EN交GH于点P，求证：∠N＝45°；
（3）如图3，在（2）的条件下，作∠AGH的角平分线交CD于点Q，若3∠FEN＝4∠HFM，直接写出的值．
13．（2021春•莱山区期末）我区正在打造某河流夜间景观带，计划在河两岸设置两座可以旋转的射灯．如图1，灯A射线从AM开始顺时针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射．若灯A转动的速度是2度/秒，灯B转动的速度是1度/秒，假定河两岸是平行的，即PQ∥MN，且∠BAM＝2∠BAN．
（1）∠BAN＝ 度．
（2）灯A射线从AM开始顺时针旋转至AN需要 秒；
（3）若灯B射线BD（交MN于点D）先转动30秒，灯A射线AC（交PQ于点C）才开始转动．设AC转动时间为t秒，当AC到达AN之前时，如图2所示．
①∠PBD＝ 度，∠MAC＝ 度（用含有t的代数式表示）；
②求当AC转动几秒时，两灯的光束射线AC∥BD？
（4）在BD到达BQ之前，是否还存在某一时刻，使两灯的光束射线AC∥BD？若存在，直接写出转动时间，若不存在，请说明理由．
14．（2021春•硚口区期末）已知直线EF分别交直线AB、CD于点G、H，∠1+∠2＝180°．
（1）如图1，求证：AB∥CD；
（2）如图2，M、N分别为直线AB、CD上的点，P、Q为直线AB、CD之间不同的两点，∠PMQ＝2∠BMQ，∠PNQ＝2∠DNQ，∠MQN＝30°．
①求证：PM⊥PN；
②如图3，∠EGB的平分线GL与∠MPN的邻补角∠MPT的平分线PL交于点L，∠PNH的平分线NK交EF于点K．若∠EKN+∠GLP＝170°，直接写出∠PNH﹣∠EHD的大小．
15．（2021春•汉阳区期中）如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，F，EM平分∠AEF交CD于点M，且∠FEM＝∠FME．
（1）直线AB与直线CD的位置关系是 ；
（2）如图2，点G是射线FD上一动点（不与点F重合），EH平分∠FEG交CD于点H，过点H作HN⊥EM于点N，设∠EHN＝α，∠EGF＝β．
①当点G在运动过程中，若β＝56°，求α的度数；
②当点G在运动过程中，α和β之间有怎样的数量关系？请写出你的猜想，并加以证明．
16．（2021春•枣阳市期末）（1）特例发现：如图1，AB∥CD，CE平分∠ACD，AE平分∠BAC．请观察猜想∠AEC的度数并说明理由；
（2）类比探究：如图2，点M是AE上一点，当∠E＝90°保持不变，移动直角顶点E，使CE平分∠MCD．∠BAE与∠MCD存在怎样的数量关系？并说明理由；
（3）拓展应用：如图3，P为线段AC上一定点，点Q为直线CD上一动点，点Q不与点C重合．∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．
17．（2021秋•丰泽区期末）已知AB∥CD，点M在直线AB上，点N、Q在直线CD上，点P在直线AB、CD之间，连接PM、PN、PQ，PQ平分∠MPN，如图①．
（1）若∠PMA＝α、∠PQC＝β，求∠NPQ的度数（用含α，β的式子表示）；
（2）过点Q作QE∥PN交PM的延长线于点E，过E作EF平分∠PEQ交PQ于点F，如图②，请你判断EF与PQ的位置关系，并说明理由；
（3）在（2）的条件下，连接EN，如图③，若∠NEF∠PMA，求证：NE平分∠PNQ．
18．（2021秋•南岗区校级期中）已知：如图，AB∥CD．
（1）如图1，求证：∠EAB+∠AED+∠EDC＝360°；
（2）如图2，若AF平分∠EAB，DF平分∠EDC，设∠AFD＝α，求∠AED的度数；（用含α的式子表示）（3）如图3，在（2）的条件下，过A作AH∥ED交DC于点H，AD平分∠EAH，∠DAG：∠FDC＝1：3，
AF延长线交CD于点G，求∠BAH的度数．
19．（2020秋•仁寿县期末）如图①．已知AM∥CN，点B为平面内一点，AB⊥BC于点B，过点B作BD⊥AM于点D，设∠BCN＝α．
（1）若α＝30°，求∠ABD的度数；
（2）如图②，若点E、F在DM上，连接BE、BF、CF，使得BE平分∠ABD、BF平分∠DBC，求∠EBF的度数；
（3）如图③，在（2）问的条件下，若CF平分∠BCH，且∠BFC＝3∠BCN，求∠EBC的度数．
20．（2021秋•揭东区期末）已知：如图所示，直线MN∥GH，另一直线交GH于A，交MN于B，且∠MBA＝80°，点C为直线GH上一动点，点D为直线MN上一动点，且∠GCD＝50°．
（1）如图1，当点C在点A右边且点D在点B左边时，∠DBA的平分线交∠DCA的平分线于点P，求∠BPC的度数；
（2）如图2，当点C在点A右边且点D在点B右边时，∠DBA的平分线交∠DCA的平分线于点P，求∠BPC的度数；
（3）当点C在点A左边且点D在点B左边时，∠DBA的平分线交∠DCA的平分线所在直线交于点P，请直接写出∠BPC的度数，不说明理由．