2023-2024学年山东省烟台市莱州市九年级(上)期中数学试卷(解析版)

这是一份2023-2024学年山东省烟台市莱州市九年级(上)期中数学试卷(解析版)，共18页。试卷主要包含了故选B等内容，欢迎下载使用。
注意事项：
1．本试卷分试题卷和答题卡，试题卷共6页，共3道大题，24道小题，满分120分．考试时间为120分钟．
2．答题前，请将自己的班级、姓名、座号填写在相应的位置上．
一、选择题（本题共12个小题，下列每小题均给出标号为A、B、C、D的四个备选答案，其中只有一个是正确的）．
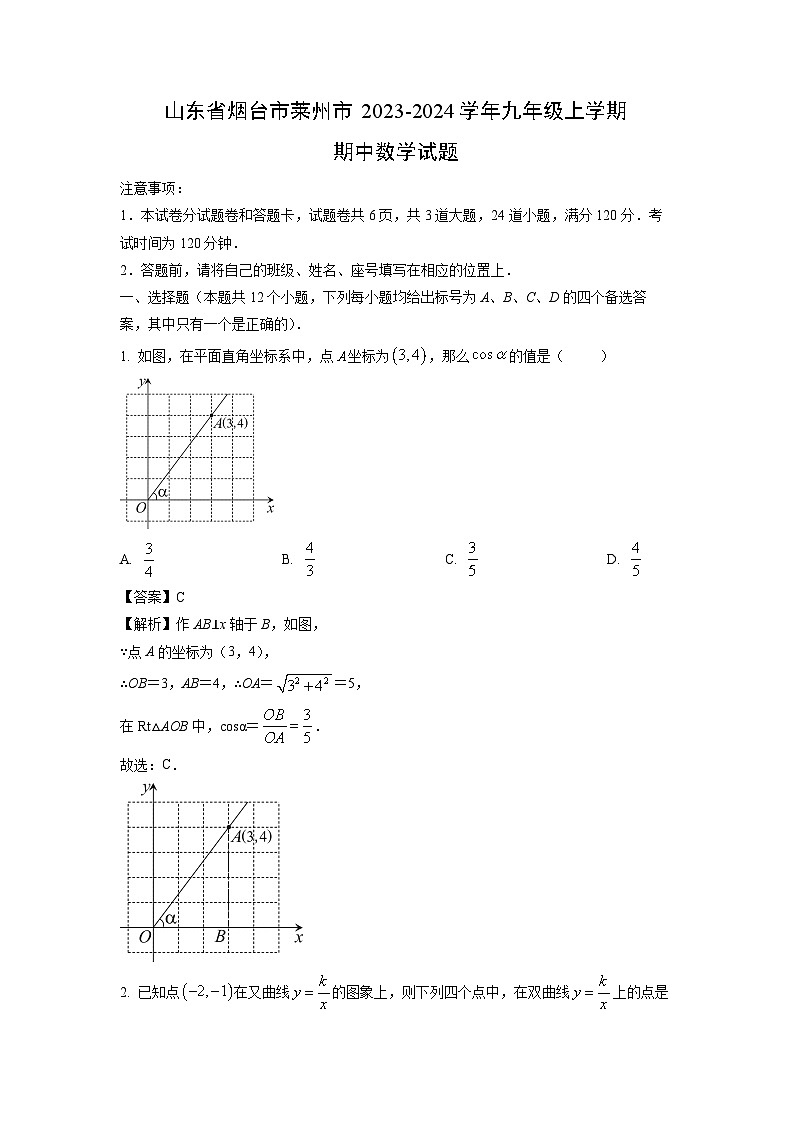
1. 如图，在平面直角坐标系中，点坐标为，那么的值是（ ）
A. B. C. D.
【答案】C
【解析】作AB⊥x轴于B，如图，
∵点A的坐标为（3，4），
∴OB＝3，AB＝4，∴OA＝＝5，
在Rt△AOB中，csα＝．
故选：C．
2. 已知点在又曲线的图象上，则下列四个点中，在双曲线上的点是（ ）
A. B. C. D.
【答案】D
【解析】∵已知点在又曲线的图象上，
∴，
∴即双曲线上的点的横纵坐标之积为2，
∵，，，，
故选：D．
3. 已知某抛物线上有三点，分别为，，，当时，y随x的增大而增大，当时，y随x的增大而减小，则，，由小到大的顺序排列的是（ ）
A. B.
C. D.
【答案】A
【解析】由题意可知，抛物线开口向上，对称轴为直线，
关于直线的对称点为，
∵，当时，y随x的增大而增大，
∴，故选：A．
4. 已知反比例函数，下列说法错误的是（ ）
A. 在每个象限内，y的值随x的值增大而增大
B. 是轴对称图形，也是中心对称图形
C. 过原点的直线与交于点，则该直线与一定还交于点
D. 图象分别位于第二、四象限内
【答案】C
【解析】A、，，在每个象限内，y的值随x的值增大而增大，故A选项正确；
B、反比例函数图象，是轴对称图形，也是中心对称图形，故B选项正确；
C、过原点的直线与交于点，则该直线与一定还交于点，故C选项错误；
D、图象分别位于第二、四象限内，故D选项正确
故选：C．
5. 若用我们数学课本上采用的科学计算器计算，按键顺序正确的是（ ）
A.
B.
C.
D.
【答案】C
【解析】若用我们数学课本上采用的科学计算器计算sin42°16′，按键顺序正确的是
．
故选：C．
6. 反比例函数与二次函数在同一平面直角坐标系中的大致图像是（ ）
A. B.
C. D.
【答案】D
【解析】当k＞0时，二次函数图像开口向下，顶点在y轴的正半轴；反比例函数图像在第一、三象限；
当k＜0时，二次函数的图像开口向上，顶点在y轴的负半轴；反比例函数图像在第二、四象限，故选项D正确；
故选：D．
7. 二次函数的图象如图所示，则m的值是( )
A. －8B. 8C. ±8D. 6
【答案】B
【解析】∵由图可知，抛物线与x轴只有一个交点，
∴对应的一元二次方程的△=m2﹣4×2×8=0，解得m=±8，
∵对称轴为直线，∴m＞0．
∴m的值为8．故选B．
8. 一配电房示意图如图所示，它是一个轴对称图形，已知米，房檐到地面的高度为4米，屋顶斜坡的坡角为a，则房顶A离地面的高度是（ ）
A. 米B. 米
C. 米D. 米
【答案】D
【解析】如图，过点作于，
∵图形是一个轴对称图形，米，
米，
中，，
∴（米），
∴房顶离地面的高度为：米，
故选：D．
9. 如图，在中，，．点P是边上一动点（不与C，B重合），过点P作交于点．设，的长为，的面积为，则与x，S与满足的函数关系分别为（ ）

A. 一次函数关系，二次函数关系B. 反比例函数关系，二次函数关系
C. 一次函数关系，反比例函数关系D. 反比例函数关系，一次函数关系
【答案】A
【解析】∵在中，，，
∴，
∵，∴，
∵，∴，
在中，，，
∴，，
∴与x，S与满足的函数关系分别为一次函数关系，二次函数关系，
故选A．
10. 如图是二次函数的图象，其对称轴为，且与轴交于点．下列结论：①；②；③；④抛物线与轴另一交点坐标为；⑤．其中正确的结论有（ ）
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】抛物线开口向下，
，
对称轴在轴右侧，
，
抛物线与轴交于正半轴，
，
，故①错误，
，，
，故②正确，
抛物线与轴有两个交点，
，故③正确，
抛物线与轴的一个交点为，对称轴为，
抛物线与轴的另一个交点为，故④正确，
抛物线与轴的一个交点为，，
，，故⑤错误．
故选：C．
二、填空题（本题共8个小题）
11. 若函数是反比例函数，则______．
【答案】
【解析】∵函数为反比例函数，
∴且．解得．故答案是：．
12. 二次函数的图象如图所示，与x轴交点坐标为，与y轴交点坐标为，对称轴为，则其解析式为______．
【答案】
【解析】∵二次函数的图象与x轴交点坐标为，对称轴为，
∴与x轴另一个交点坐标为，
设二次函数的解析式为，
把代入得，，
解得，
∴，
∴其解析式为，
故答案为：．
13. 如图所示，网格中的每个小正方形的边长都是1，的顶点都在格点处，则的正弦值为______．
【答案】
【解析】如图，
在中
．
故答案为：
14. 如图，直线与反比例函数交于点B，与x轴和y轴分别交于点A和点D，于点C，若点D是线段的中点，，，则k的值为______．
【答案】
【解析】在中，，，
∴，
∵于点C，
∴，
∴，
∴，
∵点D是线段的中点，
∴，，
∴，
∵点B在反比例函数的图象上，
∴，
故答案为：．
15. 如图，小明一家自驾到风景区C游玩，到达A地后，导航显示车辆应沿北偏西方向行驶一段距离至B地，再沿北偏东方向行驶千米到达风景区C，小明发现风景区C在A地的北偏东方向，那么A，B两地的距离为______千米．
【答案】4
【解析】如图所示，过点B作于D，
由题意得，，
∴，
∵，
∴，
∴，，
∴，千米，
∴（千米），
答：A，B两地的距离为4千米．
故答案为：4．
16. 加工爆米花时，爆开且不糊的颗粒的百分比称为“可食用率”．在特定条件下，可食用率与加工时间（单位：）满足函数表达式，则最佳加工时间为________．
【答案】3.75
【解析】∵的对称轴为（min），
故：最佳加工时间为3.75min，
故答案为：3.75．
三、解答题（本大题共8个小题，要写出必要的解答过程或推理步骤）
17. 计算：2tan45°﹣﹣2sin260°．
解：原式＝2×1﹣﹣2×（）2＋＝2﹣2﹣＝0；
18. 如图，在中，是边上的高，，，．
（1）求的值；
（2）求的面积．
解：（1）∵在中，，，
∴．
∴，
∴；
（2）∵，
∴．
∵，，
∴，
∴，
∴．
19. 工匠制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料煅烧到，然后停止煅烧进行锻造操作，经过时，材料温度降为．煅烧时温度与时间成一次函数关系；锻造时，温度与时间成反比例函数关系（如图）．已知该材料初始温度是．

（1）分别求出材料煅烧和锻造时y与x的函数关系式；
（2）根据工艺要求，当材料温度低于时，需停止操作，那么锻造的操作时间有多长？
解：（1）设材料停止煅烧后y与x的函数关系式为，
∵
∴，
∴，
∴，
把代入得，
，
∴，
∴，
∴材料停止煅烧后y与x的函数关系式为；
设材料煅烧时y与x的函数关系式为，
∵，
∴，
∴，
∴材料煅烧时y与x的函数关系式为；
（2）把代入，
∴，
∴，
．
答：锻造操作时间为．
20. 如图，A（4，3）是反比例函数y=在第一象限图象上一点，连接OA，过A作AB∥x轴，截取AB=OA（B在A右侧），连接OB，交反比例函数y=的图象于点P．
（1）求反比例函数y=的表达式；
（2）求点B的坐标；
（3）求△OAP的面积．
解：（1）将点A（4，3）代入y=，得：k=12，则反比例函数解析式为y=；
（2）如图，过点A作AC⊥x轴于点C，
则OC=4、AC=3，
∴OA==5，
∵AB∥x轴，且AB=OA=5，
∴点B的坐标为（9，3）；
（3）∵点B坐标为（9，3），
∴OB所在直线解析式为y=x，
由可得点P坐标为（6，2），（负值舍去），
过点P作PD⊥x轴，延长DP交AB于点E，
则点E坐标为（6，3），
∴AE=2、PE=1、PD=2，
则△OAP的面积=×（2+6）×3﹣×6×2﹣×2×1=5．
21. 无人机在实际生活中应用广泛．如图所示，小明利用无人机测量大楼的高度，无人机在空中处，测得楼楼顶处的俯角为，测得楼楼顶处的俯角为．已知楼和楼之间的距离为米，楼的高度为10米，从楼的处测得楼的处的仰角为（点在同一平面内，参考数据：）．

（1）填空：______________度；
（2）求楼的高度；
（3）求此时无人机距离地面的高度（结果精确到1米）．
解：（1）
，
过点作于点，
则 ，
，
故答案为：75
（2）过点作于点，则米，米，
在中，，
米．
答：楼的高度为110米．
（3）过点作于点，交于点，

在中，
（米）
答：此时无人机距离地面的高度约为183米．
22. 如图，在足够大的空地上有一段长为40米的旧墙，某人利用旧墙和木栏围成一个矩形菜园，其中，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．设矩形中，边为米，面积为平方米．
（1）求与之间的函数关系式，并写出自变量的取值范围；
（2）求矩形菜园面积的最大值．
解：（1）设矩形中，边为米，面积为平方米，则米，
由矩形面积公式可得：；
，
∴；
∴与之间的函数关系式为；
（2），
∵，对称轴为，
∴时，随的增大而增大，
∴时，；
答：当为40米时，矩形菜园面积的最大值为1200平方米．
23. 一次足球训练中，小明从球门正前方的A处射门，球射向球门的路线呈抛物线．当球飞行的水平距离为时，球达到最高点，此时球离地面．已知球门高为2.44m，现以O为原点建立如图所示直角坐标系．

（1）求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）．
（2）对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点O正上方2.25m处？
解：（1）由题意得：抛物线的顶点坐标为，
设抛物线解析式为，
把点代入，得，
解得，
∴抛物线的函数表达式为，
当时，，
∴球不能射进球门；
（2）设小明带球向正后方移动米，则移动后的抛物线为，
把点代入得，解得（舍去），，
∴当时他应该带球向正后方移动1米射门．
24. 如图，已知抛物线经过两点．

（1）求抛物线的解析式和顶点坐标；
（2）当时，直接写出y的取值范围；
（3）点P为抛物线上一点，若，求出此时点P的坐标．
解：（1）将代入，
得：，解得：，
∴抛物线的解析式为：，
∴顶点坐标为；
（2）由（1）可知抛物线的对称轴为：，开口向下，
∴当时，y随x的增大而增大，当时，y随x的增大而减小，
∴当时，y有最大值，为4．
当时，，
∴；
（3）设，则的高为，
∵，
∴．
∵，
∴，
解得：，
当时，即，
此时方程无解；
当时，即
解得：或，
∴或．