




所属成套资源:浙教版数学八上期末专题训练专题 (2份,原卷版+解析版)
- 浙教版数学八上期末专题训练专题18 一次函数的定义压轴题五种模型全攻略(2份,原卷版+解析版) 试卷 1 次下载
- 浙教版数学八上期末专题训练专题19 一次函数的图像和性质压轴题十种模型全攻略(2份,原卷版+解析版) 试卷 2 次下载
- 浙教版数学八上期末专题训练专题21 用一次函数解决实际问题压轴题五种模型全攻略(2份,原卷版+解析版) 试卷 2 次下载
- 浙教版数学八上期末专题训练专题22 高频题型专题:一次函数的图象信息题压轴题三种模型全攻略(2份,原卷版+解析版) 试卷 3 次下载
- 浙教版数学八上期末专题训练专题23 专项题型专训:一次函数与面积问题压轴题四种模型全攻略(2份,原卷版+解析版) 试卷 2 次下载
浙教版数学八上期末专题训练专题20 易错易混集训:一次函数压轴题三种易错模型全攻略(2份,原卷版+解析版)
展开
这是一份浙教版数学八上期末专题训练专题20 易错易混集训:一次函数压轴题三种易错模型全攻略(2份,原卷版+解析版),文件包含浙教版数学八上期末专题训练专题20易错易混集训一次函数压轴题三种易错模型全攻略原卷版doc、浙教版数学八上期末专题训练专题20易错易混集训一次函数压轴题三种易错模型全攻略解析版doc等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
易错点一 忽略一次函数中“k≠0”或正比例函数是特殊的一次函数致错
易错点二 忽略自变量的取值范围致错
易错点三 一次函数图象与坐标轴的交点位置不明确时忘记分类讨论
典型例题
易错点一 忽略一次函数中“k≠0”或正比例函数是特殊的一次函数致错
例题:(2022·安徽·淮北一中八年级阶段练习)当为何值时,函数是一次函数?求该一次函数的表达式.
【答案】时是一次函数,
【分析】根据一次函数的定义得到,求出m,舍去不符合的结果,即可得到函数解析式.
【详解】解:由题意得:.解得或,
当吋,,
所以应舍去,
所以,
这个一次函数表达式为.
【点睛】此题考查了一次函数的定义,求一次函数的解析式,正确掌握一次函数的定义是解题的关键.
【变式训练】
一、填空题
1.(2022·广东·深圳市西乡中学八年级期中)已知函数是关于的一次函数,则的值是_______.
【答案】
【分析】函数是一次函数,则,,由此即可求解.
【详解】解:根据题意得,,,
∴,,
∴,
故答案是:.
【点睛】本题主要考查一次函数的定义,理解一次函数的定义,系数不为零,未知数的次数为是解题的关键.
2.(2022·山东烟台·七年级期末)若是关于x的一次函数,则m等于_________.
【答案】
【分析】根据一次函数的定义,形如y=kx+b(k,b为常数,k≠0),进行计算即可.
【详解】解:由题意得:|m|=1且m−1≠0,
∴m=±1且m≠1,
∴m=−1,
故答案为:−1.
【点睛】本题考查了一次函数的定义,熟练掌握一次函数的定义是解题的关键.
3.(2021·安徽省六安皋城中学八年级期中)若y=(m+2)x+m2-4是关于x的一次函数且过原点,则常数m的值为______.
【答案】2
【分析】根据一次函数图象经过原点可得m2-4=0,再根据一次函数定义可得m+2≠0,再解即可.
【详解】解:∵一次函数y=(m+2)x+m2-4过原点,
∴m2-4=0,且m+2≠0,
解得:m=2,
故答案为:2.
【点睛】此题主要考查了一次函数定义,关键是掌握一次函数y=kx+b(k≠0,k、b为常数),当b=0时,是正比例函数,图象经过原点.
4.(2022·山东东营·七年级期末)若函数是表示一次函数,则等于_______.
【答案】0
【分析】根据一次函数的定义解答.
【详解】解:由题意得,
解得k=0,
故答案为:0.
【点睛】此题考查了一次函数的定义:形如的函数是一次函数,熟记定义是解题的关键.
5.(2021·宁夏·银川市第三中学八年级期中)已知函数是一次函数,则m的值是______.
【答案】0
【分析】根据一次函数的定义可列方程:,,求解即可得出m的值.
【详解】根据一次函数定义可知:
且,
解得:.
故答案为:0.
【点睛】本题考查了一次函数的定义,形如,其中,x的次数是1,常数b可以为任意实数.
6.(2021·广东·深圳市南山外国语学校八年级期中)若y=(m﹣1)x|m|+m+1是关于x的一次函数,则m等于 ___.
【答案】-1
【分析】根据一次函数的概念:形如y=kx+b(k≠0,k、b为常数)的函数,可知m-1≠0,,进而求解即可.
【详解】解:由题意得:
m-1≠0,,
解得:;
故答案为-1.
【点睛】本题主要考查一次函数的概念,熟练掌握一次函数的概念是解题的关键.
7.(2022·四川·成都嘉祥外国语学校八年级期中)若函数y=(m-3)+m-1是一次函数,则m的值为_______.
【答案】1
【分析】根据一次函数的定义可得且,求解即可.
【详解】解:∵函数y=(m-3)+m-1是一次函数,
∴且,
解得,
故答案为:1.
【点睛】本题考查一次函数的定义,掌握一次函数的定义是解题的关键.
二、解答题
8.(2022·全国·八年级专题练习)已知函数y=(m﹣1)x+1﹣
(1)当m为何值时,这个函数是关于x的一次函数?
(2)当m为何值时,这个函数是关于x的正比例函数?
【答案】(1)m≠1
(2)m=﹣1
【分析】(1)根据一次函数的形式,y=kx+b(k≠0),即可进行解答;
(2)根据正比例函数的形式,y=kx(k≠0),即可进行解答.
(1)
解:∵函数y=(m﹣1)x+1﹣是关于x的一次函数,
∴m﹣1≠0,
解得m≠1,
即当m为不等于1的值时,这个函数是关于x的一次函数;
(2)
∵函数y=(m﹣1)x+1﹣是关于x的正比例函数,
∴m﹣1≠0且1﹣=0,
解得m=﹣1,
即当m为﹣1时,这个函数是关于x的正比例函数.
【点睛】本题主要考查了正比例函数和一次函数的一般形式,熟练掌握相关内容是解题的关键.
9.(2021·四川省乐至实验中学八年级阶段练习)已知关于的函数
(1)和取何值时,该函数是关于的一次函数?
(2)和取何值时,该函数是关于的正比例函数?
【答案】(1),为任意实数;(2),
【分析】(1)如果函数关系式是关于自变量的一次式,则称为一次函数,用字母表示为y=kx+b,其中k≠0,且k、b为常数;根据一次函数的定义及表示形式完成即可;
(2)若一次函数表达式中b=0,即y=kx,其中k≠0,则称此函数为正比例函数,根据正比例函数的解析式完成即可.
【详解】(1)由题意知:,则m=±1
当m=-1时,m+1=0
∴m=1
n可为任意实数
即当m=1,n为任意实数时,函数为一次函数.
(2)由(1)知,m=1
但n-3=0,所以n=3
即当m=1,n=3时,函数是正比例函数.
【点睛】本题考查了一次函数与正比例函数的定义及解析式,关键是掌握两种函数的定义,另外要清楚一次函数与正比例函数是一般与特殊的关系.
10.(2022·全国·八年级课时练习)已知.
(1)满足什么条件时,是一次函数?
(2)满足什么条件时,是正比例函数?
【答案】(1);(2).
【分析】(1)形如是一次函数,根据一次函数的定义解题;
(2)形如是正比例函数,根据正比例函数的定义解题.
【详解】(1):当时为一次函数,
解得.
(2):当时为正比例函数,
解得.
【点睛】本题考查一次函数、正比例函数的定义,其中涉及绝对值等知识,是重要考点,难度较易,掌握相关知识是解题关键.
11.(2022·广东·深圳市龙岗区宏扬学校八年级期中)已知函数.
(1)当为何值时,是的一次函数,并写出关系式;
(2)当为何值时,是的正比例函数,并写出关系式.
【答案】(1)当m=-2,n为任意实数时,是的一次函数,关系式为;(2)当m=-2,n=-4时,是的正比例函数,关系式为
【分析】(1)根据一次函数的定义即可求出结论;
(2)根据正比例函数的定义即可求出结论.
【详解】解:(1)由题意可得,n可以取任意实数
解得:m=-2
∴
∴当m=-2,n为任意实数时,是的一次函数,关系式为;
(2)由题意可得,
解得:
∴
∴当m=-2,n=-4时,是的正比例函数,关系式为.
【点睛】此题考查的是根据一次函数和正比例函数的定义,求参数问题,掌握一次函数和正比例函数的定义是解题关键.
12.(2022·全国·八年级)已知函数.
(1)当m为何值时,y是x的一次函数?
(2)若函数是一次函数,则x为何值时,y的值为3?
【答案】(1)时,是一次函数;(2)时,y的值为3.
【分析】(1)根据一次函数的定义即可列出关于m的方程和不等式,从而求出m的值;
(2)将y=3代入一次函数中,即可求出x的值.
【详解】(1)由是一次函数得,
解得.
故当时,是一次函数.
(2)由(1)可知.
当时,,解得.
故当时,y的值为3.
【点睛】此题考查的是根据一次函数求函数中参数的值以及根据函数值求自变量的值,掌握一次函数的定义是解决此题的关键.
易错点二 忽略自变量的取值范围致错
例题:(2022·北京·前门外国语学校八年级阶段练习)已知蜡烛被燃烧的长度与燃烧时间成正比例,长为的蜡烛,点燃6分钟后,蜡烛变短了,设蜡烛点燃x分钟后的长度为,
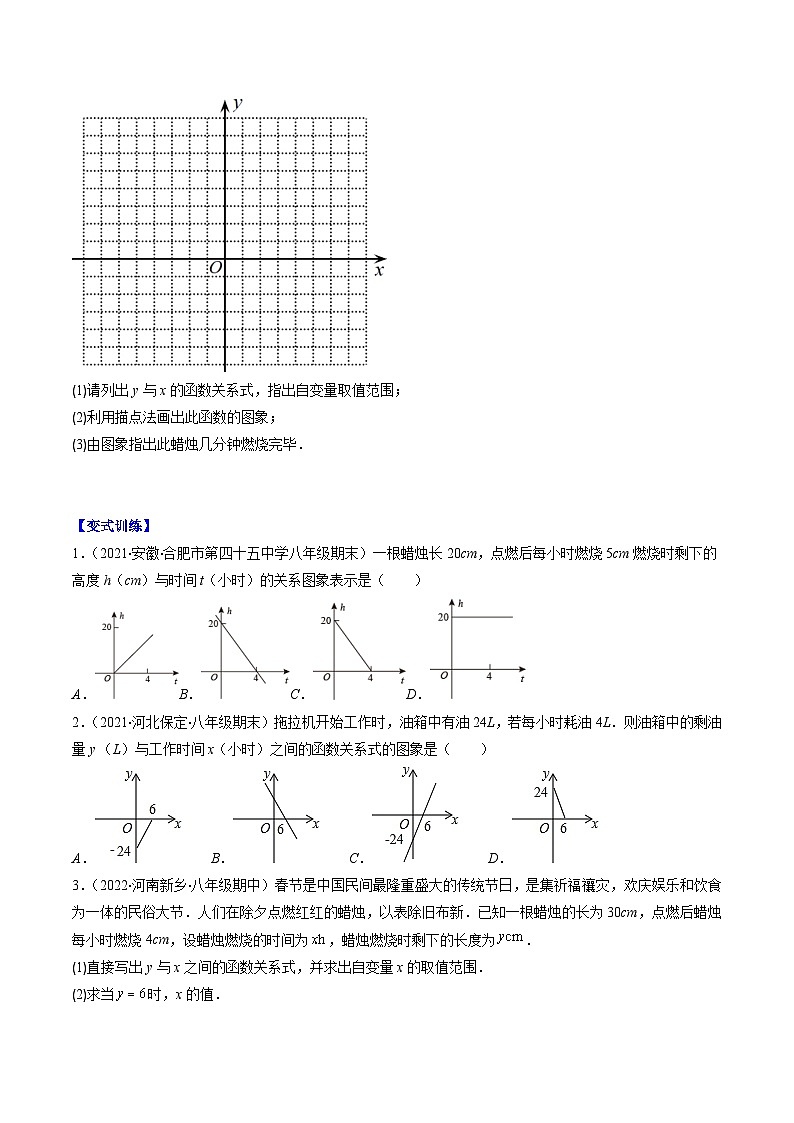
(1)请列出y与x的函数关系式,指出自变量取值范围;
(2)利用描点法画出此函数的图象;
(3)由图象指出此蜡烛几分钟燃烧完毕.
【答案】(1)y与x之间的关系式是y=24-0.6x,0≤x≤40;
(2)见解析;
(3)此蜡烛40分钟燃烧完毕.
【分析】(1)根据蜡烛点燃后的长度=原长度-每分钟燃烧的长度×时间,建立函数关系式用待定系数法求解,并求出自变量的取值范围;
(2)用描点法画出函数图像;
(3)从图像直接可以得出结论.
(1)
由题意可得,
y=24-x=24-0.6x,
∴y与x之间的关系式是y=24-0.6x,
令y=0,则24-0.6x=0,
解得:x=40,
∴自变量x的取值范围是:0≤x≤40;
(2)
列表为:
图象是一条线段.描点并连线为:
(3)
由图像可以看出:此蜡烛40分钟燃烧完毕.
【点睛】此题考查了根据题意中的等量关系建立函数关系式;能够根据函数解析式求得对应的x的值,特别注意自变量的取值范围.
【变式训练】
1.(2021·安徽·合肥市第四十五中学八年级期末)一根蜡烛长20cm,点燃后每小时燃烧5cm燃烧时剩下的高度h(cm)与时间t(小时)的关系图象表示是( )
A.B.C.D.
【答案】C
【分析】先根据题意求出与的函数关系式,再根据一次函数的图象特征即可得.
【详解】由题意得:,
,
,
解得,
即与的关系式为,是一次函数图象的一部分,且随的增大而减小,
观察四个选项可知,只有选项C符合,
故选:C.
【点睛】本题考查了一次函数的图象,依据题意,正确求出一次函数的解析式是解题关键.
2.(2021·河北保定·八年级期末)拖拉机开始工作时,油箱中有油24L,若每小时耗油4L.则油箱中的剩油量y (L)与工作时间x(小时)之间的函数关系式的图象是( )
A.B.C.D.
【答案】D
【分析】根据剩余油量=邮箱里原有的油量-消耗的油量就可以表示出y与x之间的函数关系式.
【详解】解:由题意,得
y=24-4x(0≤x≤6).
∴k=-4<0,
∴函数是降函数,函数图象是线段.
当x=0时,y=24,当y=0时,x=6.
∴函数图象是经过(0,24)和(6,0)的线段.
故选D.
【点睛】本题考查了运用剩余油量=邮箱里原有的油量-消耗的油量的关系的运用,一次函数的解析式的运用,解答时求出函数的解析式是关键.
3.(2022·河南新乡·八年级期中)春节是中国民间最隆重盛大的传统节日,是集祈福禳灾,欢庆娱乐和饮食为一体的民俗大节.人们在除夕点燃红红的蜡烛,以表除旧布新.已知一根蜡烛的长为30cm,点燃后蜡烛每小时燃烧4cm,设蜡烛燃烧的时间为,蜡烛燃烧时剩下的长度为.
(1)直接写出y与x之间的函数关系式,并求出自变量x的取值范围.
(2)求当时,x的值.
(3)在平面直角坐标系中画出y与x之间的函数图像,从图像中你还能得到哪些信息?写出一条即可.
【答案】(1)
(2)6
(3)见解析
【分析】(1)根据燃烧速度与总长度即可直接写出关系式,当总长烧完时对应的时间即为时间上限;
(2)将代入求出的解析式即可求解.
(3)根据(1)中求出的解析式,令x=0得出图像与y轴的交点,令y=0得出图像与x轴的交点,再连接并延长即可,再根据图像作答即可.
(1)
由题意得,y与x之间的函数关系式为,
∵,
∴,
∴自变量的取值范围是;
(2)
当时,,
解得;
(3)
当时,,
当时,,
解得,
∴画出的大致函数图像如图所示,
由图像可知,蜡烛7.5小时就燃烧完.
【点睛】本题考查一次函数与实际问题的应用、一次函数图像的画法,根据题意找出函数关系式,找到图像与坐标轴的交点是关键.
易错点三 一次函数图象与坐标轴的交点位置不明确时忘记分类讨论
例题:(2022·浙江金华·八年级期末)如图,直线y=2x+4与x轴交于点A,与y轴交于点B.
(1)求A,B两点的坐标.
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求直线BP的函数关系式.
【答案】(1)A(-2,0),B(0,4)
(2)y=x+4或者y=-x+4
【分析】(1)分别当x=0时和当y=0时,即可求出B、A的坐标;
(2)设P点坐标为(a,0),即,根据OP=2OA,可得,即a=±4,分a=4和a=-4两种情况讨论,用待定系数法求解即可.
(1)
当x=0时,y=2x+4=4,
即B点坐标为(0,4),
当y=0时,0=2x+4,即x=-2,
即A点坐标为(-2,0),
故答案为:B点坐标为(0,4),A点坐标为(-2,0);
(2)
∵P点在x轴上,
∴设P点坐标为(a,0),即,
∵A点坐标为(-2,0),
∴OA=2,
∵OP=2OA,
∴OP=4,
∴,
即a=±4,
当a=4时,P点坐标为(4,0),
设BP的函数关系式为,
∵B点坐标为(0,4),P点坐标为(4,0),
∴,解得,
即此时BP的函数关系式为,
当a=-4时,P点坐标为(-4,0),
同理可求:BP的函数关系式为,
综上:BP的函数关系式为或者.
【点睛】本题考查了求解一次函数与坐标轴交点以及求解一次函数解析式的知识,解题时要注重分类讨论的思想,注意不要遗漏.
【变式训练】
1.(2022·山东·宁津县大庄中学八年级阶段练习)在平面直角坐标系中,O为原点,直线y=kx+b交x轴于A(-3,0),交y轴于B,且三角形AOB的面积为6,则k=________.
【答案】
【分析】由直线过A点(-3,0),可得OA=3,,即,再由直线交y轴于B点,可得B点坐标为(0,b),即,结合,可得,即有,则k值可求.
【详解】∵直线过A点(-3,0),
∴OA=3,,
即,
∵直线交y轴于B点,
∴当x=0,有,
∴B点坐标为(0,b),即,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】本题主要一次函数与坐标轴交点的问题以及坐标系中三角形面积的问题,掌握一次函数的图像与性质是解答本题的关键.
2.(2022·河南·清丰巩营乡二中八年级期末)已知一次函数的图象经过点A(3,0),与轴交于点B,O为坐标原点. 若△AOB的面积为6,则该一次函数的解析式为_____________ .
【答案】或
【分析】分两种情况:当点B在y轴正半轴时,当点B在y轴负半轴时,然后利用待定系数法进行计算即可解答.
【详解】解:点,
,
的面积为6,
,
,
,
或,
将,代入得:
,解得:,
一次函数的解析式为:,
将,代入得:
,解得:,
一次函数的解析式为:,
综上所述:一次函数的解析式为:或,
故答案为:或.
【点睛】本题考查了待定系数法求一次函数解析式,一次函数的性质,一次函数图象上点的坐标特征,分两种情况讨论是解题的关键.
3.(2022·湖北·宜昌市长江中学九年级开学考试)在平面直角坐标系中,直线与轴、轴交于点A、B,点C在x轴负半轴上,若为等腰三角形,则点C的坐标为_______.
【答案】(-4,0)或(-1,0)##(-1,0)或(-4,0)
【分析】由直线解析式求得A、B的坐标,由点A,B的坐标可求出AB的长,分BA=BC、BA=CA种情况讨论求得即可.
【详解】解:直线与x轴、y轴交于点A、B,则点A的坐标为(4,0),点B的坐标为(0,3),
∴AB==5.
分两种情况考虑,如图所示.
①当BA=BC时,OC=OA=4,
∴点的坐标为(-4,0);
②当AB=AC时,∵AB=5,OA=4,点C在x轴负半轴,
∴OC=5-4=1,
∴点的坐标为(-1,0).
∴点C的坐标为(-4,0)或(-1,0),
故答案为:(-4,0)或(-1,0).
【点睛】本题考查了一次函数图象上点的坐标特征、等腰三角形的性质以及勾股定理,分类讨论是解题的关键.
4.(2022·黑龙江齐齐哈尔·八年级期末)在平面直角坐标系中,点是坐标原点,过点的直线与轴交于点,且,则该直线的解析式为___________.
【答案】或
【分析】先表示出点坐标;再把代入得,则,然后根据三角形面积公式得到,即,然后解方程即可求得的值,进一步求得的值.
【详解】解:把代入得,解得,
∴,
∵点在直线上,
∴,
∴,
又∵,
∴,
即:,
∴,
解得:或,
∴当时,,
当时,,
∴该直线的解析式为或.
【点睛】本题考查了一次函数图像上点的坐标特征:一次函数的图像上的点满足解析式.
5.(2022·黑龙江·哈尔滨市第六十九中学校九年级阶段练习)平面直角坐标系内一点,过A点的直线l与x轴相交所成的锐角等于45°,直线l与y轴交于点C,则C点坐标为______.
【答案】或
【分析】根据题意画出图形,然后分类讨论即可.
【详解】解:∵过A点的直线l与x轴相交所成的锐角等于45°,如图:
当直线l在的位置时,设的解析式为:,
将点代入得,,解得,
∴的解析式为:,
当时,,
∴与y轴的交点,
当直线l在的位置时,设的解析式为:,
将点代入得,,解得,
∴的解析式为:,
当时,,
∴与y轴的交点,
综上:C点坐标为或,
故答案为:或.
【点睛】本题考查了待定系数法求一次函数解析式,一次函数的性质,熟练掌握一次函数的性质,运用分类讨论的思想解题是关键.
6.(2022·安徽安庆·八年级期中)直线与直线分别交轴于,两点,两直线相交于轴上同一点.
(1)________
(2)若,点的坐标是______________
【答案】 或
【分析】根据两直线相交同一点,则横坐标相同,即可;设的坐标为:,根据,则,解出,即可.
【详解】∵直线和直线相交轴上同一点
∴,
∴直线与轴的交点为,直线与轴的交点为
∴
∴;
设的坐标为:
∵
∴
∵直线与直线分别交轴于,两点
∴点,
∴
∴
∴
∴点的坐标为或.
故答案为:;或.
【点睛】本题考查一次函数的知识,解题的关键是掌握一次函数图象与性质.
7.(2022·广东·深圳市福田区外国语学校八年级期中)如图,直线与x轴和y轴分别交于两点,射线于点A,若点C是射线上的一个动点,点D是x轴上的一个动点,且以为顶点的三角形与全等,则的长为___________.
【答案】14或16##16或14
【分析】构造一线三直角模型全等一次,为斜边全等一次,得到两个答案.
【详解】因为直线与x轴和y轴分别交于A、B两点,
所以,
所以,
所以,
因为以C、D、A为顶点的三角形与全等,如图,
所以当时,
所以,
所以;
当时,
所以,
所以;
故答案为:14或16.
【点睛】本题考查了一次函数与坐标轴的交点,三角形全等的性质,熟练掌握一次函数与坐标轴的交点是解题的关键.
8.(2022·江苏·盛泽一中八年级阶段练习)已知一次函数的图象经过、,的面积为2,求该一次函数的解析式.
【答案】一次函数解析式为或.
【分析】因为的面积为2,图象经过、,所以a有两个值,4或,再用待定系数法求出一次函数解析式.
【详解】解:∵,、,
∴,
∴,
∴A点的坐标为或.
①把,代入,
∴,
解得,
∴一次函数解析式为;
②把A,代入,
同理得到一次函数解析式为,
适合条件的一次函数解析式为:或.
【点睛】本题考查了待定系数法求出一次函数解析式.也考查了三角形的面积公式以及分类讨论的思想运用.
9.(2022·全国·八年级课时练习)如图,直线与x轴、y轴分别交于点,点P在x轴上运动,连接,将沿直线折叠,点O的对应点记为.
(1)求k、b的值;
(2)在x轴上是否存在点C,使得为等腰三角形?若存在,求出点C的坐标;若不存在,说明理由.
(3)若点恰好落在直线上,求的面积.
【答案】(1)
(2)存在,或或或
(3)或
【分析】(1)用待定系数法直接求出;
(2)分三种情形讨论,①当时,②当时,③当时;分别求出即可;
(3)分P在x轴的正半轴和负半轴:①当P在x轴的正半轴时,求,根据三角形面积公式可得结论;
②当P在x轴的负半轴时,同理可得结论.
【详解】(1)解:∵点在直线上,
∴,
解得:;
(2)解:存在,理由如下:如图1所示,
①当时,,
可得.
②当时,,可得.
③当时,点C与点O重合,可得,
综上所述,满足条件的点C坐标为或或或.
(3)解:存在两种情况:①当P在x轴的正半轴上时,如图2所示:
点恰好落在直线上,则,,
∵,
∴是等腰直角三角形,
∴,
由折叠得:,
∴,
∴,
∴,
中,,
∴;
②当P在x轴的负半轴时,如图3所示:
由折叠得:,,
∵,
∴,
∴;
综上所述,的面积为或.
【点睛】此题是一次函数综合题,考查了待定系数法、坐标与图形性质、折叠的性质、勾股定理、等腰直角三角形的判定与性质、三角形的面积公式、等腰三角形的性质以及分类讨论等知识;本题综合性强,熟练掌握待定系数法和等腰三角形的性质,进行分类讨论是解题的关键.
x
0
40
y=24-0.6x
24
0
相关试卷
这是一份浙教版数学八上期末专题训练专题10 易错易混集训:勾股定理(2份,原卷版+解析版),文件包含浙教版数学八上期末专题训练专题10易错易混集训勾股定理原卷版doc、浙教版数学八上期末专题训练专题10易错易混集训勾股定理解析版doc等2份试卷配套教学资源,其中试卷共28页, 欢迎下载使用。
这是一份苏科版八年级数学上册重难点专题提优训练专题20易错易混集训:一次函数(原卷版+解析),共26页。试卷主要包含了忽略自变量的取值范围致错等内容,欢迎下载使用。
这是一份苏科版八年级数学上册重难点专题提优训练专题11易错易混集训:勾股定理(原卷版+解析),共20页。









