



所属成套资源:苏科版数学八上期末专题复习专题 (2份,原卷版+解析版)
- 苏科版数学八上期末专题复习专题10 全等三角形七大重难模型(期末真题精选)(2份,原卷版+解析版) 试卷 0 次下载
- 苏科版数学八上期末专题复习专题11 最值之将军饮马(期末真题精选)(2份,原卷版+解析版) 试卷 0 次下载
- 苏科版数学八上期末专题复习专题12 轴对称30大高频考点(期末真题精选)(2份,原卷版+解析版) 试卷 1 次下载
- 苏科版数学八上期末专题复习专题14 实数重难考点分类练(七大考点)(期末真题精选 )(2份,原卷版+解析版) 试卷 0 次下载
- 苏科版数学八上期末专题复习专题15 平面直角坐标系与一次函数重难考点分类练(十五大考点)(2份,原卷版+解析版) 试卷 1 次下载
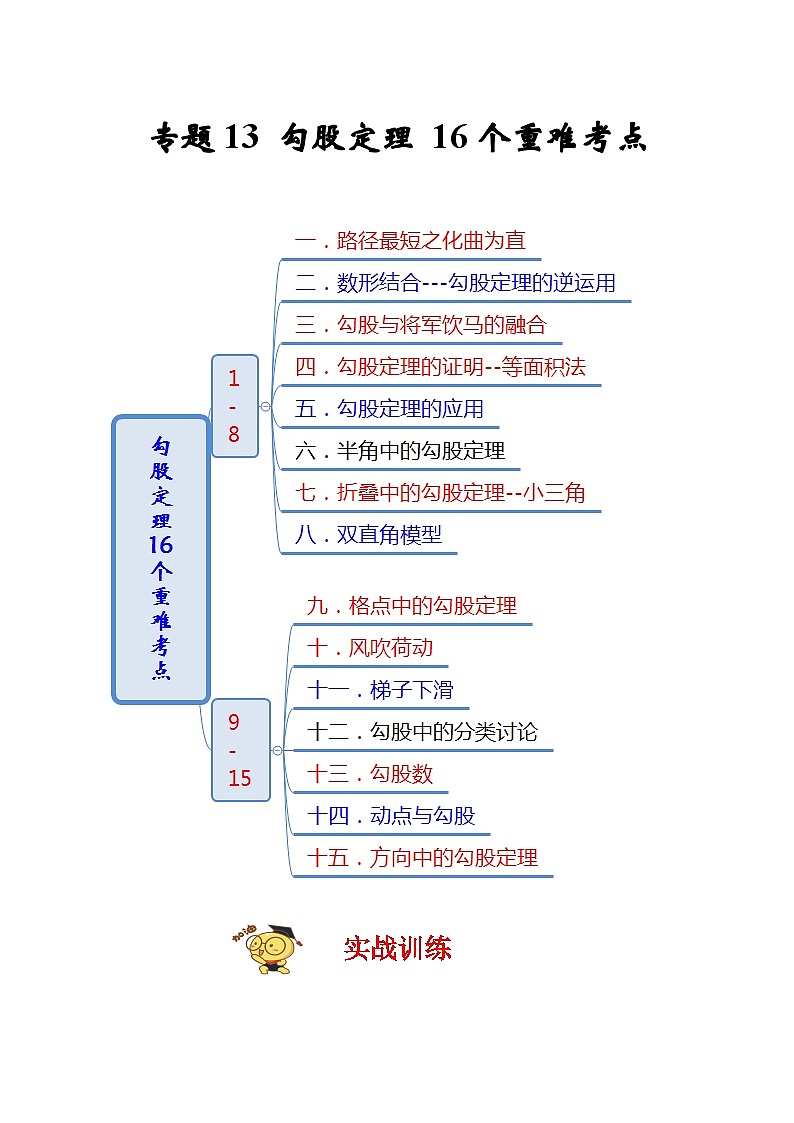
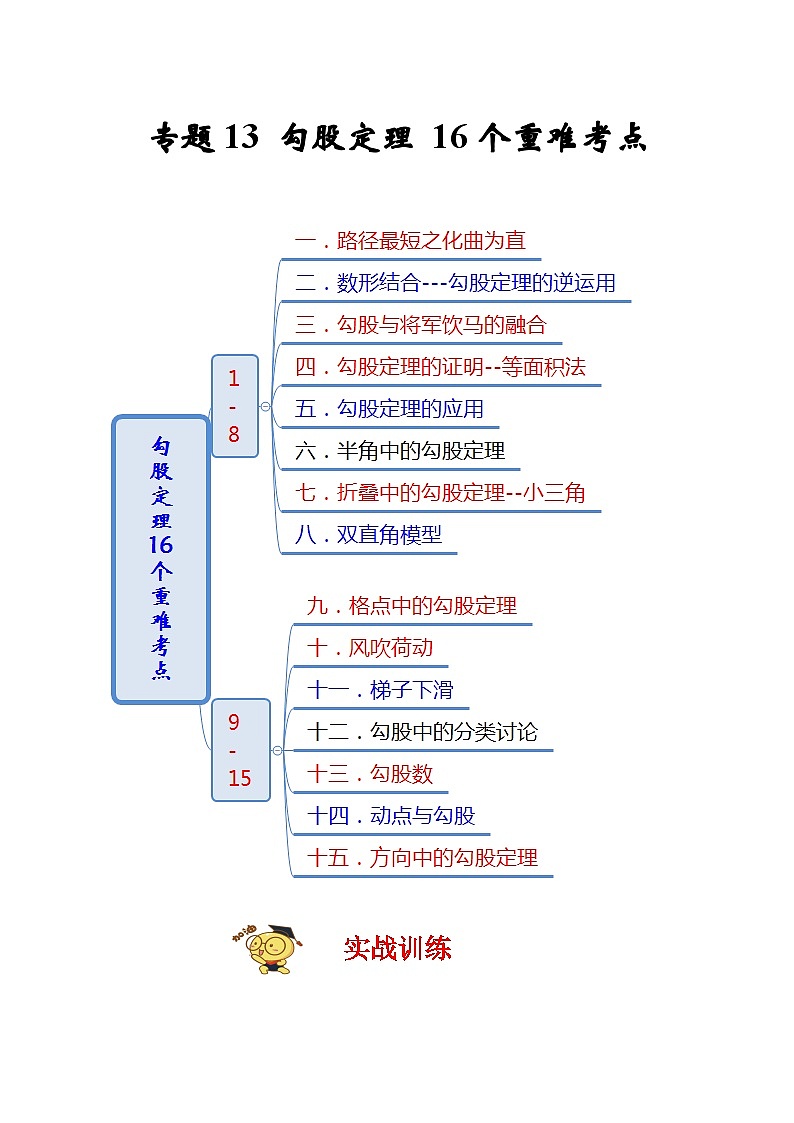
苏科版数学八上期末专题复习专题13 勾股定理16个重难考点(期末真题精选)(2份,原卷版+解析版)
展开
这是一份苏科版数学八上期末专题复习专题13 勾股定理16个重难考点(期末真题精选)(2份,原卷版+解析版),文件包含苏科版数学八上期末专题复习专题13勾股定理16个重难考点期末真题精选原卷版doc、苏科版数学八上期末专题复习专题13勾股定理16个重难考点期末真题精选解析版doc等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
实战训练
一.路径最短之化曲为直
1.为了庆祝国庆,学校准备在教学楼大厅的圆柱体柱子上贴彩带,已知柱子的底面周长为lm,高为3m.如果要求彩带从柱子底端的A处绕柱子4圈后到达柱子顶端的B处,那么至少应购买彩带 米.
2.如图:一个圆柱的底面周长为16cm,高为6cm,BC是上底面的直径,一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,则蚂蚁爬行的最短路程为 cm.
3.如图,一只蚂蚁从长、宽都是4,高是6的长方体纸箱的A点沿纸箱表面爬到B点,那么它所行的最短路线的长是 .
二.数形结合---勾股定理的逆运用
4.如果三角形的三边a,b,c满足a2+b2+c2+50=6a+8b+10c,则此三角形的周长为 .
5.若△ABC的三边a、b、c满足a2+b2+c2+50=6a+8b+10c,则这个三角形最长边上的高是多少?
6.已知,在△ABC中,三条边长分别是a、b、c,且a=n2﹣1,b=2n,c=n2+1(n>1),求证:∠C=90°.
7.|x﹣12|+|x+y﹣25|与z2﹣10z+25互为相反数,那么以x、y、z为边的三角形是什么三角形?
三.勾股与将军饮马的融合
8.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
9.如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为 cm(假设蜂蜜不会下滑).
四.勾股定理的证明--等面积法
10.三国时代东吴数学家赵爽(字君卿,约公元3世纪)在《勾股圆方图注》一书中用割补的方法构造了“弦图”(如图1),并给出了勾股定理的证明.已知,图2中涂色部分是直角边长为a,b,斜边长为c的4个直角三角形,请根据图2利用割补的方法验证勾股定理.
11.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,也可以用面积法来证明,请将下面说理过程补充完整:
证明:连接DB,过点D作BC边上的高DF,交BC的延长线于点F,
则四边形DFCE为长方形,所以DF=EC= .(用含字母的代数式表示)
因为S四边形ABCD=S△ACD+ = ;
S四边形ABCD=S△ADB+ ;
所以 ;
所以 .
12.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中,∠ACB=90°,BC=a,AC=b,AB=c,正方形IECF中,IE=EC=CF=FI=x.
(1)小明发明了求正方形边长的方法:
由题意可得BD=BE=a﹣x,AD=AF=b﹣x.
因为AB=BD+AD,所以a﹣x+b﹣x=c,解得x= .
(2)小亮也发现了另一种求正方形边长的方法:连接IC,利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系,请根据小亮的思路完成他的求解过程;
(3)请结合小明和小亮得到的结论验证勾股定理.(注:根据比例的基本性质,由可得ad=bc)
五.勾股定理的应用
13.在△ABC中,BC=a,AC=b,AB=c,设c为最长边.当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,可以判断△ABC的形状(按角分类).
(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为 三角形;当△ABC三边长分别为6,8,11时,△ABC为 三角形.
(2)小明同学根据上述探究,有下面的猜想:“当a2+b2>c2时,△ABC为锐角三角形;当a2+b2<c2时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:
当a=2,b=3时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
六.半角中的勾股定理
14.已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径的长等于CA的扇形CEF绕点C旋转,且直线CE,CF分别与直线AB交于点M,N.
(Ⅰ)当扇形CEF绕点C在∠ACB的内部旋转时,如图1,求证:MN2=AM2+BN2;
(思路点拨:考虑MN2=AM2+BN2符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM沿直线CE对折,得△DCM,连DN,只需证DN=BN,∠MDN=90°就可以了.请你完成证明过程.)
(Ⅱ)当扇形CEF绕点C旋转至图2的位置时,关系式MN2=AM2+BN2是否仍然成立?若成立,请证明;若不成立,请说明理由.
七.折叠中的勾股定理--小三角
15.在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片使点A落在边BC上的A'处,折痕为PQ.当点A'在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点B与点A'间的最小距离为 .
16.如图,将长方形纸条ABCD沿EF,GH折叠,使点B,C两点恰好都落在AD边的P点处.若BC=10cm,则△PFH的周长为 cm.
八.双直角模型
17.如图,在△ABC中,D是BC上一点,若AB=10,BD=6,AD=8,AC=17.
(1)求证:△ABD是直角三角形;
(2)求△ADC的面积.
18.如图,在一块四边形ABCD空地种植草皮,测得AB=3m,BC=4m,DA=13m,CD=12m,且∠ABC=90°.若每平方米草皮需要200元,则需要投资多少钱?
九.格点中的勾股定理
19.如图,每个小正方形的边长都为1.
(1)分别求出AB,BC,AC的长;
(2)求△ABC的面积.
20.如图正方形网格中的△ABC,若小方格边长为1,请你根据所学的知识判断△ABC是什么形状?并说明理由.
十.风吹荷动
21.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了多少米.
22.小颖爸爸为了丰富活动,为小区里的小朋友们搭了一架简易秋千(如图),秋千AB在静止位置时,下端B距离地面0.6m,即OB=0.6m,当秋千荡到AC的位置时,下端C距离地面1.4m,即CD=1.4m,与静止位置的水平距离OD=2.4m,求秋千AB的长.
十一.梯子下滑
23.有一梯子长25米,靠在垂直的墙面上,梯子的跟部离墙的底部是7米,若梯子顶部下滑4米,那么梯子跟部到墙的底部的距离是多少米?
24.如图,在△ABC中,CE是AB边上的中线,CD⊥AB于D,且AB=5,BC=4,AC=6,求DE的长.
十二.勾股中的分类讨论
25.若直角三角形的两边长分别为3和4,则第三条边的长的平方为 .
26.已知m,n为一个直角三角形的两边的长度,且(m﹣2)2+|n﹣3|=0,则该直角三角形第三条边的长度为 .
十三.勾股数
27.我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数: ;
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为 和 .
十四.动点与勾股
28.如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒4cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
29.如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,同时停止.
(1)P、Q出发4秒后,求PQ的长;
(2)当点Q在边CA上运动时,出发几秒钟后,△CQB能形成直角三角形?
十五.方向中的勾股定理
30.一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向航行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处.若M,N两点相距100海里,则∠NOF的度数为( )
A.50°B.60°C.70°D.90°
31.如图,甲船以20海里/时的速度从港口O出发向西北方向航行,乙船以15海里/时的速度同时从港口O出发向东北方向航行,则2小时后,两船相距( )
A.40海里B.45海里C.50海里D.55海里
相关试卷
这是一份苏科版数学八上期末专题复习专题05 翻折变换精选(2份,原卷版+解析版),文件包含苏科版数学八上期末专题复习专题05翻折变换精选原卷版doc、苏科版数学八上期末专题复习专题05翻折变换精选解析版doc等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
这是一份苏科版数学八上期末专题复习专题02 作图精选(2份,原卷版+解析版),文件包含苏科版数学八上期末专题复习专题02作图精选原卷版doc、苏科版数学八上期末专题复习专题02作图精选解析版doc等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
这是一份苏科版数学八上期末专题复习专题01 填空选择压轴精选50道(2份,原卷版+解析版),文件包含苏科版数学八上期末专题复习专题01填空选择压轴精选50道原卷版doc、苏科版数学八上期末专题复习专题01填空选择压轴精选50道解析版doc等2份试卷配套教学资源,其中试卷共65页, 欢迎下载使用。









