北师大版（2024）九年级上册3 反比例函数的应用课文ppt课件

这是一份北师大版（2024）九年级上册3 反比例函数的应用课文ppt课件，共23页。PPT课件主要包含了观察与思考，典例精析，变形得，小组讨论，做一做，Smm2，P432，方法归纳，至多3cm等内容，欢迎下载使用。
1.会根据实际问题中变量之间的关系,建立反比例函数模型;（重点）2.能利用反比例函数解决实际问题．（难点）
问题:使劲踩气球时，气球为什么会爆炸？
在温度不变的情况下，气球内气体的压强p与它的体积V 的乘积是一个常数k.
即 pV=k(k为常数，k＞0).
反比例函数在实际生活中的应用
例1：某校科技小组进行野外考察，利用铺垫木板的方式通过一片烂泥湿地，你能解释他们这样做的道理吗？当人和木板对湿地的压力一定时，随着木板面积S(m2)的变化，人和木板对地面的压强p (Pa)将如何变化？如果人和木板对湿地地面的压力合计600N，那么(1)用含S的代数式表示p，p是S的反比例函数吗？为什么？
由p＝ 得p＝p是S的反比例函数，因为给定一个S的值，对应的就有唯一的一个p值和它对应，根据函数定义，则p是S的反比例函数．
(2)当木板面积为0.2m2时，压强是多少？
当S＝0.2m2时，p＝ ＝3000(Pa) ．答：当木板面积为0.2m2时压强是3000Pa．
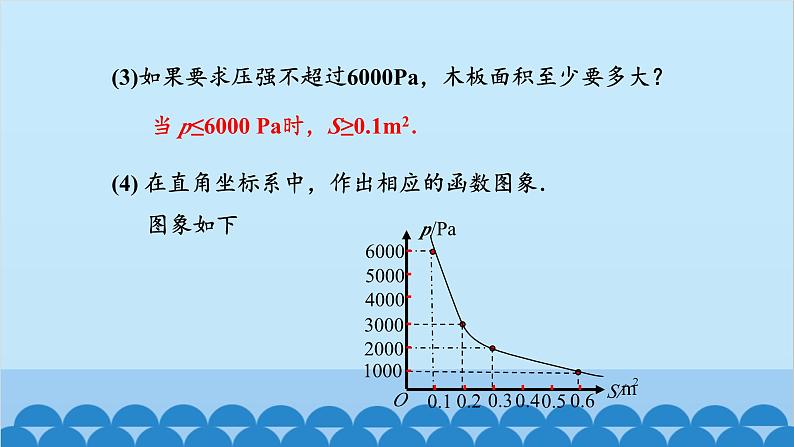
(3)如果要求压强不超过6000Pa，木板面积至少要多大？
(4) 在直角坐标系中，作出相应的函数图象． 图象如下
当 p≤6000 Pa时，S≥0.1m2．
例1.市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室.(1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?(2)公司决定把储存室的底面积S定为500 m2,施工队施工时应该向下掘进多深?(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?
(1)根据圆柱体的体积公式,我们有 S×d=
即储存室的底面积S是其深度d的反比例函数.
市煤气公司要在地下修建一个容积为104 m3的圆柱形煤气储存室. (1)储存室的底面积S(单位:m2)与其深度d(单位:m)有怎样的函数关系?
把S=500代入 ,得
解得 d=20 如果把储存室的底面积定为500m²,施工时应向地下掘进20m深.
(2)公司决定把储存室的底面积S定为500 m²，施工队施工时应该向下掘进多深?
根据题意,把d=15代入 ,得
解得 S≈666.67
当储存室的深为15m时,储存室的底面积应改为666.67m²才能满足需要.
(3)当施工队按(2)中的计划掘进到地下15m时,碰上了坚硬的岩石.为了节约建设资金,储存室的底面积应改为多少才能满足需要(保留两位小数)?
圆柱体的体积公式是什么？第（2）问和第（3）问与过去所学的解分式方程和求代数式的值的问题有何联系？
【反思小结】（1）问首先要弄清此题中各数量间的关系，容积为104，底面积是S，深度为d，满足基本公式：圆柱的体积＝底面积×高，由题意知S是函数，d是自变量，改写后所得的函数关系式是反比例函数的形式.（2）问实际上是已知函数S的值，求自变量d的取值，（3）问则是与（2）相反．
我们学习过反比例函数，例如，当矩形面积一定时，长a是宽b的反比例函数，其函数解析式可以写为 （S为常数，S≠0）．请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例，并写出它的函数解析式．实例： ；函数解析式： ．
练一练：你吃过拉面吗？一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细（横截面积） S(mm2)的反比例函数．其图象如图所示，则当面条粗1.6mm2时，面条的总长度是多少米？
反比例函数在物理问题中的应用
物理中也有一些问题是与反比例函数息息相关的，一起来看看下面的例子．
(1)蓄电池的电压是多少？你能写出这一函数的表达式吗？
解： (1)由题意设函数表达式为 I＝ ∵A(9，4)在图象上，∴U＝IR＝36．∴表达式为I＝ ．即蓄电池的电压是36V．
(2)完成下表，并回答问题：如果以此蓄电池为电源的用电器限制电流不得超过10A，那么用电器的可变电阻应控制在什么范围内？
解：当I≤10A时,解得R≥3.6Ω.所以可变电阻应不小于3.6Ω．
反比例函数应用的常用解题思路是：（1）根据题意确定反比例函数关系式：（2）由反比例关系式及题中条件去解决实际问题．
(1)当矩形的长为12cm时，宽为　　　　，当矩形的宽为4cm，其长为　　　　　.(2) 如果要求矩形的长不小于8cm，其宽　　　　　.
1.已知矩形的面积为24cm2，则它的长y与宽x之间的关系用图象大致可表示为（ ）
2.某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数，其图象如图所示，当气球内的气压大于120kPa时，气球将爆炸．为了安全起见，气球的体积应（ ） A. 不大于 B. 小于 C. 不小于 D. 大于
3.码头工人以每天30吨的速度往一艘轮船上装载货物，把货物装载完毕恰好用了8天时间．货物到达目的地后开始卸货，则：（1）卸货速度v(吨/天)与卸货时间t(天)之间有怎样的函数关系？（2）由于遇到紧急情况，船上的货物必须不超过5日卸载完毕，那么平均每天至少要卸多少吨货物？
解析：(1)从题设中我们不难发现：v和t之间的函数关系，实际上是卸货速度和卸货时间的关系，根据卸货速度＝货物总量÷卸货时间，就可得到v和t的函数关系，根据题中每天以30吨的速度往一艘轮船上装载货物，把货物装载完毕恰好用了8天时间．根据装货速度×装货时间＝货物总量，可以求出轮船装载货物的总量，即货物的总量为30×8＝240(吨)．所以v与t的函数表达式为
(2)由于遇到紧急情况，船上的货物必须在不超过5日内卸载完毕，求平均每天卸载货物至少多少吨．即求当t≤5时，v至少为多少吨．由 得 ，t≤5，所以 ≤5 .因为v>0，所以240≤5v，解得v≥48，所以船上的货物要在不超过5日内卸载完毕，平均每天至少卸载48吨货物．