高中数学人教A版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.3 空间向量及其运算的坐标表示教学设计

这是一份高中数学人教A版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.3 空间向量及其运算的坐标表示教学设计，共10页。教案主要包含了教学目标，学习目标，教学重难点，教学过程等内容，欢迎下载使用。

一、教学目标
1.通过与平面向量类比学习并掌握空间向量加法、减法、数乘、数量积运算的坐标表示以及向量的长度、夹角公式的坐标表示，并能初步应用这些知识解决简单的立体几何问题.
2.通过将空间向量运算与熟悉的平面向量的运算进行类比，使学生掌握空间向量运算的坐标表示，渗透类比的数学方法.
3.会用空间向量运算的坐标表示解决简单的立体几何问题，体会向量方法在研究空间图形中的作用，培养学生的空间想象能力和几何直观能力.

二、学习目标
1.掌握空间向量加减、数乘、数量积运算的坐标表示.
2.会根据向量的坐标，判断两个向量共线或垂直.
3.掌握向量的长度公式、两向量夹角公式、空间两点间距离公式;并会应用这些知识解决简单的立体几何问题.

三、教学重难点
重点：空间向量运算的坐标表示.
难点：应用空间向量解决简单的立体几何问题.

四、教学过程
（一）创设情境
前面我们通过引入空间直角坐标系，将空间向量的坐标与空间点的坐标一一对应起来.
那么有了空间向量的坐标表示，类比平面向量的坐标运算，同学们是否可以探究出空间向量的坐标表示并给出证明呢？
师生活动：教师利用生活中的较常见的实例引导学生思考，让学生建立空间直角坐标系，提出问题，引导学生思考如何将其数学化，用空间向量的坐标来表示.
设计意图：通过结合身边的事物引出数学知识，学生会感到亲切、生动、真实、易于接受. 同时，能使他们体会到生活中处处有数学，数学就在我们身边，我们生活在充满数学信息的现实世界中. 能促进学生会用数学的眼光去观察和认识周围的事物，有效的促进知识的迁移.
（二）探究新知
任务1：探究空间向量的坐标运算
思考1：类比平面向量的坐标运算，你能得出空间向量运算的坐标表示并给出证明吗?
合作探究：1.先独立将空间坐标运算的表示和证明写出来；
2.小组内相互对照并交流讨论自己写的空间向量坐标运算和证明；
3.以小组为单位进行展示汇报.
探究1：你能证明空间向量数量积运算的坐标表示吗？
要求：以小组为单位进行讨论交流，并汇报
设i，j，k为空间的一个单位正交基底，则
a= a1i+a2j+a3k ， b= b1i+b2j+b3k
所以a∙b=a1i+a2j+a3k ∙ b1i+b2j+b3k
利用向量数量积的分配率以及
i∙i=j∙j=k∙k=1，i∙j∙k=0
得a∙b=a1∙b1+a2∙b2+a3∙b3
思考2：空间向量运算的坐标表示与平面向量运算的坐标表示一样吗？
由上述结论可知，空间向量运算的坐标表示与平面向量运算的坐标表示是完全一致的．例如，我们有:
一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标.
任务2：探究空间向量平行、垂直、模和夹角
思考3：平面向量的坐标可以用于表示向量平行、垂直等特殊位置关系，以及解决关于长度、夹角等的计算问题，空间向量呢?
答：平面向量共线与垂直判定已知a=a1，a2，a3，b=b1，b2，b3
已知a=a1，a2，b=b1，b2
空间向量共线与垂直判定
类
比
a∥b⇔a=λbb≠0
⇔a1=λb1，a2=λb2，a3=λb3
a⊥b⇔a1b1+a2b2+a3b3=0
a∥b⇔a1b2−a2b1=0
当b≠0时，a1b1=a2b2
a⊥b⇔a1b1+a2b2=0
思考4：设a=a1，a2，a3，b=b1，b2，b3，
a∥bb≠0⇔a1=λb1a2=λb2a3=λb3λ∈R能否换成a1b1=a2b2=a3b3？
答：不能。因为只有当b1，b2，b3都不为0时，a1b1=a2b2=a3b3才有意义，
而b≠0⇔b1，b2，b3至少有一个不为0.
所以，当b1，b2，b3都不为0时，a∥b⇔a1b1=a2b2=a3b3.
思考5：平面向量的坐标可以用于表示向量平行、垂直等特殊位置关系，以及解决关于长度、夹角等的计算问题，空间向量呢?
做一做：1.已知a=2，−3，4，b=−1，3，2，则a+b= ；3a= ；a+2b= ；a∙b= ；a= ； csa，b= .
2.已知向量a=2，−1，3，b=−4，2，x，若a⊥b，则x= ；若a∥b，则x= .
要求：个人先完成，再以小组为单位相互批改，组长汇报组员完成情况
答：1.a+b=2，−3，4+−1，3，2=2−1，−3+3，4+2=1，0，6；
3a=3×2，−3，4=2×3，−3×3，4×3=6，−9，12；
a+2b=2，−3，4+2×−1，3，2=0，3，8；
a∙b=2×−1+−3×3+4×2=−3；
a=22+−32+42=29 ；
csa，b=2×−1+−3×3+4×222+−32+42−12+32+22=−3406406 .
2.∵a⊥b，∴2×−4+−1×2+3x=0，解得x=103；
∵a∥b，∴2a=b，∴x=−6
师生活动：学生理解、记忆、运用公式.
设计意图：通过对公式的推导熟练坐标运算，增强学生应用向量坐标运算的意识.
任务3：探究空间中两点间的距离
探究1：你能利用空间向量运算的坐标表示推导空间两点间的距离公式吗?
要求：以小组为单位进行讨论交流，并汇报
如图1.3-7建立空间直角坐标系Oxyz，设P1=x1，y1，z1，P2=x2，y2，z2是空间中任意两点，则
P1P2=OP2−OP1=x2−x1，y2−y1，z2−z1.
于是
P1P2=P1P2∙P1P2 =x2−x12+y2−y12+z2−z12
所以P1P2=P1P2=x2−x12+y2−y12+z2−z12.
这就是空间两点间的距离公式.
设计意图：通过对公式的推导熟练坐标运算，增强学生应用向量坐标运算的意识.
应用举例
例1 (1)已知a=2，−1，−2，b=0，−1，4，求a+b，2a∙−b，a+b∙a−b.
(2)已知O是坐标原点，点A2，3，−2，B3，2，2，C2，0，7.若点P的坐标能满足AP=2AB−3AC，则点P的坐标为 .
解：(1)a+b=2，−1，−2+0，−1，4=2，−2，2，
2a∙−b=22，−1，−2∙0，1，−4=14，
∵a−b=2，−1，−2−0，−1，4=2，0，−6
∴a+b∙a−b=2，−2，2∙2，0，−6=−8
(2)因为点A2，3，−2，B3，2，2，C2，0，7
所以AB=1，−1，4，AC=0，−3，9
设Px，y，z，则AP=x−2，y−3，z+2
因为AP=2AB−3AC
所以x−2，y−3，z+2=21，−1，4−30，−3，9=2，7，−19
所以x−2=2，y−3=7，z+2=−19
所以点P的坐标为4，10，−21
【总结】关于空间向量坐标运算的两类问题
(1)直接计算问题
首先将空间向量用坐标表示出来，然后准确运用空间向量坐标运算公式计算．
(2)由条件求向量或点的坐标
首先把向量用坐标形式设出来，然后通过建立方程组，解方程求出其坐标．
例2 如图1.3-8，在正方体ABCD−A1B1C1D1中，E、F分别是BB1，D1B1的中点.
求证EF⊥DA1
证明：设正方体的棱长为1，建立空间直角坐标系Oxyz，则E1,1，12，F12，12，1，
所以EF=−12，−12，12
又A11，0，1，D0,0,0，
所以DA1=1，0，1.
所以EF∙DA1=−12，−12，12∙1，0，1=0
所以EF⊥DA1，即EF⊥DA1.
【总结】
例3 如图1.3-9，在棱长为1的正方体ABCD−A1B1C1D1中，M为底面B1C1的中点，E1,F1分别在棱A1B1，C1D1上，B1E1=14A1B1,D1F1=14C1D1.
（1）求AM的长；
（2）求BE1与DF1所成的角的余弦值.
分析：（1）建立空间直角坐标系，求出A，M的坐标，利用空间两点间的距离公式求出AM的长。
（2）BE1与DF1所成的角就是BE1，DF1所成的角或它的补角，因此可以通过BE1，DF1的数量积公式运算得到结果.
解：（1）建立如图1.3-9所示的空间直角坐标系Oxyz，则点A的坐标为1，0，0，点M的坐标为12，1，12.于是
AM=12−12+1−02+12−02=62.
由已知，得：
B1，1，0，E11，34,1，D0,0,0，F10，14,1，
所以BE1=1，34,1−1，1，0=0，−14,1
DF1=0，14,1−0,0,0=0，14,1
BE1=174，DF1=174.
所以BE1∙DF1=0×0+−14×14+1×1=1516
所以csBE1，DF1=BE1∙DF1BE1DF1=1516174×174=1517
所以BE1与DF1所成角的余弦值是1517.
思考：两条直线a，b的夹角θ与其方向向量a，b的夹角相等吗？
答：不一定，它们的取值范围不同.
向量a，b的夹角a，b∈0，π
直线a，b的夹角θ∈0，π2
当a，b∈0，π2时，θ=a，b；当a，b∈π2，π时，θ=π−a，b
所以csθ=csa，b
【总结】求空间中两条直线所成的角的余弦值
求法：空间向量法
步骤：①建立空间直角直坐标系，②求对应线段的向量坐标及模的大小，③利用向量的数量积公式求两条直线所成角的余弦值
总结：求空间内两点之间的距离和两条直线所成的角的余弦值可以建立空间直角坐标系，再利用空间向量去进行解题，这种方法在后面的学习当中会经常用到，比如求空间内的两条直线是否垂直或平行。
例4：已知向量a=(1,1,0)，b=(−1,0,2)．
(1)若(a+kb)//(2a+b)，求实数k:
(2)若向量a+kb与2a+b所成角为锐角，求实数k的范围．
提示：(1)先求向量的坐标，利用平行的条件，即可求k的值；
(2)向量a+kb与2a+b的夹角为锐角，则数量积大于0且不共线，即可求k的取值范围．
解：(1)由题知，a+kb=(1−k,1,2k)，2a+b=(1,2,2)，
那么当(a+kb)//(2a+b)时，1−k1=12=2k2，可得k=12；
(2)由(1)知，a+kb=(1−k,1,2k)，2a+b=(1,2,2)，
那么当向量a+kb与2a+b所成角为锐角时，
(a+kb)⋅(2a+b)=(1−k,1,2k)⋅(1,2,2)=1−k+2+4k>0，
即得k>−1，
又当k=12时，(a+kb)//(2a+b)，
可得实数k的范围为k|k>−1,且k≠12.
设计意图：通过例题，熟悉利用空间向量解决对应问题的方法，并体会将立体几何问题转化为空间向量问题的思想．
课堂练习
1.已知空间向量a=1,m,2,b=1,−5,−3，且a⊥b，则m=( )
A. −1B. 2C. −2D. 1
解：因为a=1,m,2,b=1,−5,−3，
且a⊥b，
所以a⋅b=1−5m−6=0，解得m= −1．
故选：A．
2.已知a=2,−2,−2,b=2,0,4，则csa，b=（ ）
A.31010B.1C.0D.−1515
解：因为a=2,−2,−2,b=2,0,4
可得csa，b=a∙ba∙b=4+0−823×25=−1515
故选D
3.已知a=(1,0,1),b=(0,1,0),c=(1,1,1)，下列选项中正确的是( )
A. b⋅c=3B. a⊥bC. (b+c)//aD. 〈a,b〉=π4
解：已知a=(1,0,1),b=(0,1,0),c=(1,1,1)，
对于A，b⋅c=1，故A错误；
对于B，a⋅b=0，故a⊥b，故B正确；
对于C，b+c=(1,2,1)，不存在实数λ，使得b+c=λa，故b+c与a不平行，故C错误；
对于D，由B的分析可知a⊥b，则⟨a,b⟩=π2，故D错误．
故选B．
4.在棱长为1的正方体ABCD−A1B1C1D1中，E，F分别是D1D，BD的中点，G在棱CD上，且CG=14CD，H是C1G的中点．
(1)求EF与B1C所成的角;
(2)求EF与C1G所成角的余弦值．
解：根据题意建立如图所示的空间直角坐标系Dxyz，
则D(0,0,0)，E(0,0,12)，F(12,12,0)，C(0,1,0)，C1(0,1,1)，B1(1,1,1)，G(0,34,0)．
(1)易得EF=(12,12,−12)，B1C=(−1,0,−1)，
∴EF⋅B1C=12×(−1)+12×0+(−12)×(−1)=0．
∴EF⊥B1C，
即EF⊥B1C，
∴EF与B1C所成的角为90∘．
(2)易得C1G=(0,−14,−1)，∴|C1G|= 174．
由(1)可知|EF|= 32，
且EF⋅C1G=38，
∴cs=EF⋅C1G|EF||C1G|= 5117，
即EF与C1G所成角的余弦值为 5117．
试题ID: 3fd7bfe1-eb5b-4ec6-87d2-ca2922ee03d5
5.如图所示，在底面是矩形的四棱锥P−ABCD中，PA⊥底面ABCD,E,F分别是PC,PD的中点，PA=AB=1,BC=2．
(1)求B,F两点间的距离；
(2)求证：EF//平面PAB；
(3)求证：平面PAD⊥平面PDC．
解：(1)由题可知，PA⊥底面ABCD，AB，AD⊂平面ABCD，所以PA⊥AB，PA⊥CD，又AB⊥AD，以A为原点，AB所在直线为x轴，AD所在直线为y轴，AP所在直线为z轴，建立如图所示的空间直角坐标系，
则A0,0,0,B1,0,0,C1,2,0,D0,2,0,P0,0,1，
∴E12,1,12,F0,1,12,BF=−1,1,12,BF=32，
即B,F两点间的距离为32．
(2)由(1)知，EF=−12,0,0,AP=0,0,1,AD=0,2,0,DC=1,0,0,AB=1,0,0，
所以EF=−12AB，即EF//AB，即EF//AB，
又AB⊂平面PAB,EF⊄平面PAB，
所以EF//平面PAB．
(3)由(2)知，AP=0,0,1，AD=0,2,0，DC=1,0,0，
所以AP⋅DC=0,0,1⋅1,0,0=0，AD⋅DC=0,2,0⋅1,0,0=0，
则AP⊥DC,AD⊥DC，即AP⊥DC,AD⊥DC，
又AP∩AD=A，且AP,AD⊂平面PAD，
所以DC⊥平面PAD，
又DC⊂平面PDC，
所以平面PAD⊥平面PDC．
设计意图：通过课堂练习，让学生反复巩固空间向量在解决立体几何问题的方法，并能够灵活运用.
（五）归纳总结
【课堂小结】回顾本节课的内容，你都学到了什么？
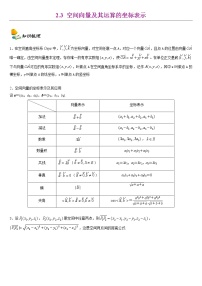
平面向量的坐标运算表示
空间向量的坐标运算表示
设a=a1，a2，b=b1，b2，
a+b=a1+b1，a2+b2
a−b=a1−b1，a2−b2
λa=λa1，λa2，λ∈R
a∙b=a1∙b1+a2∙b2
对应坐标相加
设a=a1，a2，a3，b=b1，b2，b3，
对应坐标相减
a+b=a1+b1，a2+b2，a3+b3
每个坐标乘λ
a−b=a1−b1，a2−b2，a3−b3
λa=λa1，λa2，λa3，λ∈R
对应坐标乘积的和
a∙b=a1∙b1+a2∙b2+a3∙b3
平面向量长度、夹角的坐标表示
空间向量长度、夹角的坐标表示
设a=a1，a2，b=b1，b2
设a=a1，a2，a3，b=b1，b2，b3
a=a∙a=a12+a22
a=a∙a=a12+a22+a32
csa，b=a∙bab=a1∙b1+a2∙b2a12+a22b12+b22
csa，b=a∙bab=a1∙b1+a2∙b2+a3∙b3a12+a22+a32b12+b22+b32