北师大版（2024）七年级上册（2024）2 从立体图形到平面图形完美版备课课件ppt

这是一份北师大版（2024）七年级上册（2024）2 从立体图形到平面图形完美版备课课件ppt，共40页。PPT课件主要包含了学习目标，情景导入，新知探究，缺底面，两个底面重叠，观察思考，回顾反思，概念归纳，练一练，三棱锥的平面展开图等内容，欢迎下载使用。

1.通过展开与折叠活动，了解棱柱、圆柱和圆锥的展开图.（重点）2.能根据展开图判断和制作简单的立体模型. （难点）3.经历展开与折叠、模型制作等活动，发展空间观念，积累数学活动经验.
想一想，这些精美的包装盒是怎样制成的？
要设计、制作一个包装盒，除了美术设计以外，还要了解它展开后的形状，根据它的展开图来裁剪纸张。
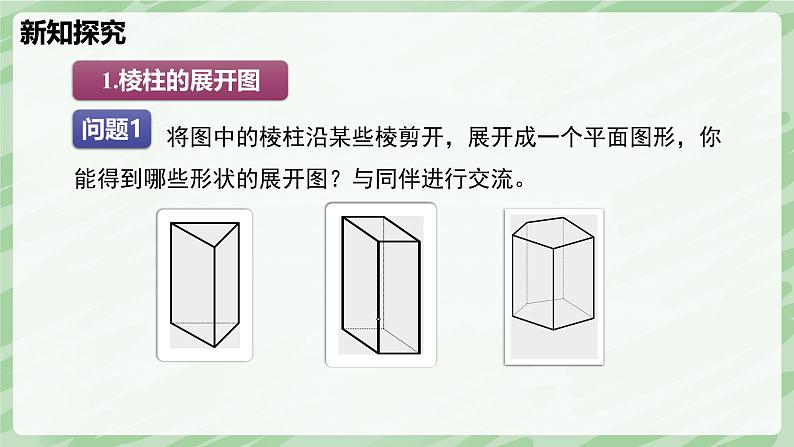
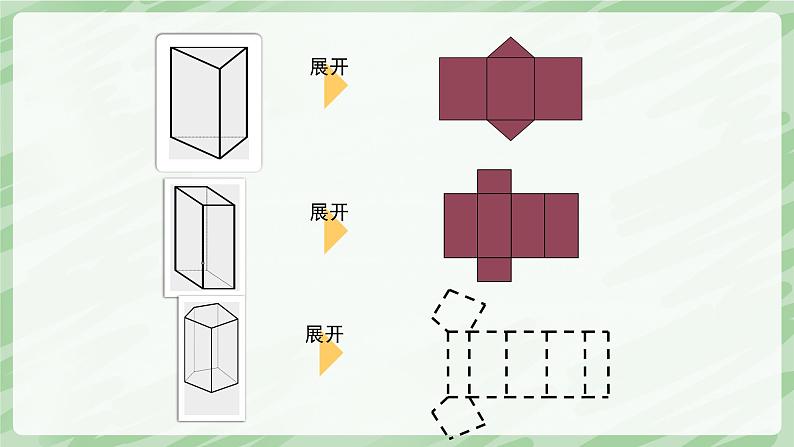
将图中的棱柱沿某些棱剪开，展开成一个平面图形，你能得到哪些形状的展开图？与同伴进行交流。
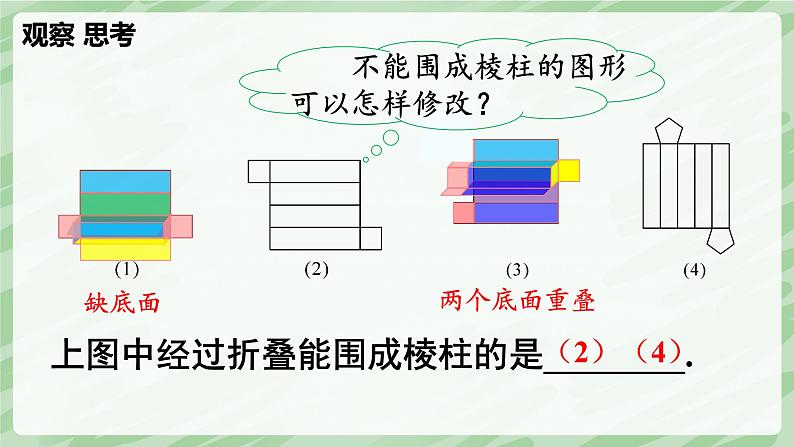
上图中经过折叠能围成棱柱的是________.
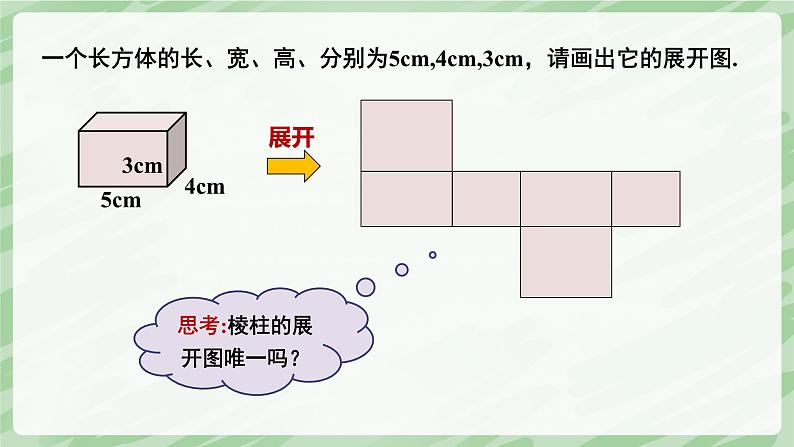
一个长方体的长、宽、高、分别为5cm,4cm,3cm，请画出它的展开图.
思考:棱柱的展开图唯一吗？
(1)棱柱的表面展开图是由两个相同的多边形和一些长方形组成的．(2)棱柱的展开图中上、下底面的边数与侧面长方形的个数相等．(3)棱柱的上、下底面分别在侧面展开图的上、下两端.
在展开与折叠的活动中，你积累了哪些经验?
1.棱柱有上下两个底面，它们的形状相同.
2.棱柱侧面的形状都是平行四边形.
3.棱柱侧面的个数和底面图形的边数相等.
4.棱柱所有侧棱长都相等.
1.如图，下列图形经过折叠不能围成一个棱柱的是(　　)
[解析]根据棱柱展开图的特点，棱柱底面边数应该和侧面数相等，因此，应选B.
将图中的棱锥沿某些棱剪开，展开成一个平面图形，你能得到哪些形状的平面图形？
（1）按照如图所示的方法把圆柱、圆锥的侧面展开，会得到什么图形？先想一想，再做一做.（2）你的想法是否正确？
2.圆柱、圆锥的展开图
如图，圆柱的侧面展开图是长方形，圆锥的侧面展开图是扇形。
想一想：圆柱和圆锥的表面展开图是什么样的呢？先想一想，再试一试.
结论：圆柱展开图是由两个等圆和一个长方形组成，其中侧面展开图的一边的长是底面圆的周长，另一边的长是圆柱的高.
圆柱展开后的平面图形是什么样的？
总结：圆锥的表面展开图是由扇形和一个圆（底面）组成，其中扇形的半径是圆锥母线（即圆锥底面圆周上任一点与顶点的连线）长，而扇形的弧长则是圆锥底面圆的周长.
圆锥展开后的平面图形是什么样的？
2.下面几个图形是一些常见几何体的展开图，你能正确说出这些几何体的名字么？
1.哪种几何体的表面能展开成下面的平面图形？先想一想，再折一折。
2．图中的两个图形经过折叠能否围成棱柱？先想一想，再折一折．
方法点拨： 由上、下底面的多边形类型可判断是几棱柱，其他类型的几何体则应记住其表面展开图的主要特征．
3.如图是立体图形的展开图，你能说出这些立体图形的名称吗？
解：(1)长方体；(2)圆锥；(3)五棱柱；(4)三棱柱．
5.如图是一种食品包装盒的表面展开图．（1）请写出这个包装盒的形状的名称：____________ ．（2）根据图中所标的尺寸，计算这个食品包装盒的表面积.
所以侧面积为3×6+5×6+4×6=18+30+24=72，底面积为 .
解： （2）因为AB=5，AD=3，BE=4，DF=6，
方法点拨：此题是将动手操作和计算相结合，了解立体图形表面展开图与立体图形间的关系，掌握图形面积的计算(公式)是解本题的关键.由表面展开图可知立体图形的表面积等于表面展开图各部分图形面积之和.
所以这个食品包装盒的表面积为72+12=84.
7.下列图形中可以作为三棱柱的展开图的是（ ）
10.小明在学习了《展开与折叠》这一课后，明白了很多几何体都能展开成平面图形．于是他在家用剪刀展开了一个长方体纸盒，可是一不小心多剪了一条棱，把纸盒剪成了两部分，即图中的①和②．根据你所学的知识，回答下列问题：（1）小明总共剪开了　 　条棱．
解：（1）由展开图发现,小明一共剪开了8条棱.
（2）现在小明想将剪断的②重新粘贴到①上去，而且经过折叠以后，仍然可以还原成一个长方体纸盒，你认为他应该将剪断的纸条粘贴到①中的什么位置？请你帮助小明在图上补全．（请在备用图中画出所有可能）
（2）如下图,四种可能
（3）小明说：他所剪的所有棱中，最长的一条棱是最短的一条棱的4倍．现在已知这个长方体纸盒的底面是一个正方形，并且这个长方体纸盒所有棱长的和是720cm，求这个长方体纸盒的体积．
（3）因为长方体纸盒的底面是一个正方形，
所以设最短的棱长即高为acm，则长与宽相等为4acm.
因为长方体纸盒所有棱长的和是720cm，
所以4(a+4a+4a)=720，解得a=20.
这长方体纸盒的体积为20×80×80=128000cm2.故答案是8;四种情况；128000 cm2.