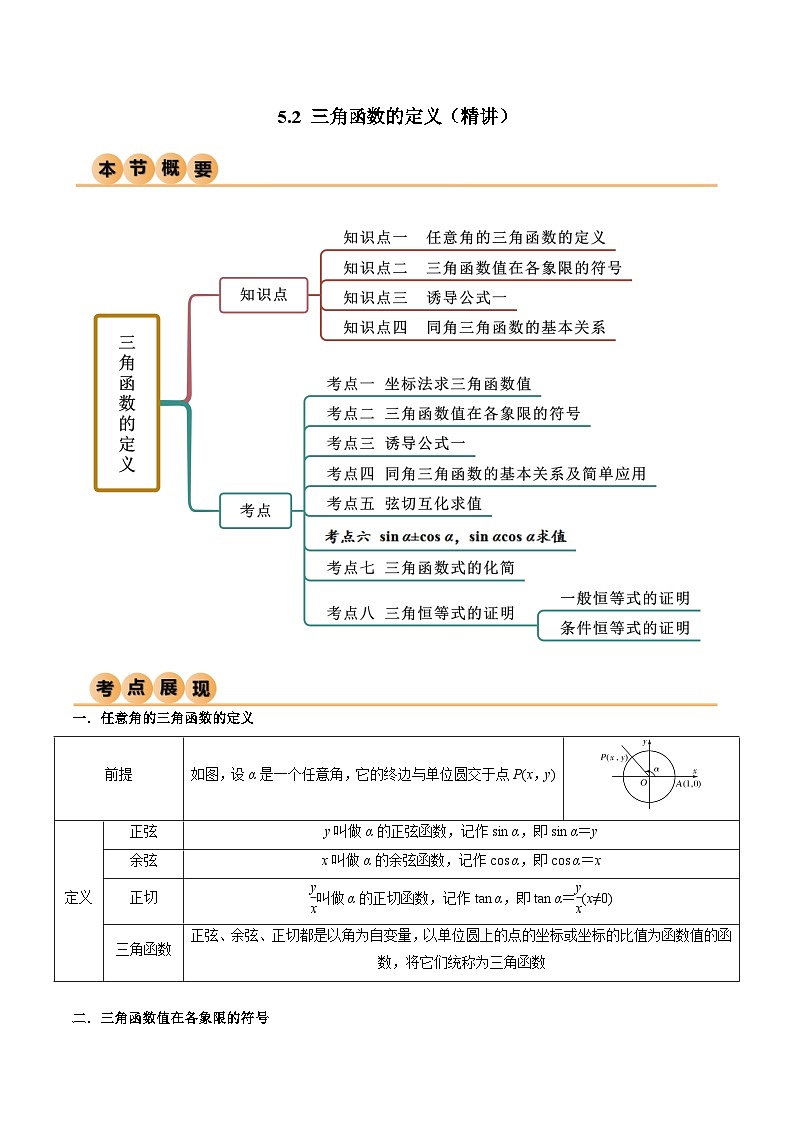




高中数学5.2.1 三角函数的概念综合训练题
展开一.任意角的三角函数的定义
二.三角函数值在各象限的符号
1.口诀概括为:一全正、二正弦、三正切、四余弦(如图).
2.根据三角函数的定义可知:
(1)正弦函数值的符号取决于纵坐标y的符号;
(2)余弦函数值的符号取决于横坐标x的符号;
(3)正切函数值的符号是由x,y的符号共同决定的,即x,y同号为正,异号为负.
三.诱导公式一
(1)语言表示:终边相同的角的同一三角函数的值相等.
(2)式子表示:eq \b\lc\{(\a\vs4\al\c1(sin(α+k·2π)=sin α,,cs(α+k·2π)=cs α,其中k∈Z.,tan(α+k·2π)=tan α,))
四.同角三角函数的基本关系
2.同角三角函数基本关系式的变形
(1)sin2α+cs2α=1⇒eq \b\lc\{(\a\vs4\al\c1(sin2α=1-cs2α,,cs2α=1-sin2α,,sin α=±\r(1-cs2α),,cs α=±\r(1-sin2α),,(sin α±cs α)2=1±2sin αcs α.))
(2)tan α=eq \f(sin α,cs α)⇒eq \b\lc\{(\a\vs4\al\c1(sin α=tan αcs α,,cs α=\f(sin α,tan α).))
一.三角函数的定义
(1)若已知角,则只需确定出该角的终边与单位圆的交点坐标,即可求出各三角函数值.
(2)若已知角α终边上一点P(x,y)(x≠0)是单位圆上一点,则sin α=y,cs α=x,tan α=eq \f(y,x).
(3)若已知角α终边上一点P(x,y)不是单位圆上一点,则先求r=eq \r(x2+y2),再求sin α=eq \f(y,r),cs α=eq \f(x,r).
(4)若已知角α终边上的点的坐标含参数,则需进行分类讨论.
二.三角函数式的化简
(1)化切为弦,即把正切函数都化为正、余弦函数,从而减少函数名称,达到化繁为简的目的.
(2)对于含有根号的,常把根号里面的部分化成完全平方式,然后去根号达到化简的目的.
(3)对于化简含高次的三角函数式,往往借助于因式分解,或构造sin2α+cs2α=1,以降低函数次数,达到化简的目的.
三.已知tan α的值,求关于sin α,cs α齐次式的值的方法
(1)对只含有sin α,cs α的齐次式,可根据同角三角函数的商数关系,通过除以某一齐次项,转化为只含有正切的式子,即化弦为切,整体代入.
(2)对于形如eq \f(asin α+bcs α,csin α+dcs α)或eq \f(asin2α+bsin αcs α+ccs2α,dsin2α+esin αcs α+fcs2α)的分式,分子、分母同时除以cs α,cs2α,将正、余弦转化为正切,从而求值.
(3)对于形如asin2α+bsin αcs α+ccs2α的式子,将其看成分母为1的分式,再将分母1变形为sin2α+cs2α,转化为形如eq \f(asin2α+bsin αcs α+ccs2α,sin2α+cs2α)的式子求值.
四.已知 sin α±cs α,sin αcs α求值问题
一般利用三角恒等式,采用整体代入的方法求解.涉及的三角恒等式有:
(1)(sin θ+cs θ)2=1+2sin θcs θ;
(2)(sin θ-cs θ)2=1-2sin θcs θ;
(3)(sin θ+cs θ)2+(sin θ-cs θ)2=2;
(4)(sin θ-cs θ)2=(sin θ+cs θ)2-4sin θcs θ.
上述三角恒等式告诉我们,已知sin θ+cs θ,sin θ-cs θ,sin θcs θ中的任何一个,则另两个式子的值均可求出.
五.证明三角恒等式常用的方法
(1)从左向右推导或从右向左推导,一般由繁到简;
(2)左右归一法,即证明左右两边都等于同一个式子;
(3)化异为同法,即针对题设与结论间的差异,有针对地变形,以消除差异;
(4)变更命题法,如要证明eq \f(a,b)=eq \f(c,d),可证ad=bc,或证eq \f(d,b)=eq \f(c,a)等;
(5)比较法,即设法证明“左边-右边=0”或“eq \f(左边,右边)=1”.
六.含有条件的三角恒等式证明的常用方法
(1)直推法:从条件直推到结论;
(2)代入法:将条件代入到结论中,转化为三角恒等式的证明;
(3)换元法:把条件和要证明的式子的三角函数问题转换为代数问题,利用代数即可完成证明.
考点一 坐标法求三角函数值
【例1-1】(2023春·四川眉山·高一校考期中)已知角的顶点为坐标原点,始边与轴非负半轴重合,终边经过点,则( )
A.B.C.D.
【例1-2】(2022秋·内蒙古呼伦贝尔·高一海拉尔第一中学校考期末)已知角的顶点为原点,起始边为轴非负半轴,若点是角终边上一点,且,则( )
A.B.C.D.
【例1-3】(2023秋·高一课时练习)已知角的终边上一点的坐标为,则角的最小正值为( )
A.B.
C.D.
【一隅三反】
1.(2023春·河北张家口·高一统考期中)若,且角的终边经过点,则( )
A.B.C.D.
2.(2023秋·云南大理 )已知角的终边落在直线上,则的值为( )
A.B.C.D.
3.(2023春·四川眉山·高一校考期中)(多选)已知角的终边经过点,则的值可能为( )
A.B.C.D.
4(2023春·广西钦州·高一统考期末)(多选)已知角的顶点为坐标原点,始边与x轴的非负半轴重合,终边上存两点,且,则( )
A.B.
C.D.
考点二 三角函数值在各象限的符号
【例2-1】(2023·全国·高一专题练习)若且,则的终边所在象限为( )
A.第一象限B.第二象限C.第三象限D.第四象限
【例2-2】(2023秋·高一课时练习)当x为第二象限角时, ( )
A.1B.0
C.2D.-2
【例2-3】(2023春·新疆·高一八一中学校考期中)若,,则的终边在( )
A.第一、三象限
B.第二、四象限
C.第一、三象限或在x轴的非负半轴上
D.第二、四象限或在x轴上
【一隅三反】
1.(2022秋·黑龙江齐齐哈尔·高一统考期末)“且”是“为第三象限角”的( )
A.充要条件B.必要不充分条件
C.充分不必要条件D.既不充分也不必要条件
2.(2023春·贵州遵义·高一统考期中)若,,则是( )
A.第一象限角B.第二象限角
C.第三象限角D.第四象限角
3.(2023秋·广东·高一统考期末)已知为第二或第三象限角,则( )
A.B.
C.D.
考点三 诱导公式一
【例3-1】(2023秋·高一课时练习)的值为( )
A.-B.
C.-D.
【例3-2】(2023春·四川宜宾·高一校考阶段练习)( )
A.B.C.D.
【一隅三反】
1.(2023春·天津南开·高一学业考试)的值为( ).
A.1B.0C.D.不存在
2.(2023春·广东河源·高一校考阶段练习)( )
A.B.C.D.
3.(2023秋·山东菏泽·高一山东省郓城第一中学校考期末)( )
A.B.C.D.
4.(2023秋 单元测试)代数式的值为( )
A.-B.C.-D.
考点四 同角三角函数公式的简单应用
【例4-1】(2023·全国·高一课堂例题)已知是第二象限角,,则( )
A.B.C.D.
【例4-2】(2023春·云南曲靖·高一校考阶段练习)若是第四象限的角,且,则 .
【一隅三反】
1.(2023春·山东济南·高一校考阶段练习)若,且为第三象限角,则( )
A.B.C.D.
2.(2023春·四川宜宾·高一校考期中)已知 ,其中,的值为( )
A.-B.-C.D.
考点五 弦切互化求值
【例5】(2023·全国·高一课堂例题)已知,则
(1) ;
(2) ;
(3) .
【一隅三反】
1.(2022秋·黑龙江齐齐哈尔·高一统考期末)已知,则的值为 .
2.(2023春·四川自贡·高一校考期中)已知,求下列各式的值.
(1);
(2).
3.(2023春·四川达州·高一校考期中)已知
(1)求的值;
(2)求的值.
考点六 sin α±cs α,sin αcs α求值
【例6-1】(2023·全国·高一课堂例题)已知,,求下列各式的值.
(1);
(2);
(3).
【例6-2】(2023秋·高一课时练习)若,,则( )
A.B.C.D.
【一隅三反】
1.(2023春·陕西渭南·高一统考期末)已知与是方程的两个根,则实数的值为( )
A.B.C.D.
2.(2023春·江西上饶·高一上饶市第一中学校考阶段练习)(多选)已知,,则下列结论正确的是( )
A.B.
C.D.
3.(2023·全国·高一专题练习)已知.
(1)求sin θcs θ的值;
(2)求sin3θ+cs3θ的值.
考点七 三角函数式的化简
【例7】(2023·全国·高一课堂例题)化简:
(1);
(2).
【一隅三反】
1(2023·高一课时练习)若,化简:.
2.(2022秋·黑龙江哈尔滨·高一尚志市尚志中学校考阶段练习)(1)化简;
(2)化简,其中是第三象限角.
考点八 三角恒等式的证明
【例8】(2023湖南)求证:
(1);
(2);
(3).
【一隅三反】
1.(2022·全国·高一专题练习)求证:
(1)
(2)
2.(2022·全国·高一专题练习)求证:
(1)=;
(2)
3.(2023秋·高一课时练习)证明下列恒等式:
(1)
(2)
前提
如图,设α是一个任意角,它的终边与单位圆交于点P(x,y)
定义
正弦
y叫做α的正弦函数,记作sin α,即sin α=y
余弦
x叫做α的余弦函数,记作cs α,即cs α=x
正切
eq \f(y,x)叫做α的正切函数,记作tan α,即tan α=eq \f(y,x)(x≠0)
三角函数
正弦、余弦、正切都是以角为自变量,以单位圆上的点的坐标或坐标的比值为函数值的函数,将它们统称为三角函数
描述方式
基本关系
基本关系式
语言描述
平方关系
sin2α+cs2α=1
同一个角α的正弦、余弦的平方和等于1
商数关系
Tan α=eq \f(sin α,cs α)(α≠kπ+eq \f(π,2),k∈Z)
同一个角α的正弦、余弦的商等于角α的正切
高中数学人教A版 (2019)必修 第一册5.6.2 函数y=Asin(ωx +φ)的图像与性质习题: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4053136_t7/?tag_id=28" target="_blank">5.6.2 函数y=Asin(ωx +φ)的图像与性质习题</a>,文件包含人教版高中数学必修一精讲精练56函数yAsinωx+φ精讲原卷版docx、人教版高中数学必修一精讲精练56函数yAsinωx+φ精讲解析版docx等2份试卷配套教学资源,其中试卷共30页, 欢迎下载使用。
高中数学人教版第一册下册三角函数当堂检测题: 这是一份高中数学人教版第一册下册<a href="/sx/tb_c9552_t7/?tag_id=28" target="_blank">三角函数当堂检测题</a>,共13页。试卷主要包含了口诀概括为,根据三角函数的定义可知,))等内容,欢迎下载使用。
高中数学人教版第一册下册第四章 三角函数三角函数同步测试题: 这是一份高中数学人教版第一册下册<a href="/sx/tb_c9552_t7/?tag_id=28" target="_blank">第四章 三角函数三角函数同步测试题</a>,共20页。试卷主要包含了口诀概括为,根据三角函数的定义可知,))等内容,欢迎下载使用。













