河北省保定市易县2024-2025学年上学期期中考试八年级数学试题

这是一份河北省保定市易县2024-2025学年上学期期中考试八年级数学试题，文件包含河北省保定市易县2024-2025学年上学期期中考试八年级数学试题docx、八年级数学CZ31b3答案pdf等2份试卷配套教学资源，其中试卷共10页， 欢迎下载使用。


注意事项：
1.满分120分,答题时间120分钟。
2.请将各题答案填写在答题卡上。
3.本次考试设卷面分。答题时，要书写认真、工整、规范、美观。
一、选择题(本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的)
1.在一个直角三角形中，若其中一个锐角是40°，则另一个锐角是
A.70° B.50° C.30° D.10°
2.下列说法中，正确的是
A.面积相等的两个图形是全等图形 B.形状相同的两个图形是全等图形
C.周长相等的两个图形是全等图形 D.能够完全重合的两个图形是全等图形
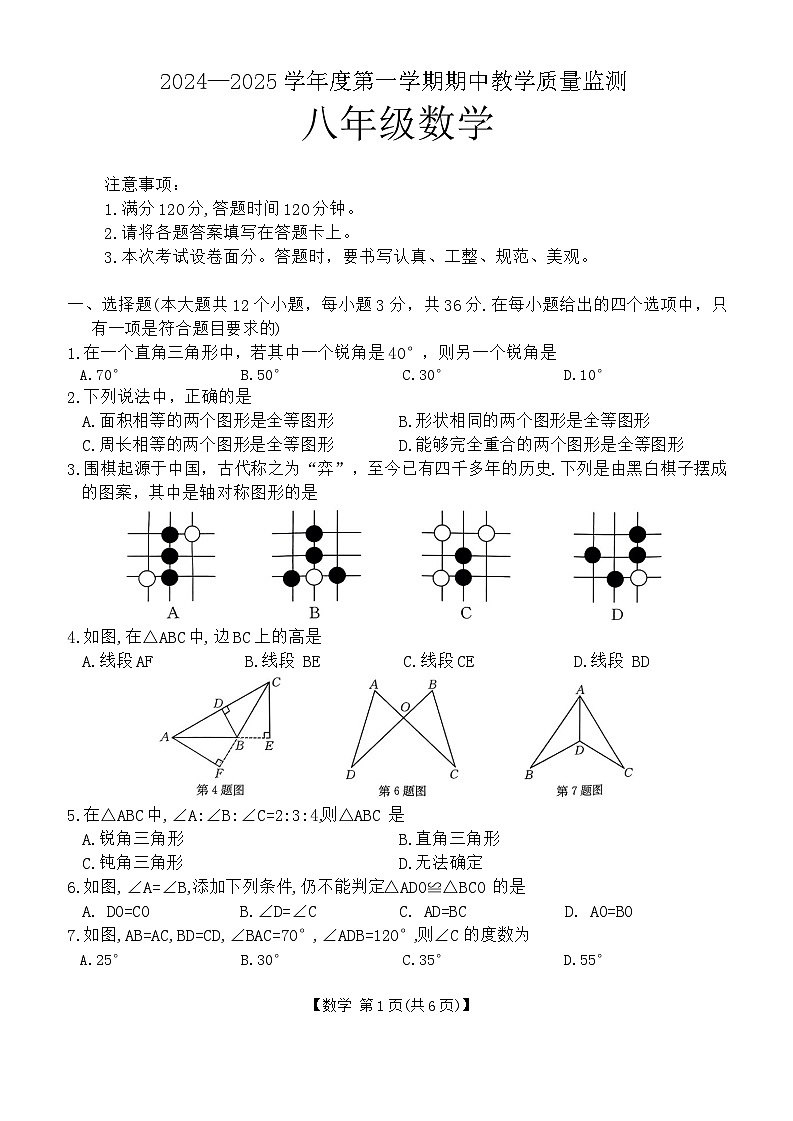
3.围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史.下列是由黑白棋子摆成的图案，其中是轴对称图形的是
4.如图,在△ABC中,边BC上的高是
A.线段AF B.线段 BE C.线段CE D.线段 BD
5.在△ABC中,∠A:∠B:∠C=2:3:4,则△ABC 是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
6.如图,∠A=∠B,添加下列条件,仍不能判定△ADO≌△BCO 的是
A. DO=CO B.∠D=∠C C. AD=BC D. AO=BO
7.如图,AB=AC,BD=CD,∠BAC=70°,∠ADB=120°,则∠C的度数为
A.25° B.30° C.35° D.55°
【数学 第1页(共6页)】 8.将一副直角三角板按照如图所示的方式摆放，则∠ABC 的度数为
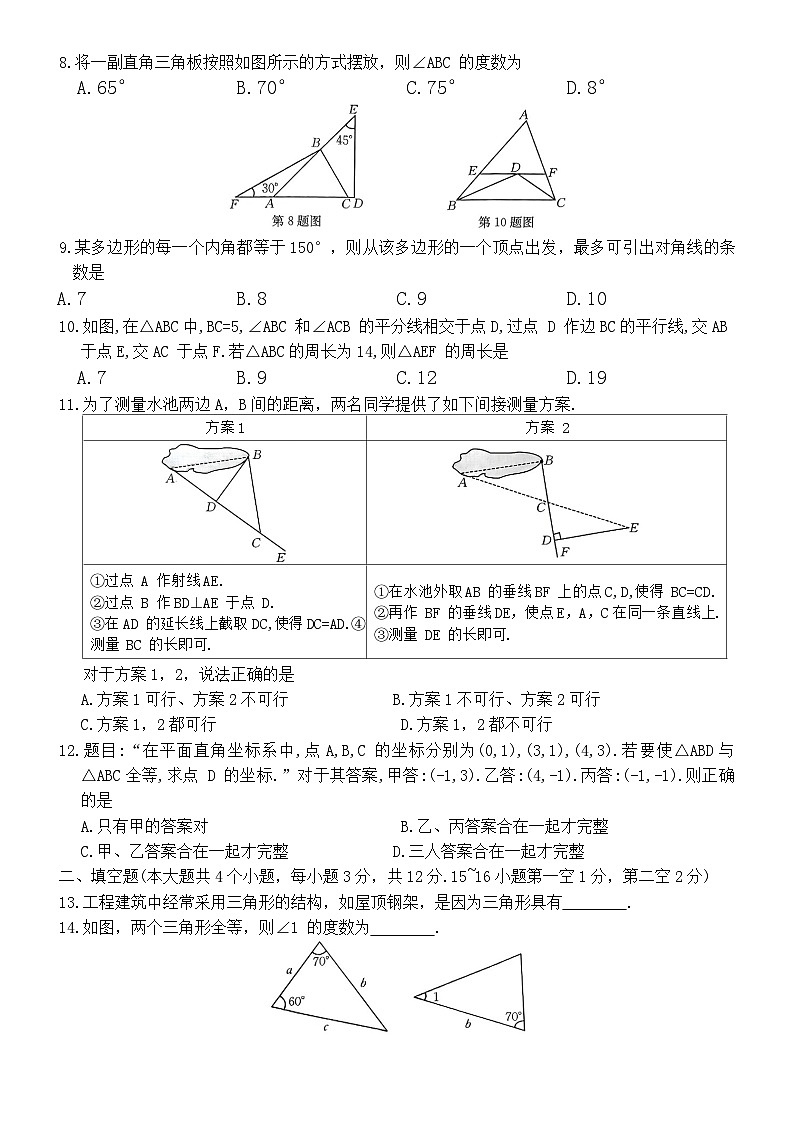
A.65° B.70° C.75° D.8°
9.某多边形的每一个内角都等于150°，则从该多边形的一个顶点出发，最多可引出对角线的条数是
A.7 B.8 C.9 D.10
10.如图,在△ABC中,BC=5,∠ABC 和∠ACB 的平分线相交于点D,过点 D 作边BC的平行线,交AB 于点E,交AC 于点F.若△ABC的周长为14,则△AEF 的周长是
A.7 B.9 C.12 D.19
11.为了测量水池两边A，B间的距离，两名同学提供了如下间接测量方案.
对于方案1，2，说法正确的是
A.方案1可行、方案2不可行 B.方案1不可行、方案2可行
C.方案1，2都可行 D.方案1，2都不可行
12.题目:“在平面直角坐标系中,点A,B,C 的坐标分别为(0,1),(3,1),(4,3).若要使△ABD与△ABC全等,求点 D 的坐标.”对于其答案,甲答:(-1,3).乙答:(4,-1).丙答:(-1,-1).则正确的是
A.只有甲的答案对 B.乙、丙答案合在一起才完整
C.甲、乙答案合在一起才完整 D.三人答案合在一起才完整
二、填空题(本大题共4个小题，每小题3分，共12分.15~16小题第一空1分，第二空2分)
13.工程建筑中经常采用三角形的结构，如屋顶钢架，是因为三角形具有 .
14.如图，两个三角形全等，则∠1 的度数为 .

【数学 第2页(共6页)】方案1
方案 2
①过点 A 作射线AE.
②过点 B 作BD⊥AE 于点 D.
③在AD 的延长线上截取DC,使得DC=AD.④测量 BC 的长即可.
①在水池外取AB 的垂线BF 上的点C,D,使得 BC=CD.
②再作 BF 的垂线DE，使点E，A，C在同一条直线上.
③测量 DE 的长即可.
15.如图,AD 是△ABC的角平分线,DE⊥AB 于点E,DE=2,AB=4.
(1)S△ABD= .
(2)若S△ABC=7,则AC 的长为 .
16.如图，∠ACF 的平分线所在的直线与∠ABC 的平分线相交于点D，与 ∠FBG的平分线相交于点E,若∠A=50°.
(1)∠D= .
(2)∠E= .
三、解答题(本大题共8小题，共72分.解答应写出文字说明、证明过程或演算步骤)
17.(本题8分)已知△ABC的三边长是a,b,c.
(1)用“>”或“<”填空:a-b+c 0,c--a-b 0,b+c-a 0.
(2)化简:|a-b+c|--|c-a-b|+|b+c-a|.
18.(本题8分)如图，在平面直角坐标系中，△ABC 的三个顶点 A−32,B−4−3,C(-1,-1).
(1)画出△ABC 关于y轴对称的△A'B'C'.
(2)在(1)的条件下，若M(x，y)是△ABC内部的任意一点，请直接写出该点在 △A'B'C'内部的对应点M'的坐标为 .
【数学 第3页(共6页)】 19.(本题8分)已知一个正多边形的边数为n.
(1)若n=6，求这个正多边形的内角和.
(2)若这个正多边形的每个内角都比与它相邻外角的3倍还多20°，求n 的值.
20.(本题8分)如图,在△ABC 和△ADE 中,AB=AD,AC=AE,∠BAD=∠CAE,DE 分别交BC,AC于点F,G,连接AF.
(1)求证:∠C=∠E.
(2)若∠GAE=24°,求∠GFC 的度数.
21.(本题8分)如图,在△ABC 中,AD 是边BC上的高,AE,BF 分别是∠BAC,∠ABC的平分线,且AE,BF 相交于点O,已知∠C=80°.
(1)求∠AOB 的度数.
(2)若∠ABC=40°,求∠DAE 的度数.
【数学 第4 页(共6页)】 22.(本题10分)如图,在△ABC中,EF垂直平分AC,交AC于点F,交BC于点E, AD⊥BC,垂足为D,且BD=DE,连接AE.
(1)求证:AB=EC.
(2)若DC+AF=16,求△ABC 的周长.
23.(本题10分)【阅读理解】
课外兴趣小组活动时，老师提出了如下问题.
如图1,在△ABC中,AB=8,AC=6,求边 BC上的中线AD 的取值范围.
小明在组内经过合作交流，得到了如下的解决方法：延长AD 到点E，使 DE=AD.
请根据小明的方法，解答下列问题.
(1)由已知和作图能得到△ADC≌△EDB 的理由是 .
A. SSS B. SAS
C. AAS D. HL
(2)AD 的取值范围是 .
A.6 C.1【感悟】
解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,在△ABC中,∠ABC=90°,BD 是斜边AC上的中线.求证: BD=12AC.
【数学 第5 页(共6页)】 24.(本题12分)(1)如图1,在△ABC 中,若AD 是边BC上的中线,则 SABDSABC=¯;如图2,在△ABC 中,若 BD=23BC,则 SABDSABC=¯.
(2)如图3,若CD,BE 分别是△ABC 的边AB,AC上的中线,求四边形 ADOE 的面积可以用如下方法.
连接AO,由AD=DB,得, SADO=SBDO,
同理，可得S△CBO=S△ABO.
设 SADO=x,SAEO=y,则 SBDO=x,SCEO=y.
设 SABC=2a,
由题意，得 SABE=12SABC=a,SADC=12SABC=a.
可列方程组 2x+y=a,x+2y=a,解得x+y= .
(3)如图4, AD=13AB,AE=23AC,若 SABC=21,求 S四边形ADOE.
【数学 第6页(共6页)】