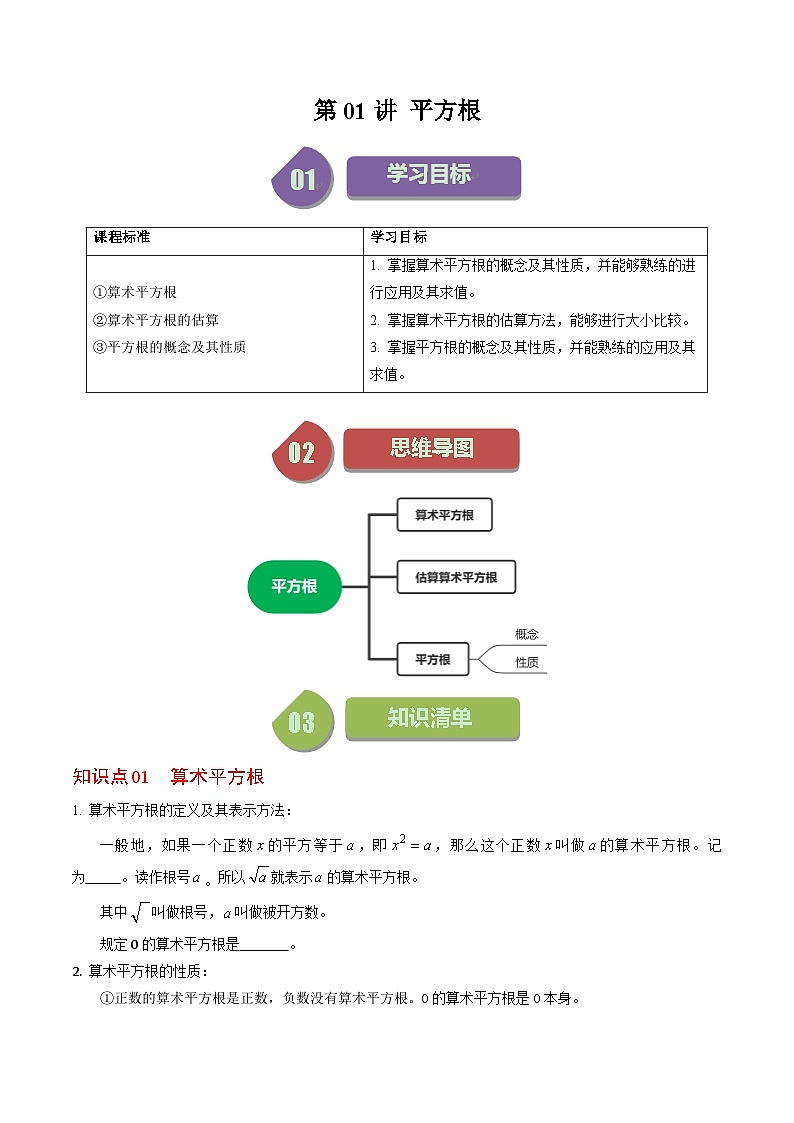
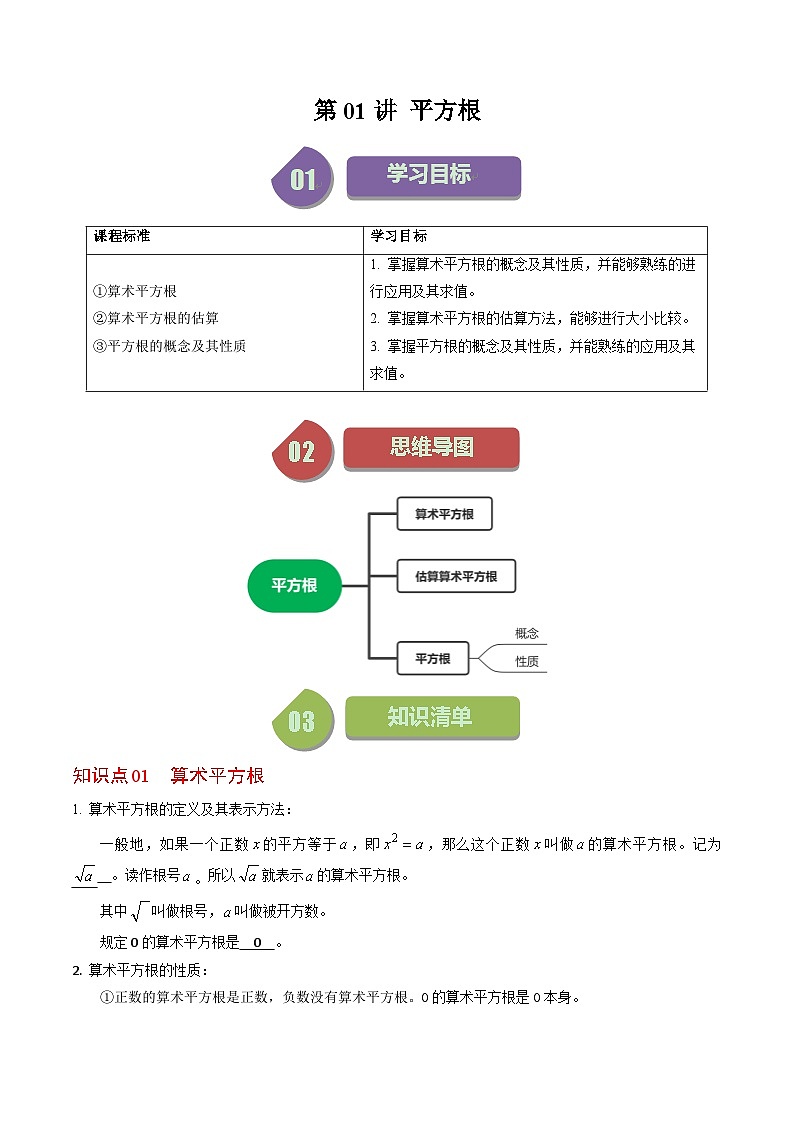
初中数学人教版（2024）七年级下册6.1 平方根优秀同步达标检测题

这是一份初中数学人教版（2024）七年级下册6.1 平方根优秀同步达标检测题，文件包含人教版数学七年级下册同步讲义+练习第六章第01讲平方根3个知识点+6类热点题型讲练+习题巩固原卷版docx、人教版数学七年级下册同步讲义+练习第六章第01讲平方根3个知识点+6类热点题型讲练+习题巩固解析版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。


知识点01 算术平方根
算术平方根的定义及其表示方法：
一般地，如果一个正数的平方等于，即，那么这个正数叫做的算术平方根。记为 。读作根号。所以就表示的算术平方根。
其中叫做根号，叫做被开方数。
规定0的算术平方根是 。
算术平方根的性质：
①正数的算术平方根是正数，负数没有算术平方根。0的算术平方根是0本身。
②算术平方根的双重非负性：
只有 才有算术平方根，且它的算术平方根也是一个 。所以算术平方根本身 ，算术平方根的被开方数也 。即 0， 0。
非负性的应用：
几个非负数的和等于0，则这几个非负数分别等于0。
即若，则 。
③一个正数的算术平方根的平方等于这个数本身。即 。
④一个数的平方的算术平方根等于这个数的绝对值。再根据这个数的正负去绝对值符号。
即 。
【即学即练1】
1．求下列各数的算术平方根．
（1）196 （2） （3）0.04 （4）102．
【即学即练2】
2．（1）＝ ，＝ ，＝ ，＝ ，＝ ，对于任意实数0，猜想＝ ．
（2）（）2＝ ，（）2＝ ，（）2＝ ，（）2＝ ，对于任意非负数a，猜想（）2＝ ．
【即学即练3】
3．如果，则＝ ．
知识点02 估算算术平方根
估算算术平方根的方法——夹逼法：
具体步骤：
①估算被开方数在那两个完全平方数之间（若一个数能被写成某个整数的平方，则称这个数为平方数）；
②确定无理数的整数步骤；
③按要求估算。
理论依据：
被开方数越大，则对应的算术平方根也越大。
【即学即练1】
4．请你估算的大小，大致范围是（ ）
A．1＜＜2B．2＜＜3C．3＜＜4D．4＜＜5
知识点03 平方根的概念与性质
平方根的概念：
如果一个数的平方等于，则这个数就叫做的 ，也叫做的二次方根。表示为 。
平方根的性质：
①正数的平方根有 个，分别是 与 ，他们互为 。
②规定0的平方根是 。所以0的平方根只有一个，就是它本身。
③负数没有平方根。
求一个数的平方根：
求一个数的平方根的运算就做开平方，与平方预算互为逆运算。
即，则。可表示为，。
【即学即练1】
5．求下列各数的平方根：
（1）121； （2）0.01； （3）； （4）（﹣13）2．
【即学即练2】
6．一个数的两个平方根分别是2a﹣1与﹣a+2，则这个数是（ ）
A．﹣1B．3C．9D．﹣3
【即学即练3】
7．求下列各式中x的值．
（1）x2﹣25＝0； （2）（x﹣1）2＝64．
题型01 求算术平方根
【典例1】实数9的算术平方根是（ ）
A．3B．±3C．D．﹣9
【变式1】的算术平方根是（ ）
A．±9B．±3C．9D．3
【变式2】求下列各式的值：
（1）； （2）； （3）．
【变式3】已知＝x，，z是9的算术平方根，求2x+y﹣z的算术平方根．
题型02 求平方根
【典例1】4的平方根是（ ）
A．﹣2B．2C．±2D．16
【变式1】（﹣9）2的平方根是（ ）
A．﹣9B．±9C．81D．
【变式2】的平方根是（ ）
A．4B．±4C．±2D．2
【变式3】求下列各数的平方根：
（1）49； （2）； （3）2； （4）0.36； （5）．
题型03 算术平方根的非负性应用
【典例1】若+＝0，则x2023+y2024的值（ ）
A．0B．1C．﹣1D．2
【变式1】已知|a﹣1|+＝0，则a+b的值为（ ）
A．﹣4B．﹣2C．2D．4
【变式2】若实数x、y满足+（y﹣3）2＝0，则等于（ ）
A．0B．5C．4D．±4
【变式3】若实数x，y满足|x﹣3|+＝0，则（x+y）3的平方根为（ ）
A．4B．8C．±4D．±8
【变式4】+|b+2|＝0，则的值是（ ）
A．0B．2018C．﹣1D．1
题型04 算术平方根的估算
【典例1】下列整数中，与最接近的是（ ）
A．2B．3C．4D．5
【变式1】的值介于下列哪两个整数之间（ ）
A．30，35B．35，40C．40，45D．45，50
【变式2】若，则整数n的值为（ ）
A．0B．1C．﹣1D．﹣2
【变式3】如图，数轴上表示的点应在（ ）
A．线段AB上B．线段BC上C．线段CD上D．线段DE上
【变式4】实数在两个相邻的整数m与m+1之间，则整数m是（ ）
A．5B．6C．7D．8
【变式5】已知a是的整数部分，b是它的小数部分，则（﹣a）3+（b+3）2＝ ．
题型05 利用两个平方根的关系求值
【典例1】一个正数的两个平方根分别是3与a+2，则a的值为（ ）
A．1B．﹣1C．﹣3D．﹣5
【变式1】一个正数的两个平方根分别是2a﹣3和5﹣a，则这个数是（ ）
A．49B．25C．16D．7
【变式2】若一个正数的平方根是2a﹣5和a+2，则a＝ ，这个正数是 ．
【变式3】若＝2，正数b的两个平方根分别是2c﹣1和﹣c+2，求2a+b+c平方根．
题型06 利用求平方根解方程
【典例1】解方程：
（1）16x2＝49； （2）（x﹣2）2＝64．
【变式1】求下列各式中x的值：
（1）9x2﹣25＝0； （2）4（2x﹣1）2＝36．
【变式2】解方程：
（1）25x2﹣49＝0； （2）2（x+1）2﹣49＝1．
1．平方根等于它本身的数是（ ）
A．﹣1B．0C．1D．±1
2．下列说法正确的是（ ）
A．﹣4的平方根是±2
B．﹣4的算术平方根是﹣2
C．的平方根是±4
D．0的平方根与算术平方根都是0
3．式子表示（ ）
A．﹣3的算术平方根B．6的算术平方根
C．9的平方根D．9的算术平方根
4．下列各式正确的是（ ）
A．＝±4B．＝﹣3C．±＝±9D．＝2
5．已知m＝20212+20222，则的值为（ ）
A．2021B．2022C．4043D．4044
6．在下列结论中，正确的是（ ）
A．B．x4的算术平方根是x2
C．﹣x2一定没有平方根D．的算术平方根是
7．已知，，则＝（ ）
A．35.12B．351.2C．111.08D．1110.8
8．一个正数的两个不同的平方根分别是2a﹣1和﹣a+2，则a为（ ）
A．0B．﹣1C．9D．1
9．，则x+y+z的值为（ ）
A．0B．1C．2D．3
10．数学实践课上，老师给同学们提供面积均为400cm2的正方形纸片，要求沿着边的方向裁出长方形．小明、小丽两位同学设计出两种裁剪方案．
小明的方案：能裁出一个长宽之比为3：2，面积为300cm2的长方形；
小丽的方案：能裁出一个长宽之比为5：3，面积为300cm2的长方形．
对于这两个方案的判断，符合实际情况的是（ ）
A．小明、小丽的方案均正确
B．小明的方案正确，小丽的方案错误
C．小明、小丽的方案均错误
D．小明的方案错误，小丽的方案正确
11．的平方根是 ．
12．已知某数的一个平方根为，则这个数的另一个平方根为 ．
13．若单项式2xmy3与3x2ym+n是同类项，则的值为 ．
14．2m﹣4和6﹣m是正数a的两个平方根，则a的值为 ．
15．已知有理数x，y，z满足，那么（x﹣yz）2的平方根为 ．
16．利用平方根求下列x的值：
（1）x2＝9； （2）（x+2）2﹣81＝0．
17．（1）已知正数x的两个平方根分别是2a﹣3和5﹣a，求a2和x的值；
（2）若＝0，求3x+6的平方根．
18．某小区准备修建一个面积为75m2的花坛，甲、乙两个工程队给出如下两个施工方案．
甲：花坛为长方形，且长与宽的比为3：1．
乙：花坛为正方形．
（1）求长方形花坛的宽．
（2）嘉淇说：“正方形花坛的边长肯定比长方形花坛的宽长3m．”请你判断嘉淇的说法是否正确，并通过计算说明．
19．【观察】|﹣2|＝2，|2|＝2；（﹣3）2＝9，32＝9．
【推理】
（1）若|x|＝1，则x＝ ；
（2）若y2＝16，则y＝ ．
【应用】
（3）已知|a+1|＝2，b2＝25．
①求a，b的值；
②若a，b同号，求a﹣b的值．
20．按要求填空：
（1）填表并观察规律：
（2）根据你发现的规律填空：
已知：＝2.638，则＝ ；
已知：＝0.06164，＝61.64，则x＝ ；
（3）从以上问题的解决过程中，你发现了什么规律，试简要说明．
课程标准
学习目标
①算术平方根
②算术平方根的估算
③平方根的概念及其性质
掌握算术平方根的概念及其性质，并能够熟练的进行应用及其求值。
掌握算术平方根的估算方法，能够进行大小比较。
掌握平方根的概念及其性质，并能熟练的应用及其求值。
a
0.0004
0.04
4
400