人教版七年级下册6.1 平方根评优课教学课件ppt

这是一份人教版七年级下册6.1 平方根评优课教学课件ppt，文件包含人教版数学七年级下册613《平方根》课件pptx、人教版数学七年级下册613《平方根》教学设计docx、人教版数学七年级下册613《平方根》导学案docx等3份课件配套教学资源，其中PPT共29页， 欢迎下载使用。

1.了解平方根的概念，并理解平方与开平方的关系;
2.会求非负数的平方根．（重点、难点）
1.什么叫一个数的算术平方根？怎样表示？
一般地，如果一个正数x的平方等于a，即 x2=a，那么这个正数x叫做a的算术平方根.
2.25的算术平方根是_____，13的算术平方根是_____.
由于(±3)2=9，所以这个数是3或-3.
与算术平方根互为相反数.
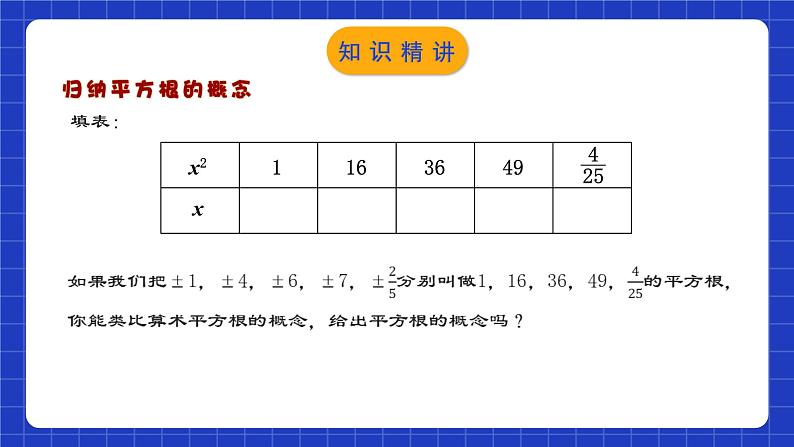
一般地，如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根. 这就是说，如果x2=a，那么x叫做a的平方根.  
例如，3和-3是9的平方根，简记为±3是9的平方根.求一个数a的平方根的运算，叫做开平方.
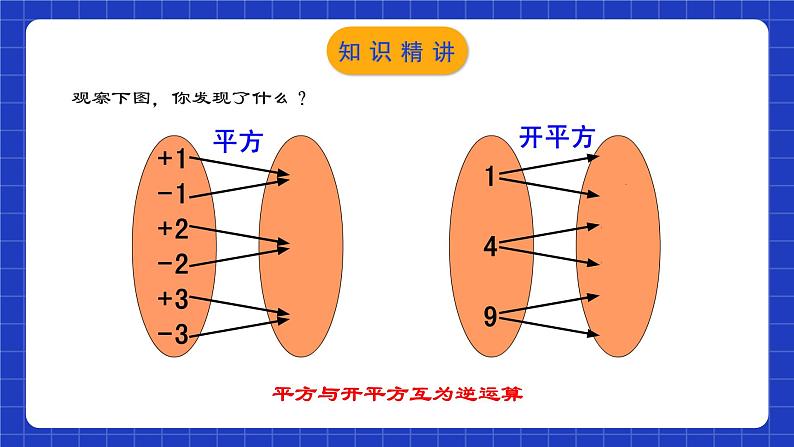
观察下图，你发现了什么？
平方与开平方互为逆运算
1.正数的平方根有什么特点？正数有两个平方根，它们互为相反数2.0的平方根是多少？0的平方根是03.负数有平方根吗？负数没有平方根
判断下列说法是否正确，并说明理由．（1）49的平方根是7； ……………………( )（2）2是4的平方根； ……………………( )（3）-5是25的平方根； ……………………( )（4）64的平方根是±8；……………………( )（5）-16的平方根是-4．……………………( )
我们已经学过一个正数的算术平方根的表示方法，你能表示一个正数的平方根吗？
例2.求下列各式的值：(1) ； (2) ； (3) .
求下列各式的值：(1) ； (2) ； (3) .
一个正数的两个平方根分别是2a＋1和a－4，求这个数．
解：由于一个正数的两个平方根是2a＋1和a－4， 则有2a＋1＋a－4＝0，即3a－3＝0，解得a＝1.所以这个数为(2a＋1)2＝(2＋1)2＝9.
1.包含关系：平方根包含算术平方根，算术平方根是平方根的一种.
平方根与算术平方根的联系与区别：
2.只有非负数才有平方根和算术平方根.
3.0的平方根是0，算术平方根也是0.
1.个数不同：一个正数有两个平方根，但只有一个算术平方根.
求一个数a的平方根的运算，叫做开平方.
1.正数有两个平方根，它们互为相反数;2.0的平方根是0;3.负数没有平方根.