新高考数学考前考点冲刺精练卷27《解三角形及其应用举例》（2份，原卷版+教师版）

这是一份新高考数学考前考点冲刺精练卷27《解三角形及其应用举例》（2份，原卷版+教师版），文件包含新高考数学考前考点冲刺精练卷27《解三角形及其应用举例》教师版doc、新高考数学考前考点冲刺精练卷27《解三角形及其应用举例》教师版pdf、新高考数学考前考点冲刺精练卷27《解三角形及其应用举例》原卷版doc、新高考数学考前考点冲刺精练卷27《解三角形及其应用举例》原卷版pdf等4份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。

一、选择题
如图，一货轮航行到M处，测得灯塔S在货轮的北偏东15°方向上，与灯塔S相距20 n mile，随后货轮按北偏西30°的方向航行30 min后，又测得灯塔在货轮的东北方向，则货轮的速度为( )
A.20(eq \r(2)＋eq \r(6))n mile/h
B.20(eq \r(6)﹣eq \r(2))n mile/h
C.20(eq \r(3)＋eq \r(6))n mile/h
D.20(eq \r(6)﹣eq \r(3))n mile/h
【答案解析】答案为：B
解析：由题意知SM＝20 n mile，∠NMS＝45°，∴SM与正东方向的夹角为75°，MN与正东方向的夹角为60°，∴∠SNM＝105°∴∠MSN＝30°，在△MNS中，利用正弦定理可得，eq \f(MN,sin 30°)＝eq \f(20,sin 105°) ，MN＝eq \f(10,\f(\r(6)＋\r(2),4))＝10(eq \r(6)﹣eq \r(2))n mile, ∴货轮航行的速度v＝20(eq \r(6)﹣eq \r(2))n mile/h.
已知A，B两地间的距离为10 km，B，C两地间的距离为20 km，现测得∠ABC＝120°，则A，C两地间的距离为( )
A.10 km B.10eq \r(3) km C.10eq \r(5) km D.10eq \r(7) km
【答案解析】答案为：D.
解析：如图所示，由余弦定理可得，AC2＝100＋400－2×10×20×cs 120°＝700，
∴AC＝10eq \r(7)(km).
一艘海轮从A处出发，以每小时40海里的速度沿南偏东40°的方向直线航行，30分钟后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是( )
A.10eq \r(2) 海里 B.10eq \r(3) 海里 C.20eq \r(3) 海里 D.20eq \r(2) 海里
【答案解析】答案为：A.
解析：画出示意图如图所示，易知，在△ABC中，AB＝20海里，∠CAB＝30°，∠ACB＝45°，根据正弦定理得eq \f(BC,sin 30°)＝eq \f(AB,sin 45°)，解得BC＝10eq \r(2)(海里).
如图，某游轮在A处看灯塔B在A的北偏东75°方向上，距离为12eq \r(6)海里，灯塔C在A的北偏西30°方向上，距离为8eq \r(3)海里，游轮由A处向正北方向航行到D处时再看灯塔B，B在南偏东60°方向上，则C与D的距离为( )
A.20海里 B.8eq \r(3) 海里 C.23eq \r(2) 海里 D.24海里
【答案解析】答案为：B.
解析：在△ABD中，因为灯塔B在A的北偏东75°方向上，距离为12eq \r(6)海里，货轮由A处向正北方向航行到D处时，再看灯塔B，B在南偏东60°方向上，所以B＝180°﹣75°﹣60°＝45°，由正弦定理eq \f(AD,sin B)＝eq \f(AB,sin∠ADB)，可得AD＝eq \f(ABsin B,sin∠ADB)＝24海里.
在△ACD中，AD＝24海里，AC＝8eq \r(3) 海里，∠CAD＝30°，
由余弦定理得CD2＝AD2＋AC2﹣2AD·ACcs 30°＝242＋(8eq \r(3))2﹣2×24×8eq \r(3)×eq \f(\r(3),2)＝192.
所以CD＝8eq \r(3) 海里.故选B.
如图，无人机在离地面高200 m的A处，观测到山顶M处的仰角为15°，山脚C处的俯角为45°，已知∠MCN＝60°，则山的高度MN为( )
A.300 m B.300eq \r(3) m C.200eq \r(3) m D.275 m
【答案解析】答案为：A
解析：∵AD∥BC，∴∠ACB＝∠DAC＝45°，∴AC＝eq \r(2)AB＝200eq \r(2)(m)，又∠MCA＝180°﹣60°﹣45°＝75°，∠MAC＝15°＋45°＝60°，∴∠AMC＝45°，在△AMC中，eq \f(MC,sin∠MAC)＝eq \f(AC,sin∠AMC)，∴MC＝eq \f(200\r(2)sin 60°,sin 45°)＝200eq \r(3) (m)，∴MN＝MCsin∠MCN＝200eq \r(3)sin 60°＝300 (m).
一艘海轮从A处出发，以40 n mile/h的速度沿南偏东40°的方向直线航行，30 min后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是( )
A.10eq \r(2) n mile B.10eq \r(3) n mile C.20eq \r(3) n mile D.20eq \r(2) n mile
【答案解析】答案为：A
解析：如图所示，
由已知条件得，∠CAB＝30°，∠ABC＝105°，∴∠BCA＝45°.又AB＝40×eq \f(1,2)＝20(n mile)，∴由正弦定理可得eq \f(AB,sin 45°)＝eq \f(BC,sin 30°)，解得BC＝10eq \r(2)(n mile).
如图，地面上四个5G中继站A，B，C，D.已知CD＝(eq \r(6)＋eq \r(2))km，∠ADB＝∠CDB＝30°，∠DCA＝45°，∠ACB＝60°，则A，B两个中继站的距离是( )
A.4eq \r(3) km B.2eq \r(10) km C.eq \r(10) km D.6eq \r(2) km
【答案解析】答案为：C.
解析：由题意可得∠DAC＝75°，∠DBC＝45°.在△ADC中，由正弦定理得AC＝eq \f(CD·sin∠ADC,sin∠DAC)＝2eq \r(3).在△BDC中，由正弦定理得BC＝eq \f(CD·sin∠BDC,sin∠DBC)＝eq \r(3)＋1.在△ACB中，由余弦定理得AB2＝AC2＋BC2﹣2×AC×BC×cs∠ACB＝(2eq \r(3))2＋(eq \r(3)＋1)2﹣2×2eq \r(3)×(eq \r(3)＋1)×eq \f(1,2)＝10，所以AB＝eq \r(10) km.
如图所示，已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与B的距离为( )
A.a km B.eq \r(3)a km C.eq \r(2)a km D.2a km
【答案解析】答案为：B；
解析：由题图可知，∠ACB=120°，由余弦定理，得AB2=AC2＋BC2－2AC·BC·cs∠ACB
=a2＋a2－2·a·a·eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))=3a2，解得AB=eq \r(3)a(km).
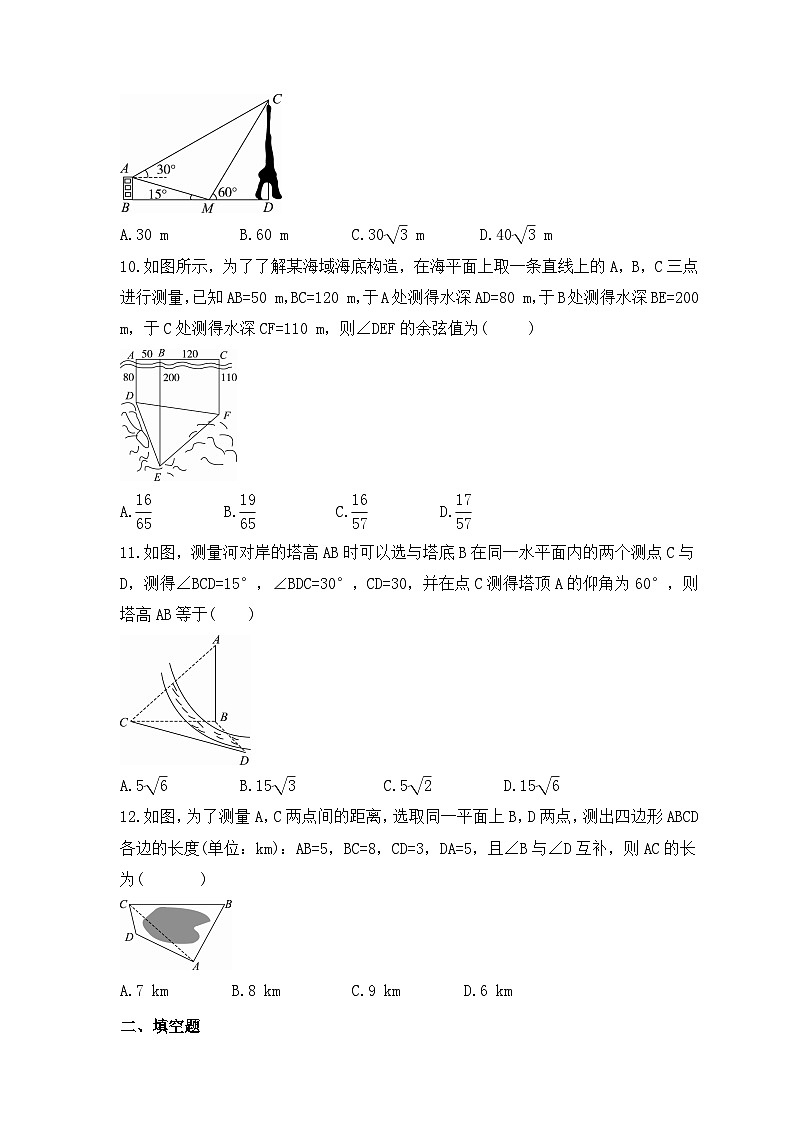
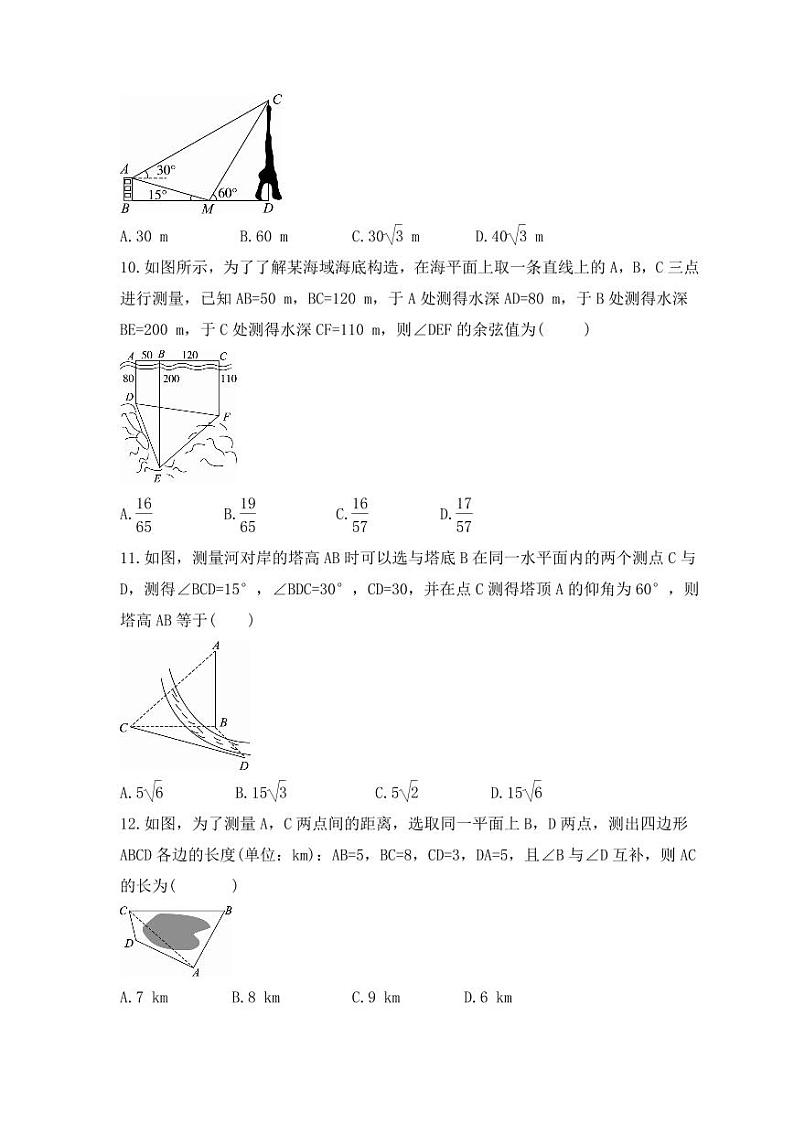
如图所示，一座建筑物AB的高为(30－10eq \r(3))m，在该建筑物的正东方向有一座通信塔CD.在它们之间的地面上的点M(B，M，D三点共线)处测得楼顶A，塔顶C的仰角分别是15°和60°，在楼顶A处测得塔顶C的仰角为30°，则通信塔CD的高为( )
A.30 m B.60 m C.30eq \r(3) m D.40eq \r(3) m
【答案解析】答案为：B；
解析：在Rt△ABM中，AM=eq \f(AB,sin∠AMB)=eq \f(30－10\r(3),sin15°)=eq \f(30－10\r(3),\f(\r(6)－\r(2),4))=20eq \r(6)(m).
过点A作AN⊥CD于点N，如图所示.易知∠MAN=∠AMB=15°，
所以∠MAC=30°＋15°=45°.
又∠AMC=180°－15°－60°=105°，所以∠ACM=30°.
在△AMC中，由正弦定理得eq \f(MC,sin45°)=eq \f(20\r(6),sin30°)，解得MC=40eq \r(3)(m).
在Rt△CMD中，CD=40eq \r(3)×sin60°=60(m)，故通信塔CD的高为60 m.
如图所示，为了了解某海域海底构造，在海平面上取一条直线上的A，B，C三点进行测量，已知AB=50 m，BC=120 m，于A处测得水深AD=80 m，于B处测得水深BE=200 m，于C处测得水深CF=110 m，则∠DEF的余弦值为( )
A.eq \f(16,65) B.eq \f(19,65) C.eq \f(16,57) D.eq \f(17,57)
【答案解析】答案为：A；
解析：如图所示，作DM∥AC交BE于N，交CF于M，
则DF=eq \r(MF2＋DM2)=eq \r(302＋1702)=10eq \r(298)(m)，DE=eq \r(DN2＋EN2)=eq \r(502＋1202)=130(m)，
EF=eq \r(BE－FC2＋BC2)=eq \r(902＋1202)=150(m).
在△DEF中，由余弦定理，得cs∠DEF=eq \f(DE2＋EF2－DF2,2DE·EF)=eq \f(1302＋1502－102×298,2×130×150)=eq \f(16,65).
如图，测量河对岸的塔高AB时可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=15°，∠BDC=30°，CD=30，并在点C测得塔顶A的仰角为60°，则塔高AB等于( )
A.5eq \r(6) B.15eq \r(3) C.5eq \r(2) D.15eq \r(6)
【答案解析】答案为：D；
解析：在△BCD中，∠CBD=180°－15°－30°=135°.
由正弦定理得eq \f(BC,sin30°)=eq \f(30,sin135°)，所以BC=15eq \r(2).
在Rt△ABC中，AB=BCtan∠ACB=15eq \r(2)×eq \r(3)=15eq \r(6).
如图，为了测量A，C两点间的距离，选取同一平面上B，D两点，测出四边形ABCD各边的长度(单位：km)：AB=5，BC=8，CD=3，DA=5，且∠B与∠D互补，则AC的长为( )
A.7 km B.8 km C.9 km D.6 km
【答案解析】答案为：D；
解析：在△ACD中，由余弦定理得：csD=eq \f(AD2＋CD2－AC2,2AD·CD)=eq \f(34－AC2,30).
在△ABC中，由余弦定理得：csB=eq \f(AB2＋BC2－AC2,2AB·BC)=eq \f(89－AC2,80).
因为∠B＋∠D=180°，所以csB＋csD=0，即eq \f(34－AC2,30)＋eq \f(89－AC2,80)=0，解得AC=7.
二、填空题
海轮“和谐号”从A处以每小时21海里的速度出发，海轮“奋斗号”在A处北偏东45°的方向，且与A相距10海里的C处，沿北偏东105°的方向以每小时9海里的速度行驶，则海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为 小时.
【答案解析】答案为：eq \f(2,3)；
解析：设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x小时，如图，
则由已知得△ABC中，AC=10，AB=21x，BC=9x，∠ACB=120°.
由余弦定理得：(21x)2=100＋(9x)2－2×10×9x×cs120°，
整理，得36x2－9x－10=0，解得x=eq \f(2,3)或x=－eq \f(5,12)(舍).
所以海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为eq \f(2,3)小时.
如图，CD是京九铁路线上的一条穿山隧道，开凿前，在CD所在水平面上的山体外取点A，B，并测得在四边形ABCD中，∠ABC＝eq \f(π,3)，∠BAD＝eq \f(2π,3)，AB＝BC＝400 m，AD＝250 m，则应开凿的隧道CD的长为________ m.
【答案解析】答案为：350.
解析：在△ABC中，因为AB＝BC＝400 m，∠ABC＝eq \f(π,3)，所以△ABC为等边三角形，即AC＝400 m，∠ACB＝eq \f(π,3).又∠BAC＝eq \f(π,3)，∠BAD＝eq \f(2π,3)，所以∠DAC＝∠BAD﹣∠BAC＝eq \f(π,3).在△ADC中，AD＝250 m，AC＝400 m，∠DAC＝eq \f(π,3)，由余弦定理得CD2＝AD2＋AC2﹣2AD·AC·cs∠DAC，即CD2＝2502＋4002﹣2×250×400×cs eq \f(π,3)，解得CD＝350 m.
如图，某工程中要将一长为100 m，倾斜角为75°的斜坡改造成倾斜角为30°的斜坡，并保持坡高不变，则坡底需加长 .
【答案解析】答案为：100eq \r(2).
解析：设坡底需加长x m，由正弦定理得eq \f(100,sin30°)=eq \f(x,sin45°)，解得x=100eq \r(2).
如图，为了测量两座山峰上P，Q两点之间的距离，选择山坡上一段长度为300eq \r(3) m且和P，Q两点在同一平面内的路段AB的两个端点作为观测点，现测得∠PAB=90°，∠PAQ=∠PBA=∠PBQ=60°，则P，Q两点间的距离为 m.
【答案解析】答案为：900；
解析：由已知，得∠QAB=∠PAB－∠PAQ=30°.
又∠PBA=∠PBQ=60°，∴∠AQB=30°，∴AB=BQ.
又PB为公共边，∴△PAB≌△PQB，∴PQ=PA.
在Rt△PAB中，AP=AB·tan60°=900，故PQ=900，
∴P，Q两点间的距离为900 m.
如图，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北30°的方向上，行驶600 m后到达B处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD=________m.
【答案解析】答案为：100eq \r(6).
解析：在△ABC中，∵∠BAC=30°，∠CBA=105°，∴∠ACB=45°.
又∵AB=600 m，∴由正弦定理eq \f(BC,sin∠BAC)=eq \f(AB,sin∠BCA)，得BC=300eq \r(2) m.
在Rt△BCD中，∠DBC=30°，BC=300eq \r(2) m，tan∠DBC=eq \f(DC,BC)=eq \f(\r(3),3)，∴DC=100eq \r(6) m.
如图，在四边形ABCD中，已知AD⊥CD，AD=10，AB=14，∠BDA=60°，∠BCD=135°，
则BC的长为________.
【答案解析】答案为：8eq \r(2)
解析：在△ABD中，设BD=x，则BA2=BD2＋AD2－2BD·AD·cs∠BDA，
即142=x2＋102－2·10x·cs 60°，整理得x2－10x－96=0，解得x1=16，x2=－6(舍去).
在△BCD中，由正弦定理：eq \f(BC,sin∠CDB)=eq \f(BD,sin∠BCD)，所以BC=eq \f(16,sin 135°)·sin 30°=8eq \r(2).
三、解答题
如图所示，在一条海防警戒线上的点A，B，C处各有一个水声监测点，B，C两点到点A的距离分别为20 km和50 km.某时刻，B收到发自静止目标P的一个声波信号，8 s后A，C同时接收到该声波信号，已知声波在水中的传播速度是1.5 km/s.
(1)设A到P的距离为x km，用x表示B，C到P的距离，并求x的值；
(2)求静止目标P到海防警戒线AC的距离.
【答案解析】解：(1)依题意，有PA=PC=x，PB=x－1.5×8=x－12.
在△PAB中，AB=20，cs∠PAB=eq \f(PA2＋AB2－PB2,2PA·AB)=eq \f(x2＋202－x－122,2x·20)=eq \f(3x＋32,5x).
同理，在△PAC中，AC=50，cs∠PAC=eq \f(PA2＋AC2－PC2,2PA·AC)=eq \f(x2＋502－x2,2x·50)=eq \f(25,x).
因为cs∠PAB=cs∠PAC，所以eq \f(3x＋32,5x)=eq \f(25,x)，解得x=31.
(2)作PD⊥AC于点D，在△ADP中，
由cs∠PAD=eq \f(25,31)，得sin∠PAD=eq \r(1－cs2∠PAD)=eq \f(4\r(21),31)，
所以PD=PAsin∠PAD=31×eq \f(4\r(21),31)=4eq \r(21)(km).
故静止目标P到海防警戒线AC的距离为4eq \r(21) km.
已知锐角三角形ABC的内角A，B，C的对边分别为a，b，c，
且满足cs2B－cs2C－sin2A=－sinAsinB，sin(A－B)=cs(A＋B).
(1)求角A，B，C；
(2)若a=eq \r(2)，求三角形ABC的边长b的值及三角形ABC的面积.
【答案解析】解：(1)∵cs2B－cs2C－sin2A=－sinAsinB，
∴sin2C＋sinAsinB=sin2A＋sin2B，
∴由正弦定理得c2＋ab=a2＋b2，
∴csC=eq \f(a2＋b2－c2,2ab)=eq \f(ab,2ab)=eq \f(1,2)，
∵0∵sin(A－B)=cs(A＋B)，
∴sinAcsB－csAsinB=csAcsB－sinAsinB，
∴sinA(sinB＋csB)=csA(sinB＋csB)，∴sinA=csA，
∴由A为锐角，可得A=eq \f(π,4)，B=π－A－C=eq \f(5π,12).
(2)∵a=eq \r(2)，A=eq \f(π,4)，B=eq \f(5π,12)，
∴由正弦定理可得b=eq \f(a·sinB,sinA)=eq \f(\r(6)＋\r(2),2)，
∴三角形ABC的面积S=eq \f(1,2)absinC=eq \f(1,2)×eq \r(2)×eq \f(\r(6)＋\r(2),2)×eq \f(\r(3),2)=eq \f(3＋\r(3),4).
在某海域A处正东方向相距80海里的B处有一艘客轮遇险，在原地等待救援.信息中心立即把消息告知在其南偏西30°，相距40海里的C处的救援船，救援船立即朝北偏东θ角的方向沿直线CB前往B处救援.
(1)若救援船的航行速度为60海里/小时，求救援船到达客轮遇险位置的时间；
(2)求tan θ的值.
【答案解析】解：(1)在题图中的△ABC中，AB=80，AC=40，∠BAC=120°，
由余弦定理可知：BC2=AB2＋AC2－2AB·AC·cs 120°，
即BC2=802＋402－2·80·40·(- eq \f(1,2))=11 200，故BC=40eq \r(7)，
故救援船到达客轮遇险位置所需时间为eq \f(40\r(7),60)=eq \f(2\r(7),3)小时.
(2)在△ABC中，由正弦定理可得eq \f(AB,sin∠ACB)=eq \f(BC,sin∠BAC)
⇒sin∠ACB=eq \f(AB,BC)sin∠BAC=eq \f(\r(21),7)，显然∠ACB为锐角，
故cs∠ACB=eq \f(2\r(7),7)，tan∠ACB=eq \f(\r(3),2)，而θ=∠ACB＋30°.
故tan θ=tan(∠ACB＋30°)=eq \f(tan∠ACB＋tan 30°,1－tan 30°tan∠ACB)=eq \f(5\r(3),3).
如图，在△ABC中，∠ABC=90°，AB=eq \r(3)，BC=1，P为△ABC内一点，∠BPC=90°.
(1)若PB=eq \f(1,2)，求PA；
(2)若∠APB=150°，求tan∠PBA.
【答案解析】解：(1)由已知得∠PBC=60°，所以∠PBA=30°.
在△PBA中，由余弦定理得PA2=3＋eq \f(1,4)－2×eq \r(3)×eq \f(1,2)cs 30°=eq \f(7,4).
故PA=eq \f(\r(7),2).
(2)设∠PBA=α，由已知得PB=sin α.
在△PBA中，由正弦定理得，eq \f(\r(3),sin 150°)=eq \f(sin α,sin30°－α)，
化简得eq \r(3)cs α=4sin α.
所以tan α=eq \f(\r(3),4)，
即tan∠PBA=eq \f(\r(3),4).