北师大版（2024）五年级上册六 组合图形的面积1 组合图形的面积练习

这是一份北师大版（2024）五年级上册六 组合图形的面积1 组合图形的面积练习，共13页。试卷主要包含了学习重难点，知识梳理，计算题，解答题等内容，欢迎下载使用。

一、学习重难点
1、学习重点：计算组合图形面积的多种方法。
2、学习难点：将组合图形转化为已经学过的基本图形。
二、知识梳理
1、求组合图形的面积。
（1）分割法求组合图形的面积;可以把组合图形分割成几个已经学过的基本图形,再把几个基本图形的面积相加。
（2）添补法求组合图形的面积:在组合图形上添上一部分,成为一个已经学过的基本图形，用基本图形的面积减去添上的图形的面积。
（3）运用组合图形的面积计算方法可以解决现实生活中组合图形的面积问题,如求正方形花坛周围的小路面积,求上面是三角形、下面是长方形的墙面面积等。
真题基础过关练
一、选择题
1．（22秋五上·辽宁·单元测试）下图的面积是（ ）cm2。（单位：cm）
A．21B．22.5
C．25D．27
2．（21秋五上·深圳·期末）下面三幅图的阴影部分面积最大的是（ ）。
A．B．C．
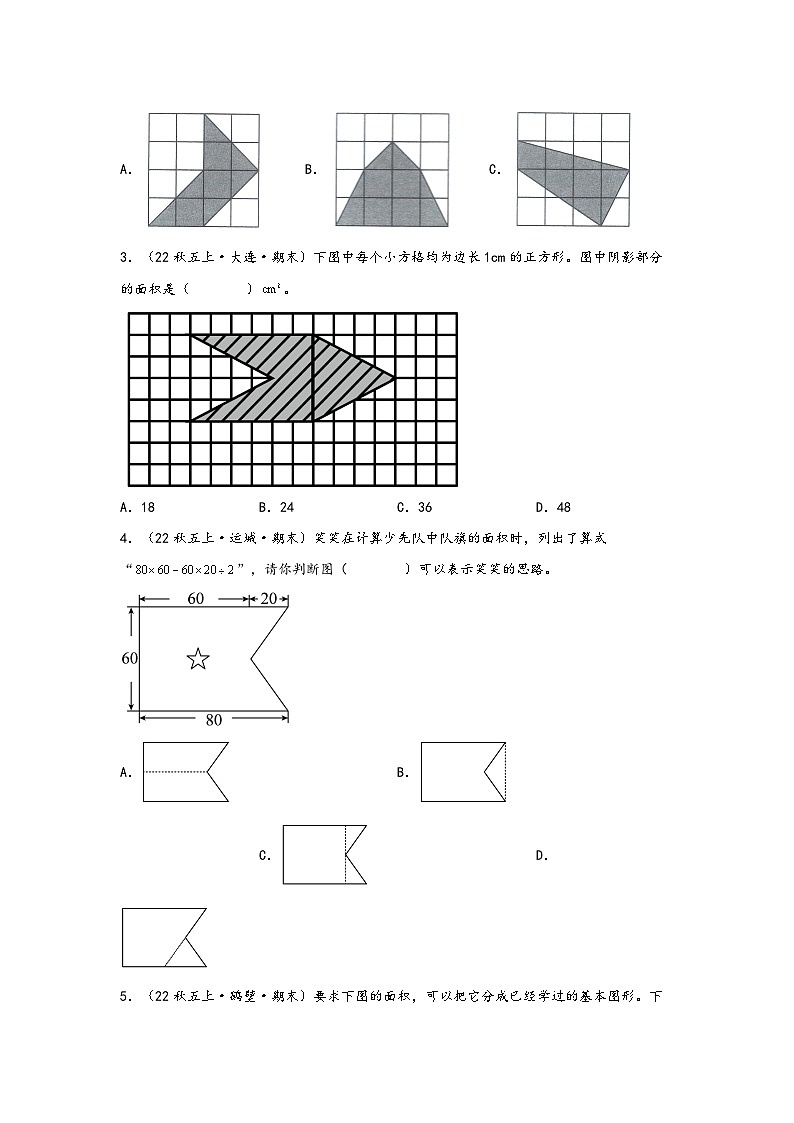
3．（22秋五上·大连·期末）下图中每个小方格均为边长1cm的正方形。图中阴影部分的面积是（ ）。
A．18B．24C．36D．48
4．（22秋五上·运城·期末）笑笑在计算少先队中队旗的面积时，列出了算式“”，请你判断图（ ）可以表示笑笑的思路。

A． B． C． D．
5．（22秋五上·鹤壁·期末）要求下图的面积，可以把它分成已经学过的基本图形。下面的分法中，不正确的是（ ）。
A．B．C．
二、填空题
6．（22秋五上·朝阳·期末）将大、小两个正方形拼在一起（如下图），大正方形的边长是小正方形边长的2倍，涂色部分的面积是( )cm2。
7．（22秋五上·常德·期末）新建某公园时，工程队计划在一块上底是40m，下底是80m，高是50m的草坪中央修建一条景观河（如图），现在草坪的面积是( )m2。
8．（21秋五上·茂名·期末）如图这个组合图形可以分成( )和( )，也可以分成( )和( )，还可以分成( )和( )。
9．（21秋五上·揭阳·期末）如图，涂色部分的面积是12平方厘米，则图中空白部分的面积是 平方厘米，平行四边形的面积是 平方厘米。
10．（22秋五上·株洲·期末）如图，钉子板上围出的多边形的面积是( )平方厘米。
三、计算题
11．（22秋五上·定西·期末）求下面图形阴影部分的面积。

真题拓展培优练
四、解答题
12．（22秋五上·郑州·期末）郑州东站地处郑州市区东部，是全国唯一个7个方向均是设计时速350千米的“米”字型高铁枢纽，同时也是一个涵盖高铁、城际、地铁、高速公路客运、城市公交、城市出租等多种交通方式的综合一体化交通枢纽。为方便旅客进出站，车站设置了很多方向指示牌。下图就是这些指示牌中的一个，根据图中的数据，算一算这个指示牌的面积有多大？
13．（22秋五上·揭阳·期末）如图，有一面墙，粉刷这面墙每平方米需用0.25千克涂料，一共要用多少千克涂料？（单位：米）
14．（22秋五上·运城·期末）24小时开放的“河东驿站”，为广大市民提供了取暖纳凉、歇脚喝水等便利服务，被誉为深夜依旧为您亮灯的“家”。下面是某驿站的平面图，请你用喜欢的方法算一算这个驿站的占地面积是多少？
参考答案
1．A
【分析】观察图形可知，组合图形的面积分为底是5cm，高是3cm的平行四边形面积与底是3cm，高是4cm的三角形面积的和；根据平行四边形面积公式：底×高；三角形面积公式：底×高÷2，代入数据，求出面积。
【详解】5×3＋3×4÷2
＝15＋12÷2
＝15＋6
＝21（cm2）
故答案为：A
【点睛】利用平行四边形面积公式和三角形面积公式进行解答，关键是熟记公式。
2．B
【分析】设每个小方格的边长为1。
A选项中图形的面积＝平行四边形的面积＋三角形的面积；
B选项中图形的面积＝梯形的面积＋三角形的面积；
C选项中图形的面积＝两个三角形的面积和。
据此分别计算出各个选项中阴影部分的面积，再比较即可求解。
【详解】由分析得：
设每个小方格的边长为1。
A．阴影部分面积为：
2×2＋2×2÷2
＝4＋4÷2
＝4＋2
＝6
B．阴影部分面积为：
（2＋4）×2÷2＋2×1÷2
＝6×2÷2＋2÷2
＝12÷2＋1
＝6＋1
＝7
C．阴影部分面积为：
4×1÷2＋4×2÷2
＝4÷2＋8÷2
＝2＋4
＝6
6＜7
阴影部分面积最大的是B选项中图形的面积。
故答案为：B
【点睛】本题主要考查了组合图形的面积，解题的关键是把不规则图形的面积转变为规则图形的面积。
3．B
【分析】根据图形的特点，可以通过平移，把右边的三角形向左平移6格，拼成一个长是6cm，宽是4cm的长方形，根据长方形的面积公式：S＝ab，把数据代入公式解答。
【详解】6×4＝24（）
下图中每个小方格均为边长1cm的正方形。图中阴影部分的面积是24cm2。
故答案为：B
【点睛】此题主要考查平移和长方形面积公式的灵活运用。
4．B
【分析】根据题意“80×60－60×20÷2”，可知，中队旗的面积等于长是80，宽60的长方形面积－底是60，高是20的三角形面积；即长方形面积－三角形面积；由此逐项分析即可解答。
【详解】A．，中队旗的面积是两个梯形面积之和，不能用“80×60－60×20÷2”解答，不符合题意；
B．，中队旗的面积是长方形面积－三角形面积，能用“80×60－60×20÷2”解答，符合题意；
C．，中队旗的面积是长方形面积＋两个三角形面积，不能用“80×60－60×20÷2”解答，不符合题意；
D．，中队旗的面积是梯形面积＋三角形面积，不能用“80×60－60×20÷2”解答；不符合题意。
笑笑在计算少先队中队旗的面积时，列出了算式“”，图可以表示笑笑的思路。
故答案为：B
【点睛】解答本题的关键是把组成图形分成哪两个规则图形，再根据规则图形的面积公式进行解答。
5．C
【分析】计算组合图形的面积，要根据已知条件对图形进行分割，转化成已学过的简单图形，先分别计算出它们的面积，再求和或差。
【详解】A．通过添加辅助线，把分割成一个梯形和一个长方形，可根据梯形、长方形面积计算公式，分别求出梯形、长方形的面积，再把它们的面积加起来。A选项正确。
B．通过添加辅助线，把分割成一个梯形和一个长方形，可根据梯形、长方形面积计算公式，分别求出梯形、长方形的面积，再把它们的面积加起来。B选项正确。
C．通过添加辅助线，把分割成一个不规则的四边形和一个三角形，不规则四边形的面积不能利用公式求出来。C选项错误。
故答案为：C
【点睛】在对组合图形进行分割时，一定要考虑到分割出来的图形是已学过的简单图形。
6．150
【分析】看图，小正方形的边长是10cm，那么大正方形的边长是20cm。涂色部分由两个三角形组成，上三角形的底是10cm，高是20cm；下三角形的底是10cm，高也是10cm。三角形面积＝底×高÷2，据此先分别求出两个三角形的面积，再相加，即可求出涂色部分的面积。
【详解】10×2＝20（cm）
（20－10）×20÷2＋10×10÷2
＝10×20÷2＋50
＝100＋50
＝150（cm2）
所以，涂色部分的面积是150cm2。
【点睛】本题考查了组合图形的面积。在计算组合图形面积时，常常将其分成几个规则图形，分别求出每个规则图形的面积后，再相加。
7．2600
【分析】从图中可知，景观河是一个底为8m，高为50m的平行四边形；则现在草坪的面积＝梯形的面积－平行四边形的面积，根据梯形的面积＝（上底＋下底）×高÷2，平行四边形的面积＝底×高，代入数据计算求解。
【详解】梯形的面积：
（40＋80）×50÷2
＝120×50÷2
＝3000（m2）
平行四边形的面积：
8×50＝400（m2）
草坪的面积：
3000－400＝2600（m2）
现在草坪的面积是2600m2。
【点睛】本题考查梯形、平行四边形面积公式的运用，分析组合图形是由哪些基本图形组成，然后看是求几种图形的面积和还是求面积差，根据图形面积公式解答。
8．正方形 梯形 三角形 梯形 长方形 三角形
【分析】用分割法可以把这个组合图形分割成几个基本图形，如下图所示。据此解答。
【详解】通过作图可知，这个组合图形可以分成正方形和梯形，也可以分成三角形和梯形，还可以分成长方形和三角形。
【点睛】把组合图形分割成学过的基本图形，是求组合图形面积的常用方法。
9．12 24
【分析】通过观察图形可知，涂色部分三角形与平行四边形等底等高，所以平行四边形的面积是涂色部分三角形面积的2倍，空白部分的面积等于涂色部分的面积。据此解答即可。
【详解】根据分析可知：
空白部分的面积＝涂色部分的面积＝12平方厘米
平行四边形面积：12×2＝24（平方厘米）
【点睛】此题考查的目的是理解掌握等底等高的平行四边形和三角形面积之间的关系及应用。
10．5.5
【分析】如下图，多边形EFCG的面积＝正方形ABCD的面积－三角形AEG的面积－三角形BFE的面积－三角形GDC的面积，正方形的面积＝边长×边长，三角形的面积＝底×高÷2，据此先求出正方形的面积，再求出3个三角形的面积，最后用正方形的面积减去3个三角形的面积即可。
【详解】3×3－2×1÷2－1×2÷2－1×3÷2
＝9－2÷2－2÷2－3÷2
＝9－1－1－1.5
＝5.5（平方厘米）
所以多边形的面积是5.5平方厘米。
【点睛】计算组合图形的面积时，可以根据图形的特点转化成已学过的图形，再利用面积公式来计算面积。
11．84cm2；22cm2
【分析】第一个阴影部分是个三角形，根据三角形面积＝底×高÷2，列式计算；
第二个阴影部分的面积＝两个正方形面积和－大三角形面积，正方形面积＝边长×边长，据此列式计算。
【详解】14×12÷2＝84（cm2）
6×6＋4×4－（6＋4）×6÷2
＝36＋16－10×6÷2
＝52－30
＝22（cm2）
12．0.95平方米
【分析】这个指示牌由一个三角形和一个长方形拼接而成，三角形面积＝底×高÷2，长方形面积＝长×宽，据此先分别求出上方三角形和下方长方形的面积，再相加，即可求出整个指示牌的面积。
【详解】1×0.4÷2＋1.5×0.5
＝0.2＋0.75
＝0.95（平方米）
答：这个指示牌的面积是0.95平方米。
【点睛】本题考查了组合图形的面积，将组合图形分割成几个常规图形，分别求面积再相加即可。
13．12千克
【分析】观察图形可知，这面墙的面积是一个长是10米，宽是4米的长方形面积，加上底是10米，高是1.6米的三角形面积，根据长方形面积公式：面积＝长×宽，三角形面积公式：面积＝底×高÷2，代入数据，求出这面墙的面积，再用这面墙的面积×0.25，即可求出一共需要涂料的数量。
【详解】（10×4＋10×1.6÷2）×0.25
＝（40＋16÷2）×0.25
＝（40＋8）×0.25
＝48×0.25
＝12（千克）
答：一共要用12千克涂料。
【点睛】本题考查组成图形的面积计算，关键是把组合图形分成规矩图形，再利用规矩图形的面积公式进行解答。
14．98平方米
【分析】如图：（分法不唯一），把图形分成一个长是8米，宽是4米的长方形和上底是8米，下底是14米，高是（10－4）米的梯形，根据长方形面积公式：面积＝长×宽；梯形面积公式：面积＝（上底＋下底）×高÷2，代入数据，即可解答。
【详解】8×4＋（8＋14）×（10－4）÷2
＝32＋22×6÷2
＝32＋132÷2
＝32＋66
＝98（平方米）
答：这个驿站的占地面积是98平方米。
【点睛】本题考查求组合图形面积，把组合图形分成规则图形，再根据规则图形的面积公式进行解答。