必修 第三册7.3.3 余弦函数的性质与图修教课内容ppt课件

这是一份必修 第三册7.3.3 余弦函数的性质与图修教课内容ppt课件，共40页。PPT课件主要包含了新知初探·自主学习，课堂探究·素养提升，kπ＋π，答案B，答案D，答案A等内容，欢迎下载使用。

【课程标准】1.借助单位圆能画出余弦函数的图象．2．了解余弦函数的周期性、单调性、奇偶性、最大 (小)值．3．借助图象理解余弦函数在[0，2π]上的性质．
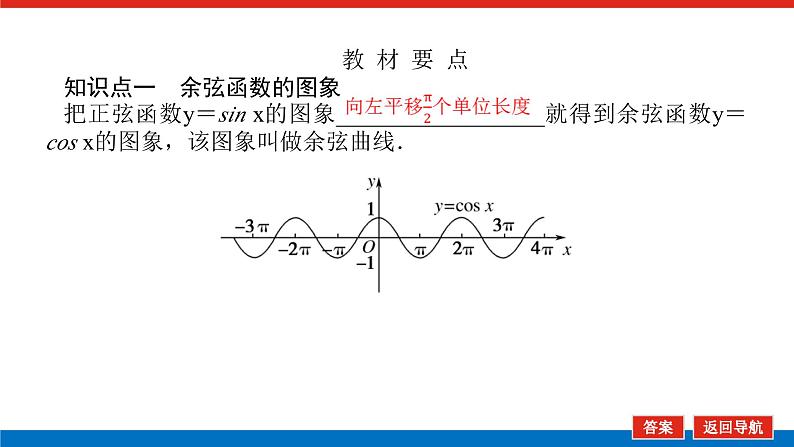
教 材 要 点知识点一　余弦函数的图象把正弦函数y＝sin x的图象__________________就得到余弦函数y＝cs x的图象，该图象叫做余弦曲线．
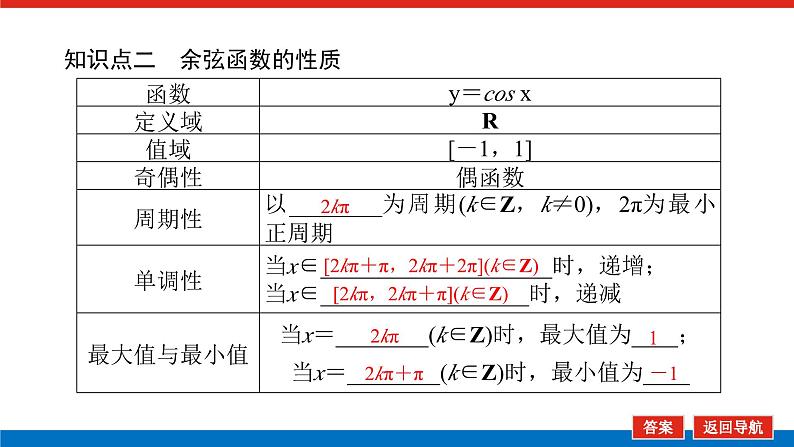
知识点二　余弦函数的性质
[2kπ＋π，2kπ＋2π](k∈Z)
[2kπ，2kπ＋π](k∈Z)
知识点三　余弦型函数y＝A cs (ωx＋φ)(x∈R)(其中A，ω，φ为常数，且A≠0，ω＞0)的周期T＝________．
2．使cs x＝1－m有意义的m的值为(　　)A．m≥0 B．0≤m≤2C．－11
解析：∵－1≤cs x≤1，∴－1≤1－m≤1，解得0≤m≤2.故选B.
课堂探究·素养提升——强化创新性题型1　用“五点法”作余弦型函数的图象例1　用“五点法”作函数y＝2＋cs x，x∈[0，2π]的简图．
在[0，2π]上找出五个关键点，用平滑的曲线连接即可．
【解析】　列表：描点连线，如图
方法归纳(1)“五点法”是作三角函数图象的常用方法，“五点”即函数图象最高点、最低点、与x轴的交点．(2)列表、描点、连线是“五点法”作图过程中的三个基本环节，注意用平滑的曲线连接五个关键点．
跟踪训练1　用“五点法”作函数y＝3－2cs x，x∈[0，2π]的简图．
解析：按五个关键点列表、描点画出图象(如图)．
状元随笔　(1)先求出函数在定义域上的单调减区间，再验证．(2)利用诱导公式化到一个单调区间，再利用单调性比较．(3)将x的系数负化正后利用单调性求解．
方法归纳1．余弦型函数单调区间的求法(1)如果x的系数为负，则利用诱导公式变为正．(2)将ωx＋φ看作整体，代入到余弦函数的单调区间解出x的范围．(3)若求具体的或一个范围内的单调区间，则给k赋值，即可求出符合条件的单调区间．2．关于三角函数值比较大小利用诱导公式，统一成正弦或余弦函数，统一化到一个单调区间内，利用单调性比较大小．
跟踪训练2　(1)将cs (－1)，cs (－2)，cs (－3)按大小顺序排列为_______________________．(用“<”连接)
解析：y＝cs x在区间(－π，0)为增函数，因为－π<－3<－2<－1<0，所以cs (－3)cs (－3)欲求函数y的最大值，须先求出a，b，为此可利用函数y 1的最大、最小值，结合分类讨论求解．
利用余弦函数的单调性求最值．
利用同角三角函数关系转化为关于余弦的二次函数求最值．
方法归纳(1)对于求形如y＝a cs x＋b的函数值域问题，一般情况下只要注意到余弦函数的性质“有界性”即可解决．注意当x有具体范围限制时，需考虑cs x的范围．(2)求解此类问题时，要先求三角函数值的范围，然后再根据其系数的正负性质求解．
方法归纳关于正、余弦函数的对称性有以下重要结论：(1)f(x)＝A sin (ωx＋φ)(或A cs (ωx＋φ))的图象关于x＝x0对称⇔f(x0)＝A或－A.(2)f(x)＝A sin (ωx＋φ)(或A cs (ωx＋φ))的图象关于点(x0，0)中心对称⇔f(x0)＝0.
教材反思(1)余弦曲线和正弦曲线的关系(2)余弦函数周期性的释疑余弦函数是周期函数，2kπ(k∈Z且k≠0)都是它的周期，最小正周期为2π.(3)余弦函数的奇偶性①余弦函数是偶函数，反映在图象上，余弦曲线关于y轴对称．②余弦曲线既是中心对称图形又是轴对称图形．
(4)余弦函数单调性的说明①余弦函数在定义域R上不是单调函数，但存在单调区间．②求解(或判断)余弦函数的单调区间(或单调性)是求值域(或最值)的关键一步．③确定含有余弦函数的较复杂的函数单调性时，要注意使用复合函数的判断方法来判断．(5)余弦函数最值的释疑①明确余弦函数的有界性，即|cs x|≤1.②对有些余弦函数，其最值不一定是1或－1，要依据函数定义域来决定．③形如y＝A cs (ωx＋φ)(A>0，ω>0)的函数的最值通常利用“整体代换”，即令ωx＋φ＝z，将函数转化为y＝A cs z的形式求最值．