高中数学沪教版（2020）选择性必修第二册8.1 成对数据的相关分析优秀课后练习题

这是一份高中数学沪教版（2020）选择性必修第二册8.1 成对数据的相关分析优秀课后练习题，文件包含沪教版2020高中数学选择性必修第二册81《成对数据的相关分析》分层练习原卷版docx、沪教版2020高中数学选择性必修第二册81《成对数据的相关分析》分层练习解析版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
一、单选题
1．（2023春·上海嘉定·高三统考阶段练习）如图是根据的观测数据得到的散点图，可以判断变量，具有线性相关关系的图是（ ）
A．①②B．③④C．②③D．①④
【答案】B
【分析】根据变量具有线性相关关系，则散点在某条直线附近，从左下至右上或从左上至右下即可.
【详解】根据变量具有线性相关关系，则散点在某条直线附近，从左下至右上或从左上至右下，
所以③④图的变量具有线性相关关系.
故选：B
2．（2023·上海·高三专题练习）通过抽样调研发现，当地第三季度的医院心脑血管疾病的人数和便利店购买冷饮的人数的相关系数很高，甲认为这是巧合，两者其实没有关系：乙认为冷饮的某种摄入成分导致了疾病；丙认为病人对冷饮会有特别需求：丁认为两者的相关关系是存在的，但不能视为因果，请判断哪位成员的意见最可能成立（ ）
A．甲B．乙C．丙D．丁
【答案】D
【分析】正确理解相关系数，相关关系与因果关系的区别是解题的关键.
【详解】当地第三季度的医院心脑血管疾病的人数和便利店购买冷饮的人数的相关系数很高，但相关关系是一种非确定性关系，相关关系不等于因果关系，丁的意见最可能成立.
故选：D.
3．（2023春·上海徐汇·高二统考阶段练习）下列关于散点图的说法中，正确的是（ ）
A．任意给定统计数据，都可以绘制散点图B．从散点图中可以看出两个量是否具有一定的关系
C．从散点图中可以看出两个量的因果关系D．从散点图中无法看出数据的分布情况
【答案】B
【分析】根据散点图的概念判断即可.
【详解】散点图不适合用于展示百分比占比的数据，另外数据量较少的数据也不适合用散点图表示，故A错误；
散点图能看出两个量是否具有一定关系，但是并一定是因果关系，故B正确，C错误；
散点图中能看出数据的分布情况，故D错误.
故选：B
4．（2023秋·上海浦东新·高二统考期末）小明同学每天阅读数学文化相关的书籍，他每天阅读的页数分别为：4、5、4.5、5、6、8、7、5、4.5、6（单位：页）.下列图形中不利于描述这些数据的是（ ）
A．条形图B．茎叶图C．散点图D．扇形图
【答案】C
【分析】根据相关图的特征理解判断.
【详解】条形图：是用宽度相同的条形的高度（或长度）表示数据的频数，故符合题意；
茎叶图：即可以保留原始数据又可以方便记录数据，故符合题意；
散点图：用两组数据构成多个坐标点，通常用于比较跨类别的成对数据，不符合题意；
扇形图：是用整个圆表示总体，用圆内各个扇形的大小表示各个部分占总体的百分数，扇形图可以容易看出各个部分所占总体的比例，故符合题意；
故选：C.
5．（2023春·高二课时练习）下列有关样本线性相关系数r的说法，错误的是（ ）
A．相关系数r可用来衡量x与y之间的线性相关程度
B．，且越接近0，相关程度越小
C．，且越接近1，相关程度越大
D．，且越接近1，相关程度越小
【答案】D
【分析】根据相关系数的定义，即可判断选项.
【详解】相关系数是来衡量两个变量之间的线性相关程度的，线性相关系数是一个绝对值小于等于1的量，并且它的绝对值越大就说明相关程度越大，所以不正确的只有D.
故选：D.
6．（2023·全国·高三专题练习）如图是根据的观测数据得到的散点图，可以判断变量具有线性相关关系的有（ ）
A．①②B．①③C．②④D．③④
【答案】D
【分析】根据散点图中各点的分布规律即可判断．
【详解】由图可知，③，④中各点比较均匀的分布在一条直线附近，具有线性相关关系．
故选：D．
7．（2023·全国·高三专题练习）某初级中学有700名学生，在2021年秋季运动会中，为响应全民健身运动的号召，要求每名学生都必须在“立定跳远”与“坐位体前屈”中选择一项参加比赛．根据报名结果知道，有的男生选择“立定跳远”，有的女生选择“坐位体前屈”，且选择“立定跳远”的学生中女生占，则参照附表，下列结论正确的是（ ）
附：
，n＝a＋b＋c＋d．A．在犯错误的概率不超过2.5%的前提下，认为选择运动项目与性别无关
B．在犯错误的概率不超过5%的前提下，认为选择运动项目与性别无关
C．有97.5%的把握认为选择运动项目与性别有关
D．有95%的把握认为选择运动项目与性别有关
【答案】C
【分析】本题利用独立性检验列表分别求出男生和女生人数后，利用相关系系数的计算公式求解即可逐项判断
【详解】解：由题意得：
设该校男生人数为x，女生人数为y，则可得如下表格：
由题意知，即，又x＋y＝700，解得则，所以有97.5%的把握认为选择运动项目与性别有关.
故选C．
8．（2023·湖南·湖南师大附中校联考模拟预测）下列关于统计概率知识的判断，正确的是（ ）
A．将总体划分为2层，通过分层随机抽样，得到两层的样本平均数和样本方差分别为和，且已知，则总体方差
B．在研究成对数据的相关关系时，相关关系越强，相关系数越接近于1
C．已知随机变量服从正态分布，若，则
D．按从小到大顺序排列的两组数据：甲组：；乙组：，若这两组数据的第30百分位数､第50百分位数都分别对应相等，则
【答案】C
【分析】对于A项，由分层抽样的方差公式判断即可；对于B项，运用越大相关性越强可判断；对于C项，由正态分布的对称性可求得结果；对于D项，运用百分位数计算公式即可求得结果.
【详解】对于A项，总体方差与样本容量有关，故A项错误；
对于B项，相关性越强，越接近于1；故B项错误；
对于C项，若，则，所以，故C项正确；
对于D项，甲组：第30百分位数为30，第50百分位数为，乙组：第30百分位数为，第50百分位数为，
所以，解得：，故.故D项错误.
故选：C.
二、填空题
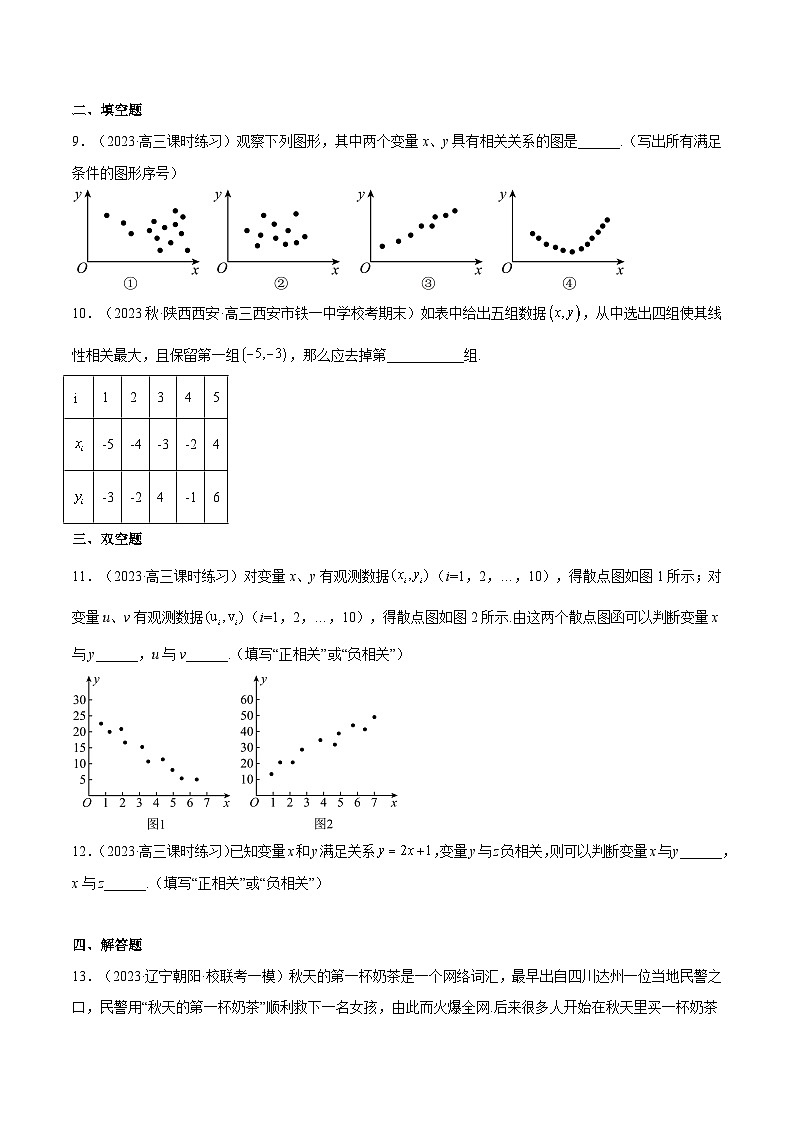
9．（2023·高三课时练习）观察下列图形，其中两个变量x、y具有相关关系的图是______.（写出所有满足条件的图形序号）
【答案】③④
【分析】根据若样本点成带状分布，则两个变量具有相关关系，结合散点图即得.
【详解】根据散点图可知在③④中，样本点成带状分布，则两个变量具有相关关系，
所以两个变量x、y具有相关关系的图是③④.
故答案为：③④.
10．（2023秋·陕西西安·高三西安市铁一中学校考期末）如表中给出五组数据，从中选出四组使其线性相关最大，且保留第一组，那么应去掉第___________组.
【答案】3
【分析】画出散点图，根据线性相关及点偏离程度判断应去掉的点.
【详解】根据表格数据，散点图如下图示：
显然偏离程度最高，故去掉第三组.
故答案为：3
三、双空题
11．（2023·高三课时练习）对变量x、y有观测数据（i=1，2，…，10），得散点图如图1所示；对变量u、v有观测数据（i=1，2，…，10），得散点图如图2所示.由这两个散点图函可以判断变量x与y______，u与v______.（填写“正相关”或“负相关”）
【答案】 负相关 正相关
【分析】根据散点图及正相关，负相关的概念即得.
【详解】由图1可知点散布在从左上角到右下角的区域，所以变量x与y负相关，
由图2可知点散布在从左下角到右上角的区域，所以变量u与v正相关.
故答案为：负相关；正相关.
12．（2023·高三课时练习）已知变量x和y满足关系，变量y与z负相关，则可以判断变量x与y______，x与z______.（填写“正相关”或“负相关”）
【答案】 正相关 负相关
【分析】根据变量之间的关系式结合相关性的概念即得.
【详解】因为变量x和y满足关系，一次项系数，
所以变量x与y正相关，
又变量y与z负相关，设，则，，
所以变量x与负相关.
故答案为：正相关；负相关.
四、解答题
13．（2023·辽宁朝阳·校联考一模）秋天的第一杯奶茶是一个网络词汇，最早出自四川达州一位当地民警之口，民警用“秋天的第一杯奶茶”顺利救下一名女孩，由此而火爆全网.后来很多人开始在秋天里买一杯奶茶送给自己在意的人.某奶茶店主记录了入秋后前7天每天售出的奶茶数量（单位：杯）
如下：
(1)请根据以上数据，绘制散点图，并根据散点图判断，与哪一个更适宜作为y关于x的回归方程模型（给出判断即可，不必说明理由）；
(2)建立y关于x的回归方程（结果保留1位小数），并根据建立的回归方程，试预测要到哪一天售出的奶茶才能超过35杯？
(3)若每天售出至少25杯即可盈利，则从第一天至第七天中任选三天，记随机变量X表示盈利的天数，求随机变量X的分布列.
参考公式和数据：其中
回归直线方程中，
【答案】(1)图见解析，更适宜作为关于的回归方程模型；
(2)，到第9天才能超过35杯；
(3)分布列见解析.
【分析】(1)根据散点图趋势即可判断；
(2)利用非线性回归方程转化为线性回归方程的方法求解；
(3)根据超几何分布求分布列.
【详解】（1）
根据散点图，知更适宜作为关于的回归方程模型；
（2）令，则，
由已知数据得，
，
所以，
故关于的回归方程为，
进而由题意知，令，整理得，即，
故当时，即到第9天才能超过35杯；
（3）由题意知，这7天中销售超过25杯的有4天，则随机变量的可能取值为
，，
，，
则随机变量的分布列为
14．（2023·全国·高三专题练习）为打造“四态融合、产村一体”的望山、见水、忆乡愁的美丽乡村，增加农民收入，某乡政府在近几年中任选了5年，经统计，年份代号x与景区农家乐接待游客人数y（单位：万人）的数据如下表：
(1)根据数据说明变量x与y是正相关还是负相关；
(2)求相关系数r的值，并说明年份与接待游客数的相关性的强与弱；
(3)分析近几年中该景区农家乐接待游客人数y的变化情况，求该景区农家乐接待游客人数关于年份代号的回归直线方程；并预测在年份代号为10时该景区农家乐接待游客的人数（单位：万人，精确到小数点后2位）.
附：一般地，当r的绝对值大于0.75时认为两个变量之间有很强的线性关系.
,
.
【答案】(1)正相关；
(2)0.959，年份与接待游客数的相关性很强；
(3)，9.04万人.
【分析】（1）根据数据结合最小二乘法可得，进而即得；
（2）根据相关系数公式结合条件即得；
（3）由题可得回归直线方程，进而即得.
【详解】（1）由表中数据可得，，
则，
由于变量y的值随x的值的增加而增加（），
因此x与y之间是正相关；
（2）因为，
所以年份与接待游客数的相关性很强；
（3）因为，
所以景区农家乐接待游客人数y关于年份代号x的回归直线方程为，
当x=10时，，
由此预测在年份代号为10时该景区农家乐接待游客人数约为9.04万人.
【能力提升】
一、填空题
1．（2023春·全国·高一专题练习）图1为某省某年1～4月份快递业务量统计图，图2为该省当年1～4月份快递业务收入统计图．
根据对以上统计图的理解，有下列四个说法：
①当年1～4月份快递业务量，3月份最高，2月份最低，差值接近2000万件；
②当年1～4月份快递业务量同比增长率均超过50%，在3月份最高，可能与春节后快递恢复网购迎来喷涨有关；
③从两图中看，快递业务量与业务收入的同比增长率并不完全一致，但业务量与业务收入变化高度一致；
④从1～4月份来看，快递业务量与快递业务收入有波动，但整体保持高速增长．
其中，正确的说法为______．（写出所有满足条件的说法序号）
【答案】①②③
【分析】①分析统计图即可得到当年1～4月份快递业务量，3月份最高，2月份最低，差值的多少.
②分析统计图即可得到当年1～4月份快递业务量同比增长率，进而得出结论.
③分析统计图即可得到快递业务量与业务收入的同比增长率是否一致，业务量与业务收入变化高度是否一致.
④分析统计图即可得到快递业务量与快递业务收入的波动情况，以及整体的变化趋势.
【详解】对于①，当年1～4月份快递业务量，3月份最高，有4397万件，2月份最低，有2411万件，其差值接近2000万件，所以①正确；
对于②，当年1～4月份快递业务量的同比增长率分别为55%，53%，62%，58%，均超过50%，在3月份最高，可能与春节后快递恢复网购迎来喷涨有关，所以②正确；
对于③，由两图易知，快递业务量与业务收入的同比增长率并不完全一致，而其业务量从高到低变化是3月→4月→1月→2月，业务收入从高到低变化也是3月→4月→1月→2月，保持高度一致，所以③正确；
对于④，由图知，快递业务收入2月对1月减少，4月对3月减少，整体不具备高速增长之说，所以④不正确．
二、解答题
2．（2022秋·上海宝山·高三上海交大附中校考阶段练习）某沙漠地区经过治理，生态系统得到很大改善，野生动物数量有所增加.为调查该地区某种野生动物的数量，将其分成面积相近的200个地块，从这些地块中用简单随机抽样的方法抽取20个作为样区，调查得到样本数据，其中和分别表示第个样区的植物覆盖面积（单位：公顷）和这种野生动物的数量（单位：头），并计算得，，，，.
(1)估计该地区这种野生动物的数量；
(2)求样本的相关系数.（精确到0.01）
【答案】(1)
(2)
【分析】（1）计算出样区野生动物的数量的平均值，乘以地块数，即得答案；
（2）根据相关系数公式进行计算，可得答案.
【详解】（1）由已知得样本平均数 ，
从而该地区这种野生动物数量的估计值为.
（2）由，，，
可得样本 的相关系数为
.
3．（2023·上海·高三专题练习）湖南省从2021年开始将全面推行“”的新高考模式，新高考对化学、生物、地理和政治等四门选考科目，制定了计算转换T分（即记入高考总分的分数）的“等级转换赋分规则”（详见附1和附2），具体的转换步骤为：①原始分Y等级转换；②原始分等级内等比例转换赋分.某校的一次年级统考中，政治、生物两选考科目的原始分分布如下表：
现从政治、生物两学科中分别随机抽取了20个原始分成绩数据，作出茎叶图：
（1）根据茎叶图，分别求出政治成绩的中位数和生物成绩的众数；
（2）该校的甲同学选考政治学科，其原始分为82分，乙同学选考生物学科，其原始分为91分，根据赋分转换公式，分别求出这两位同学的转化分；
（3）根据生物成绩在等级B的6个原始分和对应的6个转化分，得到样本数据，请计算生物原始分与生物转换分之间的相关系数，并根据这两个变量的相关系数谈谈你对新高考这种“等级转换赋分法”的看法.
附1：等级转换的等级人数占比与各等级的转换分赋分区间.
附2：计算转换分T的等比例转换赋分公式：.（其中：，，分别表示原始分Y对应等级的原始分区间下限和上限；，分别表示原始分对应等级的转换分赋分区间下限和上限.T的计算结果按四舍五入取整数）
附3：，，.
【答案】（1）政治成绩的中位数为72，生物成绩的众数为73；（2）甲、乙两位同学的转换分都为87分；（3）；答案见解析.
【解析】（1）直接观察茎叶图，由中位数和众数的概念求解.
（2）直接利用计算转换分T的等比例转换赋分公式求解.
（3）直接利用相关系数求解，利用相关关系，相关系数越接近1，相关性越强判断；也可从原始分与转化分是确定的函数关系与数据的四舍五入的误差判断.
【详解】（1）由茎叶图知：政治成绩的中位数为72，生物成绩的众数为73.
（2）甲同学选考政治学科的等级为A，
由转换赋分公式：，得.
乙同学选考生物学科的等级A，
由换赋分公式：，得.
故甲、乙两位同学的转换分都为87分.
（3）因为，，
所以.
说法1：等级转换赋分法公平，因为相关系数十分接近于1，接近于函数关系，因此高考这种“等级转换赋分法”具有公平性与合理性.
说法2：等级转换赋分法不公平.在同一等级内，原始分与转化分是确定的函数关系，理论上原始分与转化分的相关系数为1，而在实际赋分过程中由于数据的四舍五入，使得实际的转化分与应得的转化分有一定的误差，极小部分同学赋分后会出现偏高或偏低的现象.
4．（2023·广西·统考模拟预测）2016～2020年广西城乡居民人均可支配收入的柱形图如下图所示．
(1)不考虑价格因素，求广西2020年农村居民人均可支配收入的年增长率（结果精确到0.1%）．
(2)现欲了解广西各年城镇居民人均可支配收入y（单位：元）与农村居民人均可支配收入x（单位：元）是否存在较好的线性关系．设广西2016年城镇居民人均可支配收入为元，农村居民人均可支配收入为元，2017年对应的数据分别为，，2018年对应的数据分别为，，2019年对应的数据分别为，，2020年对应的数据分别为，．根据图中的五组数据，得到y关于x的线性回归方程为．试问y关于x的线性相关系数r是否大于0.95，并判断y与x之间是否存在较好的线性关系．
参考数据：，，．
附：样本的相关系数，
线性回归方程中的系数，．
【答案】(1)
(2)，y与x之间存在较好的线性关系.
【分析】（1）根据表中数据计算人均可支配收入的年增长率即可；
（2）求出，再由已知求出，根据相关系数公式求出，
【详解】（1）因为广西2020年农村居民人均可支配收入为14815元,广西2019年农村居民人均可支配收入为13676元，
所以广西2020年农村居民人均可支配收入的年增长率为.
（2）
y关于x的线性回归方程为，所以，
所以，
，
所以，
所以，
故y与x之间存在较好的线性关系.
5．（2023·全国·高三专题练习）某专营店统计了近五年来该店的创收利润y（单位：万元）与时间（单位：年）的相关数据，列表如下：
依据表中给出的数据，是否可用线性回归模型拟合y与t的关系？请计算相关系数r并加以说明（计算结果精确到0.01，若，则认为y与t高度相关，可用线性回归模型拟合y与t的关系）．
【答案】， y与t高度相关，可用线性回归模型拟合y与t的关系.
【分析】根据所给数据，由相关系数计算公式计算，即可得出结论.
【详解】由题知，，，
，，，
则，
，
y与t高度相关，可用线性回归模型拟合y与t的关系.
6．（2023·全国·高二专题练习）近年来，云南省保山市龙陵县紧紧围绕打造“中国石斛之乡”的发展定位，大力发展石斛产业，该产业带动龙陵县近四分之一人口脱贫致富．2022年8月，龙陵紫皮石斛获国家地理标志运用促进工程重点项目，并被评为优秀等次．在政府的大力扶持下，龙陵紫皮石斛产量逐年增长，2017年底到2022年底龙陵县石斛产量统计如下及散点图如图．
(1)根据散点图判断，与（a，b，c，d均为常数）哪一个更适合作为龙陵县紫皮石斛产量y关于年份代码x的回归方程类型？（给出判断即可，不必说明理由）
(2)经计算得下表中数据，根据（1）中结果，求出y关于x的回归方程；
其中．
(3)龙陵县计划到2025年底实现紫皮石斛年产量达1.5万吨，根据（2）所求得的回归方程，预测该目标是否能完成？（参考数据：）
附：，．
【答案】(1)更适合
(2)
(3)可以完成
【分析】（1）根据判断即可；
（2）根据表中数据和参考数据，利用公式求解即可；
（3）根据（2）中所得的回归方程即可预测到2025年底该目标值，从而即可判断．
【详解】（1）由散点图可知，更适合作为龙陵县紫皮石斛产量y关于年份代码x的回归方程类型．
（2）对两边取自然对数，得．
令，所以．
因为，
所以．
所以，
所以．
所以龙陵县紫皮石斛产量y关于年份代码x的回归方程为．
（3）当时，，
故预测该目标可以完成．
7．（2023·高三课时练习）某研究所将某一型号的疫苗用在小白鼠身上进行科研和临床实验，得到统计数据如下表：
现从所有试验小白鼠中任取一只，取到“注射疫苗”小白鼠的概率.
(1)求2×2列联表中的数据x、y、A、B的值；
(2)能否有99.9%的把握认为注射此种疫苗对预防R病毒有效？
附表：
【答案】(1)x=40，y=10，A=60，；
(2)有99.9%的把握认为注射此种疫苗对预防R病毒有效.
【分析】(1)由古典概型概率公式可求，再根据数据关系求；
(2)提出零假设，由公式计算的值，比较其与临界值的大小，确定是否接受假设.
【详解】（1）因为从所有试验小白鼠中任取一只，取到“注射疫苗”小白鼠的概率.
所以，所以，
所以A=100－B=60，x=60－20=40，y=40－30=10.
故；
（2）零假设为：注射疫苗与预防R病毒无关联.
因为，显然16.667>10.828，
根据小概率值的独立性检验，推断不成立，
即有99.9%的把握认为注射此种疫苗对预防R病毒有效.
8．（2023春·高二单元测试）2020年，是人类首次成功从北坡登顶珠峰60周年，也是中国首次精确测定并公布珠峰高程的45周年.华为帮助中国移动开通珠峰峰顶5G，有助于测量信号的实时开通，为珠峰高程测量提供通信保障，也验证了超高海拔地区5G信号覆盖的可能性，在持续高风速下5G信号的稳定性，在条件恶劣地区通过简易设备传输视频信号的可能性.正如任总在一次采访中所说：“华为公司价值体系的理想是为人类服务.”有人曾问，在珠峰开通5G的意义在哪里？“我认为它是科学技术的一次珠峰登顶，告诉全世界，华为5G、中国5G的底气来自哪里.现在，5G的到来给人们的生活带来更加颠覆性的变革，某IT公司基于领先技术的支持，5G经济收入在短期内逐月攀升，该IT公司在1月份至6月份的5G经济收入y（单位：百万元）关于月份x的数据如下表所示，并根据数据绘制了如图所示的散点图.
(1)根据散点图判断，与（a，b，c，d均为常数）哪一个更适宜作为5G经济收入y关于月份x的回归方程类型？（给出判断即可，不必说明理由）
(2)根据（1）的结果及表中的数据，求出y关于x的回归方程，并预测该公司7月份的5G经济收入.（结果保留小数点后两位）
(3)从前6个月的收入中抽取2个，记收入超过20百万元的个数为X，求X的分布列和数学期望.参考数据：
其中，设（i=1，2，3，4，5，6）.
参考公式：对于一组具有线性相关关系的数据（，）（i=1，2，3，…，n），其回归直线的斜率和截距的最小二乘估计公式分别为，.
【答案】(1)更适宜
(2)，65.35百万元
(3)分布列见解析，1
【分析】（1）根据散点图确定正确答案.
（2）根据非线性回归的知识求得回归方程并求得预测值.
（3）利用超几何分布的知识求得分布列并求得数学期望.
【详解】（1）根据散点图判断，更适宜作为5G经济收入y关于月份x的回归方程类型；
（2）因为，所以两边同时取常用对数，得，设，所以，因为，所以
所以.
所以，即，所以.
令，得，
故预测该公司7月份的5G经济收入大约为65.35百万元.
（3）前6个月的收入中，收入超过20百万元的有3个，所以X的取值为0，1，2，
所以X的分布列为：
所以.
9．（2023·全国·高三专题练习）为了监控某种零件的一条生产线的生产过程，检验员每隔从该生产线上随机抽取一个零件，并测量其尺寸（单位：）做好记录．下表是检验员在一天内依次抽取的个零件的尺寸：
经计算得，，，，其中为抽取的第个零件的尺寸（）．
(1)求的相关系数，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小（若，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小）；
(2)一天内抽检的零件中，如果出现了尺寸在之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．
①从这一天抽检的结果看，是否需对当天的生产过程进行检查？
②在之外的数据称为离群值，试剔除离群值，估计这条生产线当天生产的零件尺寸的均值与标准差．（精确到）
【答案】(1)；可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小
(2)①需对当天的生产过程进行检查；②均值的估计值为，标准差的估计值为．
【分析】（1）将样本数据代入相关系数公式可求得，根据可得结论；
（2）①计算出对应数据，对比样本数据即可得到结论；
②剔除出数据后，重新计算出平均数和方差，由方差和标准差关系可得标准差.
【详解】（1）由样本数据得相关系数：．
，可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小．
（2）①，，，，
抽取的第13个零件的尺寸在以外，
需对当天的生产过程进行检查．
②剔除离群值，即第个数据，剩下数据的平均数为，
即这条生产线当天生产的零件尺寸的均值的估计值为；
由得：，
剔除第个数据，剩下数据的样本方差为，
样本标准差为，
即这条生产线当天生产的零件尺寸的标准差的估计值为．
10．（2023·全国·高三专题练习）某公司为了做好产品生产计划，准确地把握市场，对过去四年的产品数据进行整理得到了第年与年销售量（单位：万件）之间的关系如下表：
(1)在图中画出表中数据的散点图；
(2)根据（1）中的散点图选择用于拟合与的回归模型，并用相关系数加以说明；
(3)建立关于的回归方程，预测第年的销售量．
（参考数据：，）
【答案】(1)散点图见解析
(2)可以用线性回归模型拟合与的关系，说明见解析
(3)回归方程为；第年销售量的预测值为万件
【分析】（1）根据表格数据直接描点即可；
（2）根据表格数据和相关系数公式可求得，由相关系数的意义可确定结论；
（3）利用最小二乘法可求得回归直线方程，代入即可得到预测值.
【详解】（1）作出散点图，如图所示，
（2）由（1）中的散点图可知，各点大致分布在一条直线附近，
根据题中所给表格及参考数据可得：，，，，，，，
；
与的相关系数近似为，说明与的线性相关程度相当强，
可以用线性回归模型拟合与的关系．
（3）设关于的回归直线方程为：，
，，
关于的回归直线方程为：，
当时，，预测第年的销售量约为万件.
11．（2023·全国·高二专题练习）经观测，某种昆虫的产卵数y与温度x有关，现将收集到的温度和产卵数（）的10组观测数据作了初步处理，得到如下图的散点图及一些统计量表．
表中，．
(1)根据散点图判断，，与哪一个适宜作为y与x之间的回归方程模型？（给出判断即可，不必说明理由）
(2)根据（1）的判断结果及表中数据，试求y关于x的回归方程．
【答案】(1)
(2)
【分析】（1）根据散点图判断，看出样本点分布在一条指数函数的周围，结合给定的回归方程模型的特征即可判断；
（2）对变换得：，变换后得样本点分布在一条直线附近，即可用线性回归方程来拟合，即可求出关于回归方程．
【详解】（1）适宜作为y与x之间的回归方程模型；
理由如下：
回归方程模型适用于散点图呈直线型；
回归方程模型适用于散点图上升，且上升趋势越来越慢；
回归方程模型适用于散点图上升，且上升趋势越来越快，呈指数型变化；
根据散点图判断，看出样本点分布在一条指数函数的周围，所以适宜作为y与x之间的回归方程模型．
（2）令，则，
由表中数据可得，；
，∴；
∴y关于x的回归方程为．
12．（2023·高二课时练习）我国西北某地区开展改造沙漠的巨大工程，该地区于2017年投入沙漠治理经费2亿元，从2018年到2020年连续3年每年增加沙漠治理经费1亿元，近4年投入的沙漠治理经费x（亿元）和沙漠治理面积y（万亩）的相关数据如下表所示：
通过绘制散点图看出，y与x之间具有明显的相关性，请用相关系数加以说明.（结果保留3位小数）
【答案】答案见解析
【分析】利用相关数据代入求出相关系数，即可得加以说明.
【详解】根据题意，得
，.
∴，
，
，
∴，
由于y与x的相关系数近似为0.998，说明y与x的线性相关程度相当高.
13．（2023·高二课时练习）假设关于某种设备的使用年限x（单位：年）与所支出的维修费用y（单位：万元）有如下统计资料：
已知，，，，.
(1)求，；
(2)计算y与x的相关系数，并判断该设备的使用年限与所支出的维修费用的相关程度.
【答案】(1)，
(2)，该设备的使用年限与所支出的维修费用之间具有很高的相关性
【分析】（1）根据平均数的计算公式即可求得答案；
（2）根据相关系数公式，即可求得相关系数，和1比较，可得出相关性的判断结果.
【详解】（1），.
（2），，
，
所以,
接近于1，说明该设备的使用年限与所支出的维修费用之间具有很高的相关性.
14．（2023春·高二课时练习）为调查野生动物保护地某种野生动物的数量，将保护地分成面积相近的300个地块，并设计两种抽样方案．
方案一：在该地区应用简单随机抽样的方法抽取30个作为样本区，依据抽样数据计算得到相应的相关系数；
方案二：在该地区应用分层抽样的方法抽取30个作为样本区，调查得到样本数据，其中和分别表示第i个样区的植物覆盖面积（单位：公顷）和这种野生动物的数量，并计算得，，，，．
(1)求该地区这种野生动物数量的估计值（这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数）；
(2)求方案二抽取的样本的相关系数r（精确到0.01），并判定哪种抽样方法更能准确地估计这种野生动物的数量．
附：若相关系数则相关性很强，的值越大相关性越强．
【答案】(1)
(2)相关系数，方案二的分层抽样方法更能准确地估计
【分析】(1)首先求出样区野生动物平均数，然后利用所求平均数乘以该地区的地块数即可求解；(2)根据所给数据以及相关系数公式即可求，然后与方案一的相关系数比较，并结合相关系数的意义即可求解.
【详解】（1）由题意可得，样区野生动物平均数为，
又因为该地区的地块数为300，
所以该地区这种野生动物的估计值为．
（2）由题中数据可得， 样本的相关系数为
．
因为方案一的相关系数为，明显小于方案二的相关系数，
所以方案二的分层抽样方法更能准确地估计．
15．（2023春·高二课时练习）某药企加大了治疗特种病的创新药的研发投入．已知市场上治疗一类慢性病的特效药品的研发费用（百万元）和销量（万盒）的统计数据如下：
(1)求与的相关系数（精确到），并判断与的关系是否可用线性回归方程模型拟合（规定时，可用线性回归方程模型拟合）；
(2)该药企准备生产药品的三类不同的剂型、、，并对其进行两次检测，当第一次检测合格后，才能进行第二次检测．第一次检测时，三类剂型、、合格的概率分别为、、；第二次检测时，三类剂型、、合格的概率分别为、、．两次检测过程相互独立．设经过两次检测后，、、三类剂型合格的种类数为，求的数学期望．
参考数据：，，．
【答案】(1)，与的关系可用线性回归模型拟合
(2)
【分析】（1）根据题意，代入相关系数计算公式，计算可得相关系数，比较得答案；
（2）分别计算三种药品剂型两次检测都合格的概率，判断经过两次检测后，、、三类剂型合格的种类数符合二项分布，代入二项分布期望计算公式，计算得答案.
【详解】（1）由题意可知，，．
由公式，．
因为，所以y与x的关系可用线性回归模型拟合；
（2）药品的每类剂型经过两次检测后合格的概率分别为：
，，．
由题意，，所以．
16．（2023春·高二课时练习）下表是弹簧伸长的长度x（cm）与拉力值y（N）的对应数据：
(1)求相关系数（保留两位小数）；
(2)通过相关系数说明y与x是否高度相关．（若，则认为y与x是高度相关的）
附：，，．
【答案】(1)
(2)y与x高度相关
【分析】(1)根据公式计算相关系数即可；
(2)根据相关系数与0.75的大小判断即可.
【详解】（1）依题意得，，
，
，
，
所以相关系数．
（2）由(1)知，，说明y与x是高度相关的．
17．（2023·高三课时练习）已知某校共有1000名学生参加体能达标测试，现从中随机抽取100名学生的成绩，将他们的测试成绩(满分：100分)分为6组：[40，50)，[50，60)，[60，70)，[70，80)，[80，90)，[90，100]，得到如下频数分布表.
（1）求这100名学生的体能测试平均成绩(同一组中的数据用该组区间的中点值为代表).
（2）在这100名学生中，规定：测试成绩不低于80分为“优秀”，成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整，并判断是否有99.9%的把握认为体能测试成绩是否优秀与性别有关？
（3）根据样本数据，可认为该校全体学生的体能测试成绩X近似服从正态分布N(μ，14.312)，其中μ近似为样本平均数，则这1000名学生中体能测试成绩不低于84.81分的估计有多少人？
参考公式及数据：X~N(μ，σ2)，P(μ-σ≤X