初中数学沪科版（2024）九年级上册23.2解直角三角形及其应用优秀课件ppt

这是一份初中数学沪科版（2024）九年级上册23.2解直角三角形及其应用优秀课件ppt，共24页。PPT课件主要包含了课件说明，两条边，acsinA，bccosA，tanA，tanB，sinA，cosB，复习旧知，新课讲解等内容，欢迎下载使用。

教学目标： 1.使学生把仰角、俯角问题转化为解直角三角形问题， 从而会把实际问题转化为数学问题来解决，进一步 提高数学建模能力； 2.通过综合运用勾股定理，直角三角形的两个锐角互 　 余及锐角三角函数解直角三角形，逐步培养学生分 　 析问题、解决问题的能力． 教学重点： 将仰角、俯角问题中的数量关系，归结为直角三角形 元素之间的关系，从而利用所学知识解决实际题．
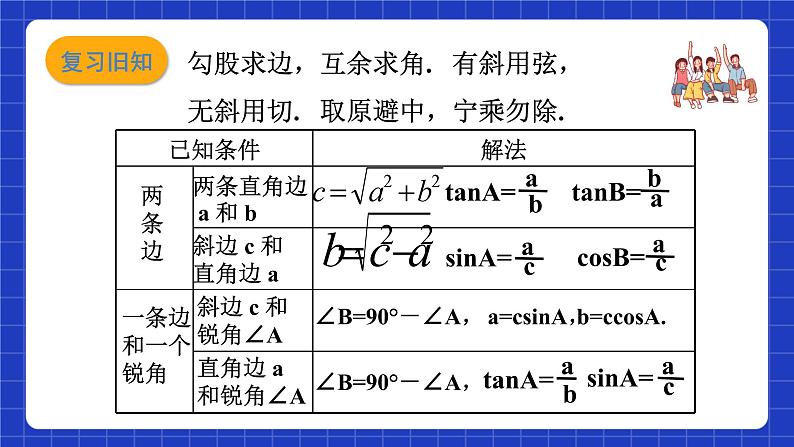
一条边和一个锐角　　　　　
斜边 c 和锐角∠A　　　　　
直角边 a 和锐角∠A　　　　　
两条直角边 a 和 b　　　　
斜边 c 和直角边 a　　　　
∠B=90°－∠A，　　　　
勾股求边，互余求角. 有斜用弦，无斜用切. 取原避中，宁乘勿除.
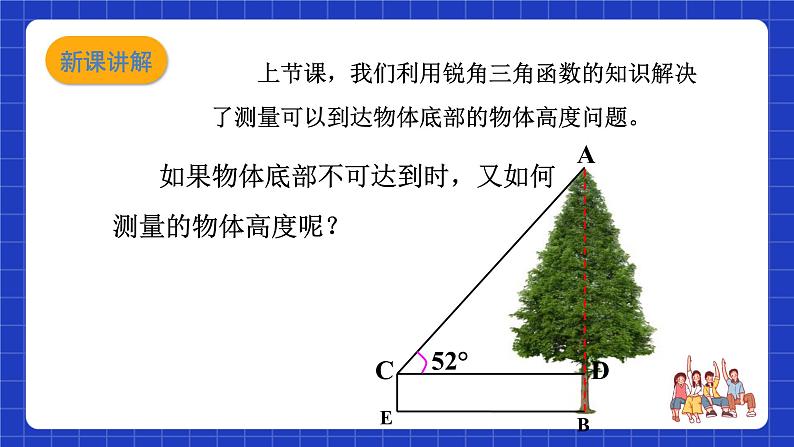
上节课，我们利用锐角三角函数的知识解决了测量可以到达物体底部的物体高度问题。
如果物体底部不可达到时，又如何测量的物体高度呢？
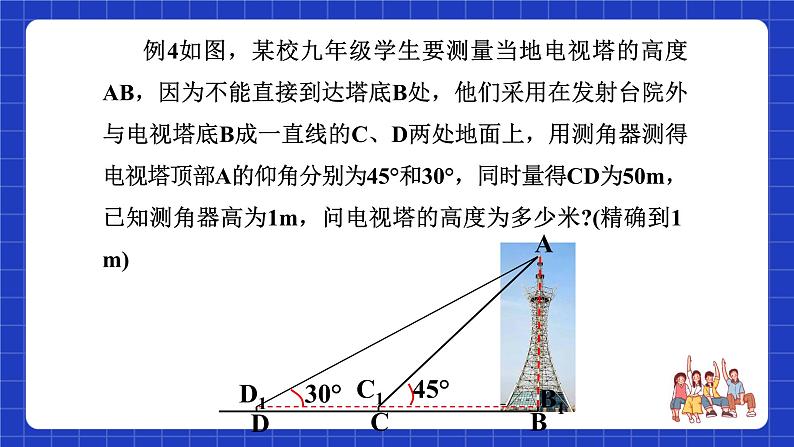
例4如图，某校九年级学生要测量当地电视塔的高度AB，因为不能直接到达塔底B处，他们采用在发射台院外与电视塔底B成一直线的C、D两处地面上，用测角器测得电视塔顶部A的仰角分别为45°和30°，同时量得CD为50m，已知测角器高为1m，问电视塔的高度为多少米?(精确到1 m)
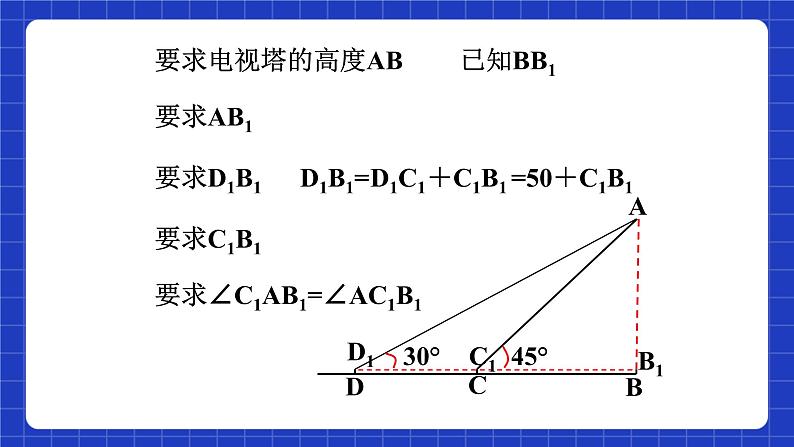
要求∠C1AB1=∠AC1B1
解:设AB1=x m. 
在Rt△AC1B1中，∵ ∠AC1B1=45°， 
∴∠C1AB1=∠AC1B1=45°，
∴C1B1=AB1. 
∵ D1C1=DC=50， 
∴D1B1=D1C1＋C1B1 
在Rt△AD1B1中，
tan∠AD1B1= 
∵ ∠AD1B1=30°， 
∴AB1=D1B1tan30°
∴x= (50＋x)
x= (50＋x)
∴3x= (50＋x)
∴3x－ =
=25( ＋1)
∴x= (50＋x)，
∴x=25( ＋1)
∴AB=AB1＋BB1 
答：电视塔的高度为69米.
∵∠AD1B1=30°， 
D1B12＋AB12 
∴(2x)2=(50＋x)2＋x2
因测量得的仰角是特殊锐角，所以可有特殊解法
∴4x2=2500＋100x＋x2＋x2
∴x2－50x－1250=0
∴2x2－100x－2500=0
∴x2－50x=1250
∴x2－50x＋625=1250＋625
∴(x－25)2=1875
∴AB1= . 
1.如图，某直升机于空中A处测得正前方地面控制点C的俯角为30°；若航向不变，直升机继续向前飞行1000米至B处，测得地面控制点C的俯角为45°.求直升机再向前飞行远，与地面控制点C的距离最近？(结果保留根号).
过点C作CD垂直于AB于D.
在Rt△BCD中，∵ ∠CBD=45°， 
∴∠BCD=∠CBD=45°，
AD=(1000＋x)m
∵∠CAD=30°， 
∴CD=ADtan30°
∴x= (1000＋x)，
∴x=500( ＋1)
2.海上有一小岛，为了测量小岛两端A、B的距离，测量人员设计了一种测量方法，如图所示，已知B点是CD的中点，E是BA延长线上的一点，测得AE=8.3海里，DE=30海里，且DE⊥EC，cs∠D= .
(1)求小岛两端A、B的距离；(2)过点C作CF⊥AB交AB的延长线于点F， 求sin∠BCF的值.
解：(1)在Rt△CDE中，
∴BE= CD
(2)在Rt△CDE中，由勾股定理得
∴cs∠BEC=cs∠BCE
∴sin∠BCF =
利用解直角三角形的知识解决实际问题的一般过程是：
　　(1)将实际问题抽象为数学问题（画出平面图形，转化为解直角三角形的问题）；　　(2)根据条件的特点，适当选用锐角三角函数等去解直角三角形；　　(3)得到数学问题的解；　　(4)得到实际问题的解．
1.如图，大楼外墙有高为AB 的广告牌，由距离大楼20 米的点 C(即CD=20米)观察它的顶部 A的仰角是55° ，底部B 的仰角是42° ．则 AB的高度为 米．参考数据：
sin55° ≈0.82，cs55° ≈0.57，tan55° ≈1.43;
sin42° ≈0.67，cs42° ≈0.74，tan42° ≈0.90.
2.如图，某景区有一处索道游览山谷的旅游点，已知索道两端距离AB为1300米，在山脚C点测得BC的距离为500米，∠ACB=90°，在C点观测山峰顶点A的仰角∠ACD=23.5°，则山峰AD的高度为 米.(参考数据:sin23.5°≈0.40,cs23.5°=0.92,tan23.5°=0.43)
3.如图，某楼房附近有一个斜坡，小张发现楼房在水平地面与斜坡处形成的投影中，在斜坡上的影子CD=6m，坡脚到楼房的距离CB＝8m.在D点处观察楼顶A点的仰角为54°，坡角∠DCE＝30º.则楼房AB的高为 m. (结果精确0.1m).( ， ， ， . )
本节课在前面研究了解直角三角形的方法，通过例3、例4介绍了利用直角三角形中余弦、正切关系解决有关测量、建筑等方面的实际问题的基础上，结合“在航海中确定轮船距离灯塔有多远”的实际问题介绍解直角三角形的理论在实际中的应用，进一步领悟解直角三角形的知识也是解决实际问题的有效数学工具，在思想和方法上是提升．