

还剩22页未读,
继续阅读
2025届重庆市江津第二中学九上数学开学达标测试试题【含答案】
展开
这是一份2025届重庆市江津第二中学九上数学开学达标测试试题【含答案】,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)已知,,,是一次函数(为常数)的图像的三点,则,,的大小关系为( )
A.B.C.D.
2、(4分)已知矩形ABCD如图,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )
A.B.C.2D.
3、(4分)要从甲、乙、丙三名学生中选出一名学生参加数学竞赛,对这三名学生进行了10次数学测试,经过数据分析,3人的平均成绩均为92分,甲的方差为0.024、乙的方差为0.08、丙的方差为0.015,则这10次测试成绩比较稳定的是( )
A.甲B.乙C.丙D.无法确定
4、(4分)下列图案中,既是轴对称图形,又是中心对称图形的是( )
A.B.C.D.
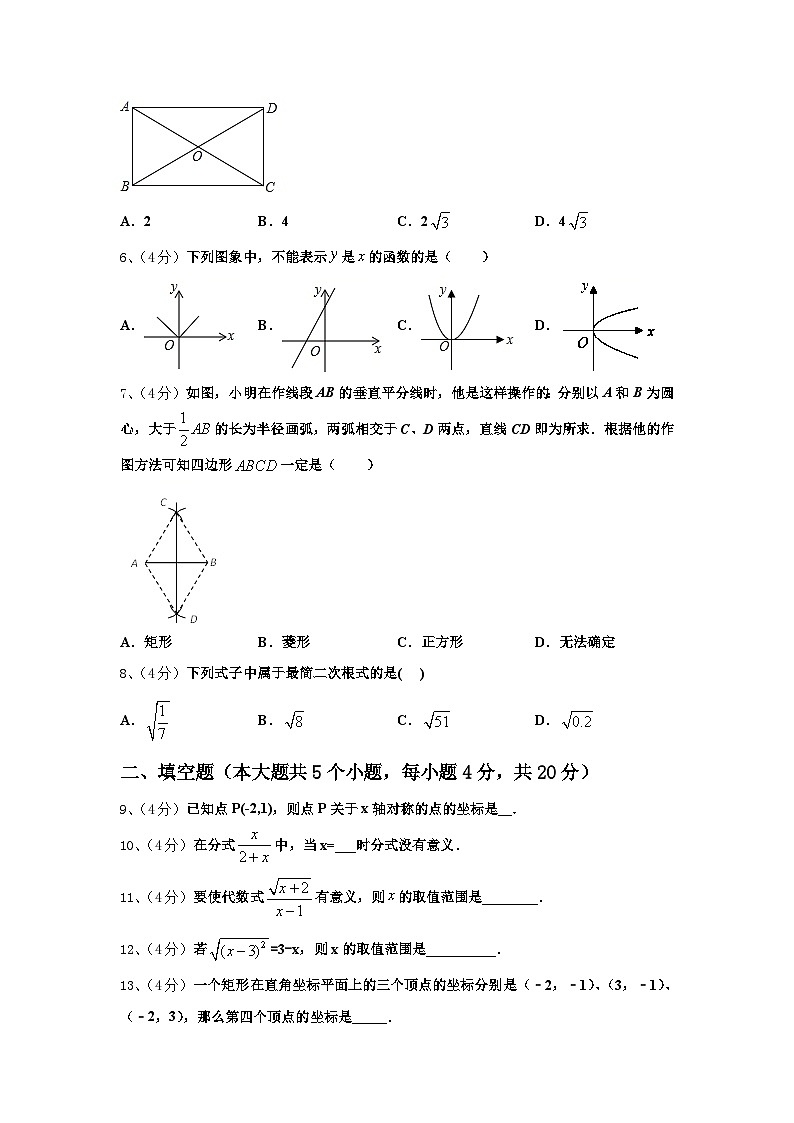
5、(4分)如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=60°,若矩形的对角线长为4,则AD的长是( )
A.2B.4C.2D.4
6、(4分)下列图象中,不能表示是的函数的是( )
A.B.C.D.
7、(4分)如图,小明在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于的长为半径画弧,两弧相交于C、D两点,直线CD即为所求.根据他的作图方法可知四边形一定是( )
A.矩形B.菱形C.正方形D.无法确定
8、(4分)下列式子中属于最简二次根式的是( )
A.B.C.D.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)已知点P(-2,1),则点P关于x轴对称的点的坐标是__.
10、(4分)在分式中,当x=___时分式没有意义.
11、(4分)要使代数式有意义,则的取值范围是________.
12、(4分)若=3-x,则x的取值范围是__________.
13、(4分)一个矩形在直角坐标平面上的三个顶点的坐标分别是(﹣2,﹣1)、(3,﹣1)、(﹣2,3),那么第四个顶点的坐标是_____.
三、解答题(本大题共5个小题,共48分)
14、(12分)在甲、乙两个不透明的口袋中装有质地、大小相同的小球,甲袋中有2个白球,1个黄球和1个红球:乙袋中装有1个白球,1个黄球和若干个红球,从乙盒中仼意摸取一球为红球的概率是从甲盒中仼意摸取一球为红球的概率的2倍.
(1)乙袋中红球的个数为 .
(2)若摸到白球记1分,摸到黄球记2分,摸到红球记0分,小明从甲、乙两袋中先后分别任意摸取一球,请用树状图或列表的方法求小明摸得两个球得2分的概率.
15、(8分)如图,在△ABC 中,AB=AC,∠BAC=120°,E 为 BC 上一点,以 CE 为直径作⊙O 恰好经过 A、C 两点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.
(1)求证:AB 是⊙O 的切线;
(2)如果 CF =2,CP =3,求⊙O 的直径 EC.
16、(8分)已知:点,.
(1)求:直线的表达式;
(2)直接写出直线向下平移2个单位后得到的直线表达式;
(3)求:在(2)的平移中直线在第三象限内扫过的图形面积.
17、(10分)点向__________平移2个单位后,所对应的点的坐标是.
18、(10分)为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打折售票,节假日按团队人数分段定价售票,即人以下(含人)的团队按原价售票;超过人的团队,其中人仍按原价售票,超过人部分的游客打折售票.设某旅游团人数为人,非节假日购票款为(元),节假日购票款为(元).与之间的函数图象如图所示.
(1)观察图象可知: ; ; ;
(2)直接写出,与之间的函数关系式;
(3)某旅行社导游王娜于5月1日带团,5月20日(非节假日)带团都到该景区旅游,共付门票款1900元,,两个团队合计50人,求,两个团队各有多少人?
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)如图,在▱ABCD中,∠ADO=30°,AB=8,点A的坐标为(﹣3,0),则点C的坐标为_____.
20、(4分)如图,正方形ABCD中,对角线AC、BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF、BF、E′F.若AE=2.则四边形ABFE′的面积是_____.
21、(4分)若关于x的一元一次不等式组的的解集为,则a的取值范围是___________.
22、(4分)下表是某校女子羽毛球队队员的年龄分布:
则该校女子排球队队员年龄的中位数为__________岁.
23、(4分)计算:π0-()-1=______.
二、解答题(本大题共3个小题,共30分)
24、(8分)如图,在平面直角坐标系中,直线与轴、轴分别交于两点,抛物线经过两点,与轴交于另一点.
(1)求抛物线解析式及点坐标;
(2)连接,求的面积;
(3)若点为抛物线上一动点,连接,当点运动到某一位置时,面积为的面积的倍,求此时点的坐标.
25、(10分)解方程:
(1)2x2﹣3x+1=1.
(2)x2﹣8x+1=1.(用配方法)
26、(12分)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、C
【解析】
先根据一次函数中k=−3判断出函数的增减性,再根据进行解答即可.
【详解】
解:∵一次函数中k=−3<0,
∴y随x的增大而减小,
∵,
∴.
故选:C.
本题考查的是一次函数图象上点的坐标特点及一次函数的性质,熟知一次函数的增减性是解答此题的关键.
2、D
【解析】
由AE平分∠BAD得∠BAE=∠DAE,根据矩形ABCD可得△ABE是等腰直角三角形,所以BE=AB=3,从而可求EC=1,连接DE,由勾股定理得DE的长,再根据三角形中位线定理可求FG的长.
【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE=3,
∵BC=AD=4,
∴EC=1,
连接DE,如图,
∴DE=,
∵点F、G分别为AD、AE的中点,
∴FG=.
故选D.
本题考查了矩形的性质以及三角形中位线定理,熟记性质与定理是解题关键.
3、C
【解析】
分析:根据方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定解答即可.
详解:因为3人的平均成绩均为92分,甲的方差为0.024、乙的方差为0.08、丙的方差为0.015,
所以这10次测试成绩比较稳定的是丙,
故选C.
点睛:本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
4、B
【解析】
根据轴对称图形与中心对称图形的概念求解.
【详解】
A.是轴对称图形,不是中心对称图形,故此选项错误;
B.是轴对称图形,也是中心对称图形,故此选项正确;
C.是轴对称图形,不是中心对称图形,因为找不到任何这样的一点,旋转180度后它的两部分能够重合,故此选项错误;
D.是轴对称图形,不是中心对称图形,故此选项错误.
故选B.
本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后两部分重合.
5、C
【解析】
根据矩形性质得出AC=2AO,BD=2BO,AC=BD=4,推出AO=OB=2,得出等边三角形AOB,可得AB=2,由勾股定理可求AD的长.
【详解】
∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD=4,
∴AO=OB=2,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,AB=2=OA
∴
故选:C.
本题考查了等边三角形的性质和判定,矩形的性质的应用,注意:矩形的对角线互相平分且相等.
6、D
【解析】
根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,可得答案.
【详解】
A、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故A不符合题意;
B、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故B不符合题意;
C、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故C不符合题意;
D、不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故D符合题意;
故选:D.
考查了函数的定义,利用了函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
7、B
【解析】
根据菱形的判定方法:四边都相等的四边形是菱形判定即可.
【详解】
根据作图方法可得:,
因此四边形ABCD一定是菱形.
故选:B
本题考查了菱形的判定,解题的关键在于根据四边相等的四边形是菱形判断.
8、C
【解析】
检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
【详解】
解:A、被开方数含分母,故A错误;
B、被开方数含能开得尽方的因数或因式,故B错误;
C、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故C正确;
D、被开方数含分母,故D错误;
故选:C.
本题考查最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、 (-2,-1)
【解析】
根据关于x轴对称的点的横坐标相等,纵坐标互为相反数,可得答案.
【详解】
点P(﹣2,1),则点P关于x轴对称的点的坐标是(﹣2,﹣1),
故答案是:(﹣2,﹣1).
考查了关于x轴对称的对称点,利用关于x轴对称的点的横坐标相等,纵坐标互为相反数是解题关键.
10、-1.
【解析】
根据分式无意义,分母等于0得,1+x=0,
解得x=﹣1,
故答案为﹣1.
11、且
【解析】
分式的分母不等于零时分式有意义,且还需满足被开方数大于等于零的条件,根据要求列式计算即可.
【详解】
∵代数式有意义,
∴,且,
∴且,
故答案为:且.
此题考查分式有意义的条件,二次根式被开方数的取值范围的确定,正确理解题意列出不等式是解题的关键.
12、
【解析】
试题解析:∵=3﹣x,
∴x-3≤0,
解得:x≤3,
13、(3,3)
【解析】
因为(-2,-1)、(-2,3)两点横坐标相等,长方形有一边平行于y轴,(-2,-1)、(3,-1)两点纵坐标相等,长方形有一边平行于x轴,即可求出第四个顶点的坐标.
【详解】
解:过(﹣2,3)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(3,3),即为第四个顶点坐标.
故答案为:(3,3).
此题考查坐标与图形性质,解题关键在于画出图形
三、解答题(本大题共5个小题,共48分)
14、(1)2;(2)小明摸得两个球得2分的概率为.
【解析】
(1)首先设乙袋中红球的个数为x个,根据题意可得方程:,解此方程即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明摸得两个球得2分的情况,再利用概率公式求解即可求得答案.
【详解】
(1)甲袋中摸出红球的概率为,则乙袋中摸出红球的概率为,
设乙袋中红球的个数为x个,
根据题意得:,
解得:x=2,
经检验,x=2是原分式方程的解,
∴乙袋中红球的个数是2个,
故答案为:2;
(2)画树状图得:
∵共有16种等可能的结果,
又∵摸到白球记1分,摸到黄球记2分,摸到红球记0分,
∴小明摸得两个球得2分的有5种情况,
∴小明摸得两个球得2分的概率为:.
本题考查了分式方程的应用,列表法或树状图法求概率,熟练掌握相关知识是解题的关键. 用到的知识点为:概率=所求情况数与总情况数之比.
15、(1)见解析;(2)⊙O 的直径EC= 1.
【解析】
(1)若要证明AB是⊙O的切线,则可连接AO,再证明AO⊥AB即可.
(2)连接OP,设OG为x,在直角三角形FCG中,由CF和角ACB为10°,利用10°角所对的直角边等于斜边的一半及勾股定理求出CG的长,即可表示出半径OC和OP的长,在直角三角形CGP中利用勾股定理表示出PG的长,然后在直角三角形OPG中,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,然后求出直径即可.
【详解】
证明:(1)连接AO,
∵AB=AC,∠BAC=120°,
∴∠B=∠ACB=10°,
∵AO=CO,
∴∠0AC=∠OCA=10°,
∴∠BAO=120°-10°=90°,
∵OA 是半径
∴AB 是⊙O 的切线;
(2)解:连接OP,
∵PF⊥BC,∴∠FGC=∠EGP=90°,
∵CF=2,∠FCG=10°,∴FG=1,
∴在Rt△FGC 中CG=
∵CP=1.∴Rt△GPC 中,PG=
设OG=x,则OC=x+,连接OP,,显然OP=OC=x+
在 Rt△OPG 中,由勾股定理知
即(x+)2=x2+()2∴x .
∴⊙O 的直径EC=EG+CG=2x++=1.
故答案为:(1)见解析;(2)⊙O 的直径EC= 1.
本题考查圆的切线的判定,常用的切线的判定方法是连接圆心和某一点再证垂直.
16、(1);(2);(3).
【解析】
(1)根据点、的坐标利用待定系数法即可求出直线的表达式;
(2)根据平移的规律“上加下减,左加右减”即可得出平移后的直线表达式;
(3)设直线与轴交点为点,与轴的交点为点,根据一次函数图象上点的坐标特征可求出点、的坐标,再根据直线在第三象限内扫过的图形面积结合三角形的面积公式即可得出结论.
【详解】
解:(1)设直线的表达式为,
将,代入,
得,解得:,
∴直线的表达式为.
(2)根据平移的规律可知:直线:向下平移2个单位后得到的直线表达式为:.
(3)设直线与轴交点为点,与轴的交点为点,
在中,当时,,
∴点的坐标为;
当时,,
∴点的坐标为.
∴直线在第三象限内扫过的图形面积,
,
.
本题考查了一次函数图象与几何变换、待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)根据点的坐标利用待定系数法求出函数表达式;(2)牢记平移的规律“上加下减,左加右减”;(3)结合图形找出直线在第三象限内扫过的图形面积,.
17、左
【解析】
找到横纵坐标的变化情况,根据坐标的平移变换进行分析即可.
【详解】
解:纵坐标没有变化,
横坐标的变化为:,说明向左平移了2个单位长度.
故答案为:左.
本题考查了坐标与图形变化-平移,用到的知识点为:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
18、(1),,;(2),;(3)团有40人,团有10人
【解析】
(1)根据函数图象,用购票款数除以定价的款数,计算即可求出a的值;用第11人到20人的购票款数除以定价的款数,计算即可求出b的值,由图可求m的值;
(2)利用待定系数法求正比例函数解析式求出y1,分x≤10与x>10,利用待定系数法求一次函数解析式求出y2与x的函数关系式即可;
(3)设A团有n人,表示出B团的人数为(50-n),然后分0≤n≤10与n>10两种情况,根据(2)的函数关系式列出方程求解即可.
【详解】
解:(1)在非节假日,人数为10人时,总票价为300,所以人均票价为300÷10=30,因为30÷50=0.6,所以打了6折,a=6.
在节假日,如图x=10时,票价开始发生变化,所以m=10,人数从10人增加到20人,总票价增加了400元,所以此时人均票价为400÷10=40,因为40÷50=0.8,所以打了八折,b=8.
故,,,
(2)在非节假日,设,将(10,300)代入,可得,解得k1=30,故.
在节假日,当时,,当时,设将(10,500),(20,900)代入,可得,解得,故
所以.
(3)设团有n人,团有人,
则当时,根据题意
解得:,∴不合要求.
当时,根据题意
解得:,∴
∴团有40人,团有10人.
本题考查一次函数的应用,(1)结合图象,理解图象上的点代表的意义是解决本题的关键;(2)y1为正比例函数,在图象上找一点代入一般式即可,y2为分段函数,第一段为正比例函数,第二段为一次函数,找到相应的点代入一般式即可求出解析式;(3)设A团有n人,利用方程思想,列出表达式求解即可.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(8,3)
【解析】
根据30度直角三角形的性质得到AD,由勾股定理得到DO,再根据平行线的性质即可得到答案.
【详解】
∵点A坐标为(﹣3,0)
∴AO=3
∵∠ADO=30°,AO⊥DO
∴AD=2AO=6,
∵DO=
∴DO=3
∴D(0,3)
∵四边形ABCD是平行四边形
∴AB=CD=8,AB∥CD
∴点C坐标(8,3)
故答案为(8,3)
本题考查30度直角三角形的性质、勾股定理和平行线的性质,解题的关键是掌握30度直角三角形的性质、勾股定理和平行线的性质.
20、12+4.
【解析】
连接EB、EE′,作EM⊥AB于M,EE′交AD于N.易知△AEB≌△AED≌△ADE′,先求出正方形AMEN的边长,再求出AB,根据S四边形ABFE′=S四边形AEFE′+S△AEB+S△EFB即可解决问题.
【详解】
连接EB、EE′,作EM⊥AB于M,EE′交AD于N,如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,AC⊥BD,AO=OB=OD=OC,
∠DAC=∠CAB=∠DAE′=45°,
在△ADE和△ABE中,
,
∴△ADE≌△ABE(SAS),
∵把△ADE沿AD翻折,得到△ADE′,
∴△ADE≌△ADE′≌△ABE,
∴DE=DE′,AE=AE′,
∴AD垂直平分EE′,
∴EN=NE′,
∵∠NAE=∠NEA=∠MAE=∠MEA=45°,AE=2,
∴AM=EM=EN=AN=2,
∵ED平分∠ADO,EN⊥DA,EO⊥DB,
∴EN=EO=2,AO=2+2,
∴AB=AO=4+2,
∴S△AEB=S△AED=S△ADE′=×2×(4+2)=4+2,S△BDE=S△ADB﹣2S△AEB=×(4+2)2﹣2××2×(4+2)=4,
∵DF=EF,
∴S△EFB=S△BDE=×4=2,
∴S△DEE′=2S△AED﹣S△AEE′=2×(4+2)﹣×(2)2=4+4,S△DFE′=S△DEE′=×(4+4)=2+2,
∴S四边形AEFE′=2S△AED﹣S△DFE′=2×(4+2)﹣(2+2)=6+2,
∴S四边形ABFE′=S四边形AEFE′+S△AEB+S△EFB=6+2+4+2+2=12+4;
故答案为:12+4.
本题考查正方形的性质、翻折变换、全等三角形的性质,角平分线的性质、等腰直角三角形的性质等知识,解题的关键是添加辅助线,学会利用分割法求四边形面积,属于中考填空题中的压轴题.
21、.
【解析】
不等式待定系数的取值范围就是已知不等式或不等式组的解集或特殊解,确定不等式中未知数的系数的取值范围.
【详解】
由得
因为解集为
所以
故答案为:
考核知识点:不等式组解集.会解不等式组是关键.
22、15.
【解析】
中位数有2种情况,共有2n+1个数据时,从小到大排列后,,中位数应为第n+1个数据,可见,大于中位数与小于中位数的数据都为n个;共有2n+2个数据时,从小到大排列后,中位数为中间两个数据平均值,大小介于这两个数据之间,可见大于中位数与小于中位数的数据都为n+1个,所以这组数据中大于或小于这个中位数的数据各占一半,中位数有一个.
【详解】
解:总数据有5个,中位数是从小到大排,第3个数据为中位数,即15为这组数据的中位数.
故答案为:15
本题考查中位数的定义,解题关键是熟练掌握中位数的计算方法,即中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数).
23、-1
【解析】
直接利用零指数幂和负整数指数幂的运算法则进行计算即可.
【详解】
原式=1-3=-1.
故答案为:-1.
本题主要考查实数的运算,掌握零指数幂和负整数指数幂的运算法则是解题的关键.
二、解答题(本大题共3个小题,共30分)
24、(1),;(2);(3)点的坐标为, ,,见解析.
【解析】
(1)利用两点是一次函数上的点求出两点,再代入二次函数求解即可.
(2)根据,求出,求出△ABC.
(3)根据面积为的面积的倍,求出,得出求出此时M的坐标即可.
【详解】
(1)解:∵直线
∴令,则,解得
∴
令,则,∴
将点,代入中得,
,解得
∴抛物线的解析式为:;
令,则,解得
∴.
(2)解:∵,∴
∴
(3)∵面积为的面积的倍,
∴
∵AB=4 ,
∴,
∵
∴抛物线的顶点坐标为符合条件,
当时,,解的,x1=,x2=,
∴点的坐标为(3,-4), ,.
本题考查的是二次函数,熟练掌握二次函数是解题的关键.
25、(1)x1=,x2=1;(2)x1=4+,x2=4﹣
【解析】
(1)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
【详解】
解:(1)2x2﹣3x+1=1,
(2x﹣1)(x﹣1)=1,
2x﹣1=1,x﹣1=1,
x1=,x2=1;
(2)x2﹣8x+1=1,
x2﹣8x=﹣1,
x2﹣8x+16=﹣1+16,
(x﹣4)2=15,
x﹣4=±,
x1=4+,x2=4﹣.
本题考查了解一元二次方程,能选择适当的方法解一元二次方程是解此题的关键.
26、(1)详见解析;(2)当t=10时,▱AEFD是菱形;(3)当t=时,△DEF是直角三角形(∠EDF=90°);当t=1时,△DEF是直角三角形(∠DEF=90°).
【解析】
(1)在Rt△ABC中,根据已知条件求得∠C=30°,由题意可知CD=4tcm,AE=2tcm;在直角△CDF中,根据30°角直角三角形的性质可得DF=CD=2tcm,由此即可证得DF=AE;(2)由DF∥AB,DF=AE,根据一组对边平行且相等的四边形是平行四边形可得四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即可得60﹣4t=2t,解得t=10,即当t=10时,▱AEFD是菱形;(2)能,分∠EDF=90°和∠DEF=90°两种情况求t的值即可.
【详解】
(1)证明:∵在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,
∴∠C=90°﹣∠A=30°.
由题意可知,CD=4tcm,AE=2tcm,
又∵在直角△CDF中,∠C=30°,
∴DF=CD=2tcm,
∴DF=AE;
(2)∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,
解得:t=10,
即当t=10时,▱AEFD是菱形;
(3)当t=时△DEF是直角三角形(∠EDF=90°);当t=1时,△DEF是直角三角形(∠DEF=90°).
理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4tcm,
∴DF=AE=2tcm,
∴AD=2AE=4tcm,
∴4t+4t=60,
∴t=时,∠EDF=90°.
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°,
∵∠A=60°,
∴∠DEA=30°,
∴AD=AE,
AD=AC﹣CD=60﹣4t(cm),AE=DF=CD=2tcm,
∴60﹣4t=t,
解得t=1.
综上所述,当t=时△DEF是直角三角形(∠EDF=90°);当t=1时,△DEF是直角三角形(∠DEF=90°).
本题考查了直角三角形的性质,菱形的判定与性质,正确利用t表示DF、AD的长是解决问题的关键.
题号
一
二
三
四
五
总分
得分
批阅人
年龄/岁
13
14
15
16
人数
1
1
2
1
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)已知,,,是一次函数(为常数)的图像的三点,则,,的大小关系为( )
A.B.C.D.
2、(4分)已知矩形ABCD如图,AB=3,BC=4,AE平分∠BAD交BC于点E,点F、G分别为AD、AE的中点,则FG=( )
A.B.C.2D.
3、(4分)要从甲、乙、丙三名学生中选出一名学生参加数学竞赛,对这三名学生进行了10次数学测试,经过数据分析,3人的平均成绩均为92分,甲的方差为0.024、乙的方差为0.08、丙的方差为0.015,则这10次测试成绩比较稳定的是( )
A.甲B.乙C.丙D.无法确定
4、(4分)下列图案中,既是轴对称图形,又是中心对称图形的是( )
A.B.C.D.
5、(4分)如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=60°,若矩形的对角线长为4,则AD的长是( )
A.2B.4C.2D.4
6、(4分)下列图象中,不能表示是的函数的是( )
A.B.C.D.
7、(4分)如图,小明在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于的长为半径画弧,两弧相交于C、D两点,直线CD即为所求.根据他的作图方法可知四边形一定是( )
A.矩形B.菱形C.正方形D.无法确定
8、(4分)下列式子中属于最简二次根式的是( )
A.B.C.D.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)已知点P(-2,1),则点P关于x轴对称的点的坐标是__.
10、(4分)在分式中,当x=___时分式没有意义.
11、(4分)要使代数式有意义,则的取值范围是________.
12、(4分)若=3-x,则x的取值范围是__________.
13、(4分)一个矩形在直角坐标平面上的三个顶点的坐标分别是(﹣2,﹣1)、(3,﹣1)、(﹣2,3),那么第四个顶点的坐标是_____.
三、解答题(本大题共5个小题,共48分)
14、(12分)在甲、乙两个不透明的口袋中装有质地、大小相同的小球,甲袋中有2个白球,1个黄球和1个红球:乙袋中装有1个白球,1个黄球和若干个红球,从乙盒中仼意摸取一球为红球的概率是从甲盒中仼意摸取一球为红球的概率的2倍.
(1)乙袋中红球的个数为 .
(2)若摸到白球记1分,摸到黄球记2分,摸到红球记0分,小明从甲、乙两袋中先后分别任意摸取一球,请用树状图或列表的方法求小明摸得两个球得2分的概率.
15、(8分)如图,在△ABC 中,AB=AC,∠BAC=120°,E 为 BC 上一点,以 CE 为直径作⊙O 恰好经过 A、C 两点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.
(1)求证:AB 是⊙O 的切线;
(2)如果 CF =2,CP =3,求⊙O 的直径 EC.
16、(8分)已知:点,.
(1)求:直线的表达式;
(2)直接写出直线向下平移2个单位后得到的直线表达式;
(3)求:在(2)的平移中直线在第三象限内扫过的图形面积.
17、(10分)点向__________平移2个单位后,所对应的点的坐标是.
18、(10分)为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打折售票,节假日按团队人数分段定价售票,即人以下(含人)的团队按原价售票;超过人的团队,其中人仍按原价售票,超过人部分的游客打折售票.设某旅游团人数为人,非节假日购票款为(元),节假日购票款为(元).与之间的函数图象如图所示.
(1)观察图象可知: ; ; ;
(2)直接写出,与之间的函数关系式;
(3)某旅行社导游王娜于5月1日带团,5月20日(非节假日)带团都到该景区旅游,共付门票款1900元,,两个团队合计50人,求,两个团队各有多少人?
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)如图,在▱ABCD中,∠ADO=30°,AB=8,点A的坐标为(﹣3,0),则点C的坐标为_____.
20、(4分)如图,正方形ABCD中,对角线AC、BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF、BF、E′F.若AE=2.则四边形ABFE′的面积是_____.
21、(4分)若关于x的一元一次不等式组的的解集为,则a的取值范围是___________.
22、(4分)下表是某校女子羽毛球队队员的年龄分布:
则该校女子排球队队员年龄的中位数为__________岁.
23、(4分)计算:π0-()-1=______.
二、解答题(本大题共3个小题,共30分)
24、(8分)如图,在平面直角坐标系中,直线与轴、轴分别交于两点,抛物线经过两点,与轴交于另一点.
(1)求抛物线解析式及点坐标;
(2)连接,求的面积;
(3)若点为抛物线上一动点,连接,当点运动到某一位置时,面积为的面积的倍,求此时点的坐标.
25、(10分)解方程:
(1)2x2﹣3x+1=1.
(2)x2﹣8x+1=1.(用配方法)
26、(12分)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、C
【解析】
先根据一次函数中k=−3判断出函数的增减性,再根据进行解答即可.
【详解】
解:∵一次函数中k=−3<0,
∴y随x的增大而减小,
∵,
∴.
故选:C.
本题考查的是一次函数图象上点的坐标特点及一次函数的性质,熟知一次函数的增减性是解答此题的关键.
2、D
【解析】
由AE平分∠BAD得∠BAE=∠DAE,根据矩形ABCD可得△ABE是等腰直角三角形,所以BE=AB=3,从而可求EC=1,连接DE,由勾股定理得DE的长,再根据三角形中位线定理可求FG的长.
【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠BEA,
∵AE平分∠BAD
∴∠DAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE=3,
∵BC=AD=4,
∴EC=1,
连接DE,如图,
∴DE=,
∵点F、G分别为AD、AE的中点,
∴FG=.
故选D.
本题考查了矩形的性质以及三角形中位线定理,熟记性质与定理是解题关键.
3、C
【解析】
分析:根据方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定解答即可.
详解:因为3人的平均成绩均为92分,甲的方差为0.024、乙的方差为0.08、丙的方差为0.015,
所以这10次测试成绩比较稳定的是丙,
故选C.
点睛:本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
4、B
【解析】
根据轴对称图形与中心对称图形的概念求解.
【详解】
A.是轴对称图形,不是中心对称图形,故此选项错误;
B.是轴对称图形,也是中心对称图形,故此选项正确;
C.是轴对称图形,不是中心对称图形,因为找不到任何这样的一点,旋转180度后它的两部分能够重合,故此选项错误;
D.是轴对称图形,不是中心对称图形,故此选项错误.
故选B.
本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后两部分重合.
5、C
【解析】
根据矩形性质得出AC=2AO,BD=2BO,AC=BD=4,推出AO=OB=2,得出等边三角形AOB,可得AB=2,由勾股定理可求AD的长.
【详解】
∵四边形ABCD是矩形,
∴AC=2AO,BD=2BO,AC=BD=4,
∴AO=OB=2,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴∠ABO=60°,AB=2=OA
∴
故选:C.
本题考查了等边三角形的性质和判定,矩形的性质的应用,注意:矩形的对角线互相平分且相等.
6、D
【解析】
根据函数的定义可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,可得答案.
【详解】
A、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故A不符合题意;
B、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故B不符合题意;
C、满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故C不符合题意;
D、不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,故D符合题意;
故选:D.
考查了函数的定义,利用了函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
7、B
【解析】
根据菱形的判定方法:四边都相等的四边形是菱形判定即可.
【详解】
根据作图方法可得:,
因此四边形ABCD一定是菱形.
故选:B
本题考查了菱形的判定,解题的关键在于根据四边相等的四边形是菱形判断.
8、C
【解析】
检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
【详解】
解:A、被开方数含分母,故A错误;
B、被开方数含能开得尽方的因数或因式,故B错误;
C、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故C正确;
D、被开方数含分母,故D错误;
故选:C.
本题考查最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.
二、填空题(本大题共5个小题,每小题4分,共20分)
9、 (-2,-1)
【解析】
根据关于x轴对称的点的横坐标相等,纵坐标互为相反数,可得答案.
【详解】
点P(﹣2,1),则点P关于x轴对称的点的坐标是(﹣2,﹣1),
故答案是:(﹣2,﹣1).
考查了关于x轴对称的对称点,利用关于x轴对称的点的横坐标相等,纵坐标互为相反数是解题关键.
10、-1.
【解析】
根据分式无意义,分母等于0得,1+x=0,
解得x=﹣1,
故答案为﹣1.
11、且
【解析】
分式的分母不等于零时分式有意义,且还需满足被开方数大于等于零的条件,根据要求列式计算即可.
【详解】
∵代数式有意义,
∴,且,
∴且,
故答案为:且.
此题考查分式有意义的条件,二次根式被开方数的取值范围的确定,正确理解题意列出不等式是解题的关键.
12、
【解析】
试题解析:∵=3﹣x,
∴x-3≤0,
解得:x≤3,
13、(3,3)
【解析】
因为(-2,-1)、(-2,3)两点横坐标相等,长方形有一边平行于y轴,(-2,-1)、(3,-1)两点纵坐标相等,长方形有一边平行于x轴,即可求出第四个顶点的坐标.
【详解】
解:过(﹣2,3)、(3,﹣1)两点分别作x轴、y轴的平行线,
交点为(3,3),即为第四个顶点坐标.
故答案为:(3,3).
此题考查坐标与图形性质,解题关键在于画出图形
三、解答题(本大题共5个小题,共48分)
14、(1)2;(2)小明摸得两个球得2分的概率为.
【解析】
(1)首先设乙袋中红球的个数为x个,根据题意可得方程:,解此方程即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明摸得两个球得2分的情况,再利用概率公式求解即可求得答案.
【详解】
(1)甲袋中摸出红球的概率为,则乙袋中摸出红球的概率为,
设乙袋中红球的个数为x个,
根据题意得:,
解得:x=2,
经检验,x=2是原分式方程的解,
∴乙袋中红球的个数是2个,
故答案为:2;
(2)画树状图得:
∵共有16种等可能的结果,
又∵摸到白球记1分,摸到黄球记2分,摸到红球记0分,
∴小明摸得两个球得2分的有5种情况,
∴小明摸得两个球得2分的概率为:.
本题考查了分式方程的应用,列表法或树状图法求概率,熟练掌握相关知识是解题的关键. 用到的知识点为:概率=所求情况数与总情况数之比.
15、(1)见解析;(2)⊙O 的直径EC= 1.
【解析】
(1)若要证明AB是⊙O的切线,则可连接AO,再证明AO⊥AB即可.
(2)连接OP,设OG为x,在直角三角形FCG中,由CF和角ACB为10°,利用10°角所对的直角边等于斜边的一半及勾股定理求出CG的长,即可表示出半径OC和OP的长,在直角三角形CGP中利用勾股定理表示出PG的长,然后在直角三角形OPG中,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,然后求出直径即可.
【详解】
证明:(1)连接AO,
∵AB=AC,∠BAC=120°,
∴∠B=∠ACB=10°,
∵AO=CO,
∴∠0AC=∠OCA=10°,
∴∠BAO=120°-10°=90°,
∵OA 是半径
∴AB 是⊙O 的切线;
(2)解:连接OP,
∵PF⊥BC,∴∠FGC=∠EGP=90°,
∵CF=2,∠FCG=10°,∴FG=1,
∴在Rt△FGC 中CG=
∵CP=1.∴Rt△GPC 中,PG=
设OG=x,则OC=x+,连接OP,,显然OP=OC=x+
在 Rt△OPG 中,由勾股定理知
即(x+)2=x2+()2∴x .
∴⊙O 的直径EC=EG+CG=2x++=1.
故答案为:(1)见解析;(2)⊙O 的直径EC= 1.
本题考查圆的切线的判定,常用的切线的判定方法是连接圆心和某一点再证垂直.
16、(1);(2);(3).
【解析】
(1)根据点、的坐标利用待定系数法即可求出直线的表达式;
(2)根据平移的规律“上加下减,左加右减”即可得出平移后的直线表达式;
(3)设直线与轴交点为点,与轴的交点为点,根据一次函数图象上点的坐标特征可求出点、的坐标,再根据直线在第三象限内扫过的图形面积结合三角形的面积公式即可得出结论.
【详解】
解:(1)设直线的表达式为,
将,代入,
得,解得:,
∴直线的表达式为.
(2)根据平移的规律可知:直线:向下平移2个单位后得到的直线表达式为:.
(3)设直线与轴交点为点,与轴的交点为点,
在中,当时,,
∴点的坐标为;
当时,,
∴点的坐标为.
∴直线在第三象限内扫过的图形面积,
,
.
本题考查了一次函数图象与几何变换、待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)根据点的坐标利用待定系数法求出函数表达式;(2)牢记平移的规律“上加下减,左加右减”;(3)结合图形找出直线在第三象限内扫过的图形面积,.
17、左
【解析】
找到横纵坐标的变化情况,根据坐标的平移变换进行分析即可.
【详解】
解:纵坐标没有变化,
横坐标的变化为:,说明向左平移了2个单位长度.
故答案为:左.
本题考查了坐标与图形变化-平移,用到的知识点为:左右移动改变点的横坐标,左减,右加;上下移动改变点的纵坐标,下减,上加.
18、(1),,;(2),;(3)团有40人,团有10人
【解析】
(1)根据函数图象,用购票款数除以定价的款数,计算即可求出a的值;用第11人到20人的购票款数除以定价的款数,计算即可求出b的值,由图可求m的值;
(2)利用待定系数法求正比例函数解析式求出y1,分x≤10与x>10,利用待定系数法求一次函数解析式求出y2与x的函数关系式即可;
(3)设A团有n人,表示出B团的人数为(50-n),然后分0≤n≤10与n>10两种情况,根据(2)的函数关系式列出方程求解即可.
【详解】
解:(1)在非节假日,人数为10人时,总票价为300,所以人均票价为300÷10=30,因为30÷50=0.6,所以打了6折,a=6.
在节假日,如图x=10时,票价开始发生变化,所以m=10,人数从10人增加到20人,总票价增加了400元,所以此时人均票价为400÷10=40,因为40÷50=0.8,所以打了八折,b=8.
故,,,
(2)在非节假日,设,将(10,300)代入,可得,解得k1=30,故.
在节假日,当时,,当时,设将(10,500),(20,900)代入,可得,解得,故
所以.
(3)设团有n人,团有人,
则当时,根据题意
解得:,∴不合要求.
当时,根据题意
解得:,∴
∴团有40人,团有10人.
本题考查一次函数的应用,(1)结合图象,理解图象上的点代表的意义是解决本题的关键;(2)y1为正比例函数,在图象上找一点代入一般式即可,y2为分段函数,第一段为正比例函数,第二段为一次函数,找到相应的点代入一般式即可求出解析式;(3)设A团有n人,利用方程思想,列出表达式求解即可.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(8,3)
【解析】
根据30度直角三角形的性质得到AD,由勾股定理得到DO,再根据平行线的性质即可得到答案.
【详解】
∵点A坐标为(﹣3,0)
∴AO=3
∵∠ADO=30°,AO⊥DO
∴AD=2AO=6,
∵DO=
∴DO=3
∴D(0,3)
∵四边形ABCD是平行四边形
∴AB=CD=8,AB∥CD
∴点C坐标(8,3)
故答案为(8,3)
本题考查30度直角三角形的性质、勾股定理和平行线的性质,解题的关键是掌握30度直角三角形的性质、勾股定理和平行线的性质.
20、12+4.
【解析】
连接EB、EE′,作EM⊥AB于M,EE′交AD于N.易知△AEB≌△AED≌△ADE′,先求出正方形AMEN的边长,再求出AB,根据S四边形ABFE′=S四边形AEFE′+S△AEB+S△EFB即可解决问题.
【详解】
连接EB、EE′,作EM⊥AB于M,EE′交AD于N,如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,AC⊥BD,AO=OB=OD=OC,
∠DAC=∠CAB=∠DAE′=45°,
在△ADE和△ABE中,
,
∴△ADE≌△ABE(SAS),
∵把△ADE沿AD翻折,得到△ADE′,
∴△ADE≌△ADE′≌△ABE,
∴DE=DE′,AE=AE′,
∴AD垂直平分EE′,
∴EN=NE′,
∵∠NAE=∠NEA=∠MAE=∠MEA=45°,AE=2,
∴AM=EM=EN=AN=2,
∵ED平分∠ADO,EN⊥DA,EO⊥DB,
∴EN=EO=2,AO=2+2,
∴AB=AO=4+2,
∴S△AEB=S△AED=S△ADE′=×2×(4+2)=4+2,S△BDE=S△ADB﹣2S△AEB=×(4+2)2﹣2××2×(4+2)=4,
∵DF=EF,
∴S△EFB=S△BDE=×4=2,
∴S△DEE′=2S△AED﹣S△AEE′=2×(4+2)﹣×(2)2=4+4,S△DFE′=S△DEE′=×(4+4)=2+2,
∴S四边形AEFE′=2S△AED﹣S△DFE′=2×(4+2)﹣(2+2)=6+2,
∴S四边形ABFE′=S四边形AEFE′+S△AEB+S△EFB=6+2+4+2+2=12+4;
故答案为:12+4.
本题考查正方形的性质、翻折变换、全等三角形的性质,角平分线的性质、等腰直角三角形的性质等知识,解题的关键是添加辅助线,学会利用分割法求四边形面积,属于中考填空题中的压轴题.
21、.
【解析】
不等式待定系数的取值范围就是已知不等式或不等式组的解集或特殊解,确定不等式中未知数的系数的取值范围.
【详解】
由得
因为解集为
所以
故答案为:
考核知识点:不等式组解集.会解不等式组是关键.
22、15.
【解析】
中位数有2种情况,共有2n+1个数据时,从小到大排列后,,中位数应为第n+1个数据,可见,大于中位数与小于中位数的数据都为n个;共有2n+2个数据时,从小到大排列后,中位数为中间两个数据平均值,大小介于这两个数据之间,可见大于中位数与小于中位数的数据都为n+1个,所以这组数据中大于或小于这个中位数的数据各占一半,中位数有一个.
【详解】
解:总数据有5个,中位数是从小到大排,第3个数据为中位数,即15为这组数据的中位数.
故答案为:15
本题考查中位数的定义,解题关键是熟练掌握中位数的计算方法,即中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数).
23、-1
【解析】
直接利用零指数幂和负整数指数幂的运算法则进行计算即可.
【详解】
原式=1-3=-1.
故答案为:-1.
本题主要考查实数的运算,掌握零指数幂和负整数指数幂的运算法则是解题的关键.
二、解答题(本大题共3个小题,共30分)
24、(1),;(2);(3)点的坐标为, ,,见解析.
【解析】
(1)利用两点是一次函数上的点求出两点,再代入二次函数求解即可.
(2)根据,求出,求出△ABC.
(3)根据面积为的面积的倍,求出,得出求出此时M的坐标即可.
【详解】
(1)解:∵直线
∴令,则,解得
∴
令,则,∴
将点,代入中得,
,解得
∴抛物线的解析式为:;
令,则,解得
∴.
(2)解:∵,∴
∴
(3)∵面积为的面积的倍,
∴
∵AB=4 ,
∴,
∵
∴抛物线的顶点坐标为符合条件,
当时,,解的,x1=,x2=,
∴点的坐标为(3,-4), ,.
本题考查的是二次函数,熟练掌握二次函数是解题的关键.
25、(1)x1=,x2=1;(2)x1=4+,x2=4﹣
【解析】
(1)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
【详解】
解:(1)2x2﹣3x+1=1,
(2x﹣1)(x﹣1)=1,
2x﹣1=1,x﹣1=1,
x1=,x2=1;
(2)x2﹣8x+1=1,
x2﹣8x=﹣1,
x2﹣8x+16=﹣1+16,
(x﹣4)2=15,
x﹣4=±,
x1=4+,x2=4﹣.
本题考查了解一元二次方程,能选择适当的方法解一元二次方程是解此题的关键.
26、(1)详见解析;(2)当t=10时,▱AEFD是菱形;(3)当t=时,△DEF是直角三角形(∠EDF=90°);当t=1时,△DEF是直角三角形(∠DEF=90°).
【解析】
(1)在Rt△ABC中,根据已知条件求得∠C=30°,由题意可知CD=4tcm,AE=2tcm;在直角△CDF中,根据30°角直角三角形的性质可得DF=CD=2tcm,由此即可证得DF=AE;(2)由DF∥AB,DF=AE,根据一组对边平行且相等的四边形是平行四边形可得四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,即可得60﹣4t=2t,解得t=10,即当t=10时,▱AEFD是菱形;(2)能,分∠EDF=90°和∠DEF=90°两种情况求t的值即可.
【详解】
(1)证明:∵在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,
∴∠C=90°﹣∠A=30°.
由题意可知,CD=4tcm,AE=2tcm,
又∵在直角△CDF中,∠C=30°,
∴DF=CD=2tcm,
∴DF=AE;
(2)∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,
即60﹣4t=2t,
解得:t=10,
即当t=10时,▱AEFD是菱形;
(3)当t=时△DEF是直角三角形(∠EDF=90°);当t=1时,△DEF是直角三角形(∠DEF=90°).
理由如下:
当∠EDF=90°时,DE∥BC.
∴∠ADE=∠C=30°
∴AD=2AE
∵CD=4tcm,
∴DF=AE=2tcm,
∴AD=2AE=4tcm,
∴4t+4t=60,
∴t=时,∠EDF=90°.
当∠DEF=90°时,DE⊥EF,
∵四边形AEFD是平行四边形,
∴AD∥EF,
∴DE⊥AD,
∴△ADE是直角三角形,∠ADE=90°,
∵∠A=60°,
∴∠DEA=30°,
∴AD=AE,
AD=AC﹣CD=60﹣4t(cm),AE=DF=CD=2tcm,
∴60﹣4t=t,
解得t=1.
综上所述,当t=时△DEF是直角三角形(∠EDF=90°);当t=1时,△DEF是直角三角形(∠DEF=90°).
本题考查了直角三角形的性质,菱形的判定与性质,正确利用t表示DF、AD的长是解决问题的关键.
题号
一
二
三
四
五
总分
得分
批阅人
年龄/岁
13
14
15
16
人数
1
1
2
1












