第一次月考B卷（人教版）2023-2024学年九年级数学上学期第一次月考

这是一份第一次月考B卷（人教版）2023-2024学年九年级数学上学期第一次月考，文件包含第一次月考B卷人教版全解全析A4版docx、第一次月考B卷人教版参考答案docx、第一次月考B卷人教版考试版测试范围第一章第二章第三章A4版docx、第一次月考B卷人教版答题卡A4版docx、第一次月考B卷人教版答题卡A4版pdf、第一次月考B卷人教版考试版测试范围第一章第二章第三章A3版docx、第一次月考B卷人教版答题卡A3版docx、第一次月考B卷人教版答题卡A3版pdf等8份试卷配套教学资源，其中试卷共55页， 欢迎下载使用。

（考试时间：120分钟 试卷满分：120分）
注意事项：
1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。
4．测试范围：第一章、第二章、第三章（人教版）。
5．考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷
单项选择题（本题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．用配方法解方程x2+10x+9＝0，配方后可得（ ）
A．（x+5）2＝16B．（x+5）2＝1
C．（x+10）2＝91D．（x+10）2＝109
2．由二次函数y＝2（x﹣3）2+1可知（ ）
A．图象开口向下
B．图象向左平移1个单位得到y＝2（x﹣2）2+1
C．图象的对称轴为直线x＝﹣3
D．当x＜3时，y随x的增大而增大
3．已知函数y＝（k﹣3）x2+2x+1的图象与x轴有交点，则k的取值范围是（ ）
A．k＜4B．k≤4C．k＜4且k≠3D．k≤4且k≠3
4．某超市一月份的营业额为200万元，已知第一季度的总营业额共1000万元．如果平均每月增长率为x，则由题意列方程应为（ ）
A．200（1+x）2＝1000
B．200+200×2x＝1000
C．200（1+x）+200（1+x）2＝1000
D．200+200（1+x）+200（1+x）2＝1000
5．若A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y＝2（x+1）2+c上的三个点，则y1，y2，y3的大小关系是（ ）
A．y1＞y2＞y3B．y1＞y3＞y2C．y3＞y2＞y1D．y3＞y1＞y2
6．已知x1，x2是一元二次方程x2﹣6x+3＝0的两个实数根，则x1x2的值为（ ）
A．6B．﹣6C．﹣3D．3
7．奥密克戎是新冠病毒的变异毒株，传染性强，有一人感染了此病毒，未被有效隔离，经过两轮传染，共有121名感染者，在每轮传染中，设平均一个人传染了x人，则可列方程为（ ）
A．1+x＝121B．（1+x）2＝121C．1+x2＝121D．1+x+x2＝121
8．小明在期末体育测试中掷出的实心球的运动路线呈抛物线形．若实心球运动的抛物线的解析式为，其中y是实心球飞行的高度，x是实心球飞行的水平距离．已知该同学出手点A的坐标为，则实心球飞行的水平距离OB的长度为（ ）
A．7mB．7.5mC．8mD．8.5m
9．若x＝﹣1是关于x的一元二次方程ax2+bx﹣1＝0的一个根，则2020+2a﹣2b的值为（ ）
A．2018B．2020C．2022D．2024
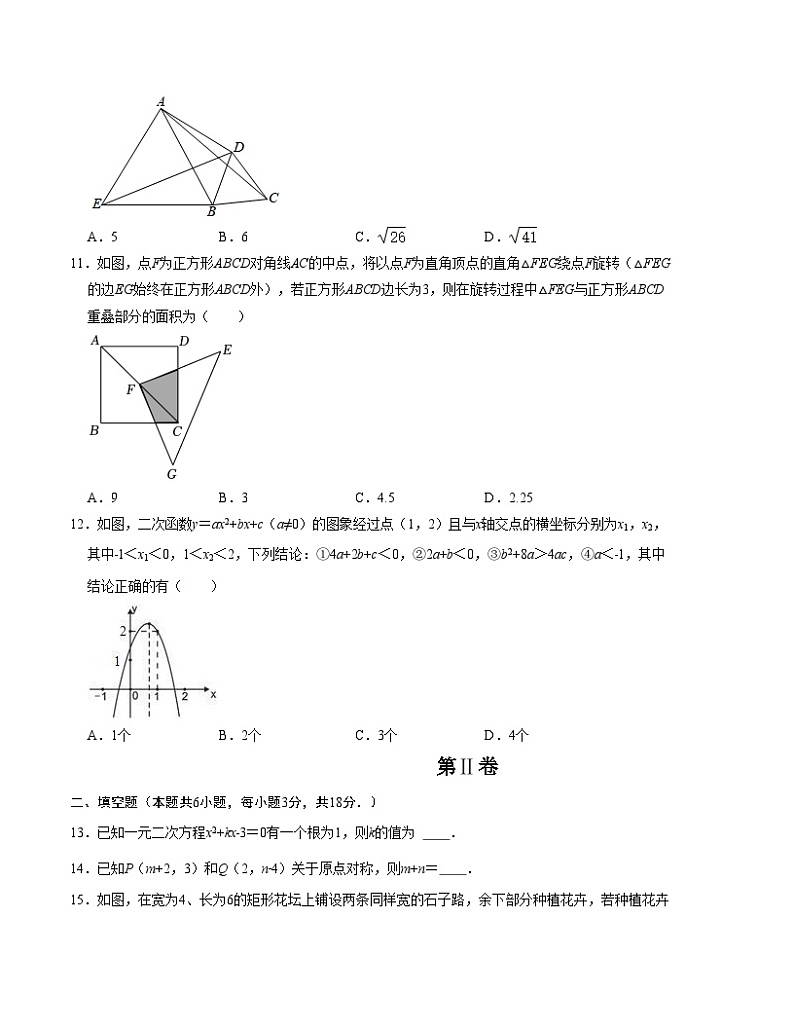
10．如图，四边形ABCD中，∠DAB＝30°，连接AC，将△ABC绕点B逆时针旋转60°，点C的对应点与点D重合，得到△EBD，若AB＝5，AD＝4，则线段AC的长度为（ ）
A．5B．6C．D．
11．如图，点F为正方形ABCD对角线AC的中点，将以点F为直角顶点的直角△FEG绕点F旋转（△FEG的边EG始终在正方形ABCD外），若正方形ABCD边长为3，则在旋转过程中△FEG与正方形ABCD重叠部分的面积为（ ）
A．9B．3C．4.5D．2.25
12．如图，二次函数y＝ax2+bx+c（a≠0）的图象经过点（1，2）且与x轴交点的横坐标分别为x1，x2，其中﹣1＜x1＜0，1＜x2＜2，下列结论：①4a+2b+c＜0，②2a+b＜0，③b2+8a＞4ac，④a＜﹣1，其中结论正确的有（ ）
A．1个B．2个C．3个D．4个
第Ⅱ卷
二、填空题（本题共6小题，每小题3分，共18分．）
13．已知一元二次方程x2+kx﹣3＝0有一个根为1，则k的值为 ．
14．已知P（m+2，3）和Q（2，n﹣4）关于原点对称，则m+n＝ ．
15．如图，在宽为4、长为6的矩形花坛上铺设两条同样宽的石子路，余下部分种植花卉，若种植花卉的面积15，设铺设的石子路的宽为x，依题意可列方程 ．
16．某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线第一象限部分的函数表达式为y＝﹣（x﹣5）2+6，则CD的长为 m．
17．在矩形ABCD中，AB＝3，AD＝5，点E在AD边上，AE＝4，点P为矩形内一点且∠APE＝90°，点M为BC边上一点，连接PA，DM，则PM+DM的最小值为 ．
18．我们定义一种新函数：形如y＝|ax2+bx+c|（a≠0，且b2﹣4a＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y＝|x2﹣2x﹣3|的图象（如图所示），并写出下列五个结论：
①图象与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；
②图象具有对称性，对称轴是直线x＝1；
③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；
④当x＝﹣1或x＝3时，函数的最小值是0；
⑤当x＝1时，函数的最大值是4．
其中正确的结论有 .（填正确的序号）
三、解答题（本题共8小题，共66分．第19-20题每题6分，第21-23题每题8题，其他每题10分，解答应写出文字说明、证明过程或演算步骤．）
19．（6分）解方程：
（1）x2﹣2x﹣15＝0； （2）2x2+3x＝1．
20．（6分）关于x的一元二次方程x2+2x+2m＝0有两个不相等的实数根．
（1）求m的取值范围；
（2）若x1，x2是一元二次方程x2+2x+2m＝0的两个根，且x12+x22＝8，求m的值．
21．（8分）如图，在长为50m、宽为38m的矩形地面内的四周修筑同样宽的道路，余下的铺上草坪．要使草坪的面积为1260m2，道路的宽应为多少？
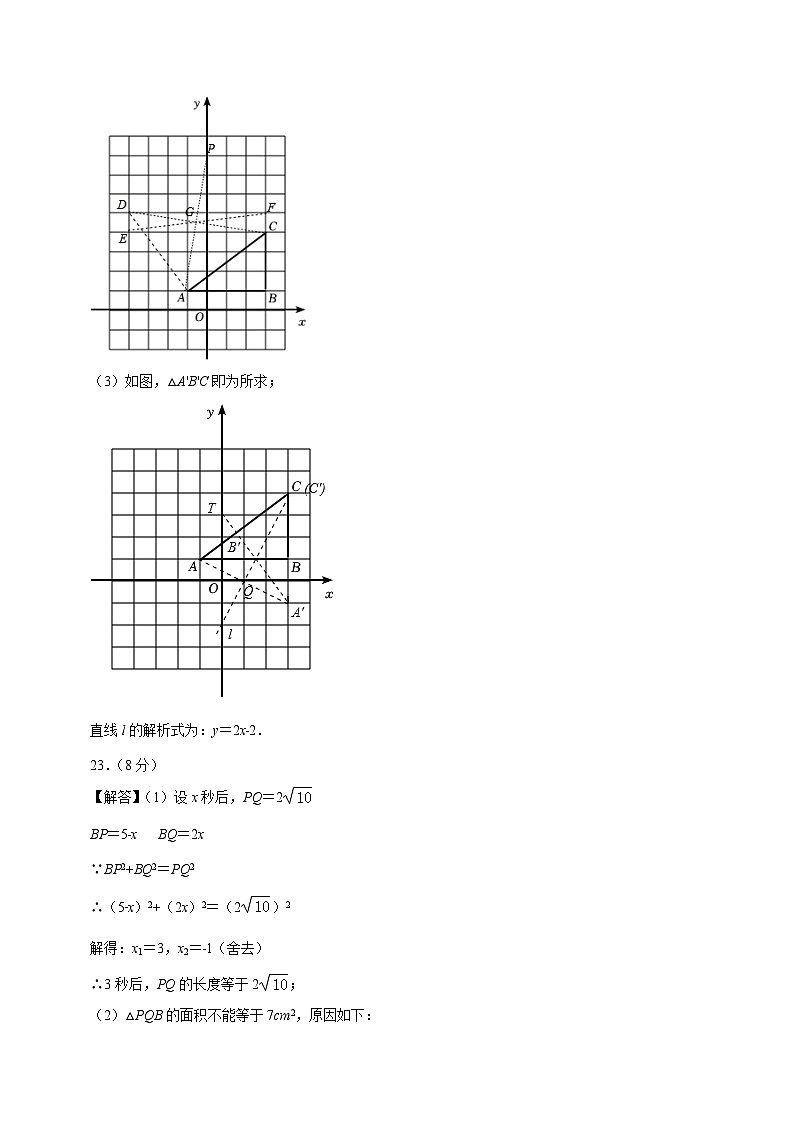
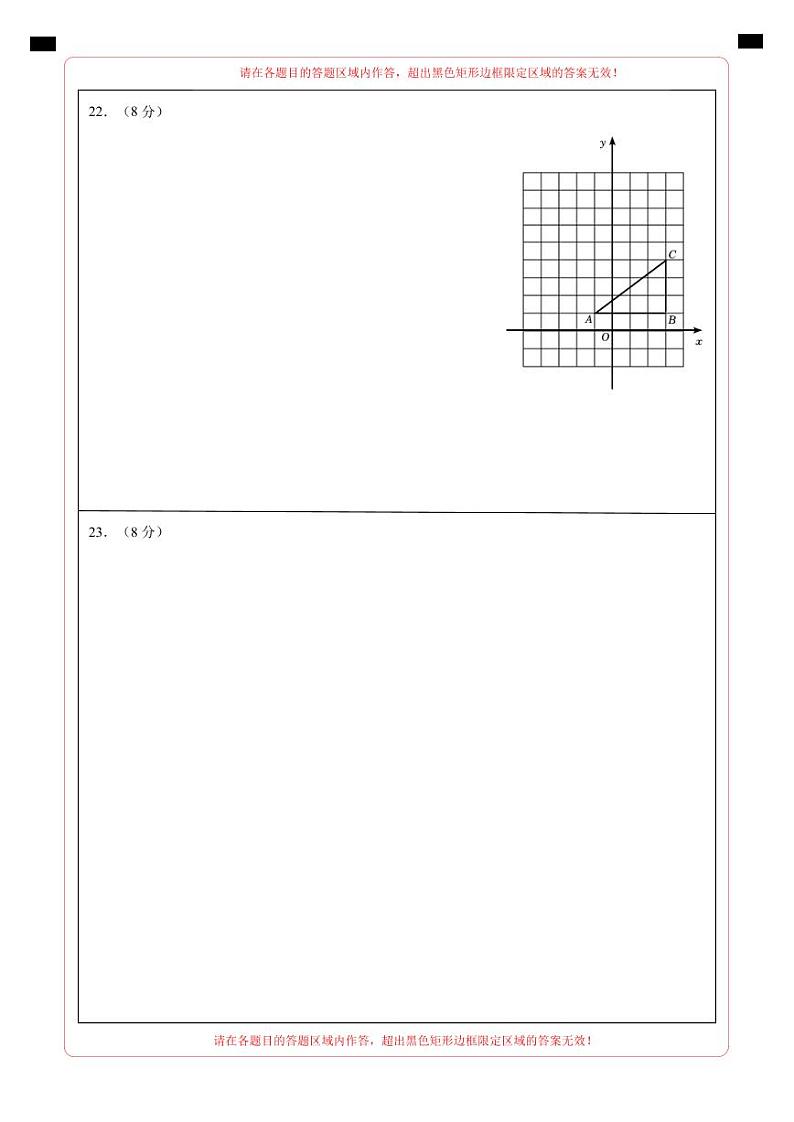
22．（8分）如图，将△ABC放在每个小正方形的边长为1的9×11网格中，点A（﹣1，1）、B（3，1）、C（3，4）均在格点上．
（1）边AC的长等于 ．
（2）请用无刻度的直尺，在所给的网格中画出一个格点P，连接PA，使∠PAC＝45°；
（3）沿过点C直线l，把△ABC翻折，得到△A'B'C，使点B的对应点B'恰好落在边AC上，请在如图所示的网格中，用无刻度的直尺，画出翻折后的图形△A'B'C，并直接写出直线l的解析式．
23．（8分）如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝7cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．
（1）如果P，Q分别从A，B同时出发那么几秒后，PQ的长度等于cm？
（2）在（1）中，△PQB的面积能否等于7cm2？请说明理由．
24．（10分）某超市销售一种国产品牌台灯，平均每天可售出100盏，每盏台灯的利润为12元．为了扩大销售，增加利润，超市准备适当降价，据调查，每盏台灯每降价1元，平均每天会多售出20盏．
（1）若要实现每天销售获利1400元，同时又让消费者得到实惠，则每盏台灯降价多少元？
（2）每盏台灯降价多少元时，商场获利润最大？最大利润是多少元？
25．（10分）问题背景 如图1，在等腰Rt△ABC和等腰Rt△CDE中，AC＝BC，CE＝CD，∠ACB＝∠DCE＝90°，求证：AE＝BD．
尝试应用 如图2，在等腰Rt△ABC中，AC＝BC，∠ACB＝90°，点E是AC边上一点，点F是BE上一点，若∠CFE＝45°，EF＝4，△ABE面积为30，求BF的长．
拓展创新 M是等腰Rt△ABC外一点，∠ACB＝90°，AC＝BC，若∠AMC＝75°，AM＝2，CM＝，直接写出MB的长．
26．（10分）如图，已知抛物线y＝ax2+x+4的对称轴是直线x＝3，且与x轴相交于A、B两点（B点在A点的右侧），与y轴交于C点．
（1）A点的坐标是 ；B点坐标是 ；
（2）直线BC的解析式是： ；
（3）点P是直线BC上方的抛物线上的一动点（不与B、C重合），是否存在点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积，若不存在，试说明理由；
（4）若点M在x轴上，点N在抛物线上，以A、C、M、N为顶点的四边形是平行四边形时，请直接写出点M点坐标．