广东省东莞市长安实验中学2024届九年级下学期中考三模数学试卷(含答案)

这是一份广东省东莞市长安实验中学2024届九年级下学期中考三模数学试卷(含答案)，共19页。

A．±2B．﹣2C．2D．
2．（3分）若|x+3|+（y﹣2）2＝0，那么xy的值为（ ）
A．6B．﹣6C．9D．﹣9
3．（3分）已知单项式3xm+2y与x3yn﹣1是同类项，则m﹣n的值为（ ）
A．1B．﹣1C．3D．﹣3
4．（3分）如图，数轴上表示﹣的点可能是（ ）
A．点EB．点FC．点GD．点H
5．（3分）已知方程x2﹣3x+1＝0的两根是x1，x2，则x1+x2+x1•x2的值是（ ）
A．1B．2C．3D．4
6．（3分）不等式组的解集在数轴上表示正确的是（ ）
A．B．
C．D．
7．（3分）从甲、乙、丙三名男生和A、B两名女生中随机选出一名学生参加问卷调查，则选出女生的可能性是（ ）
A．B．C．D．
8．（3分）如图是某平台销售的折叠椅子及其左视图，已知∠DAB＝60°，CD与地面AB平行，则∠CDE＝（ ）
A．60°B．75°C．110°D．120°
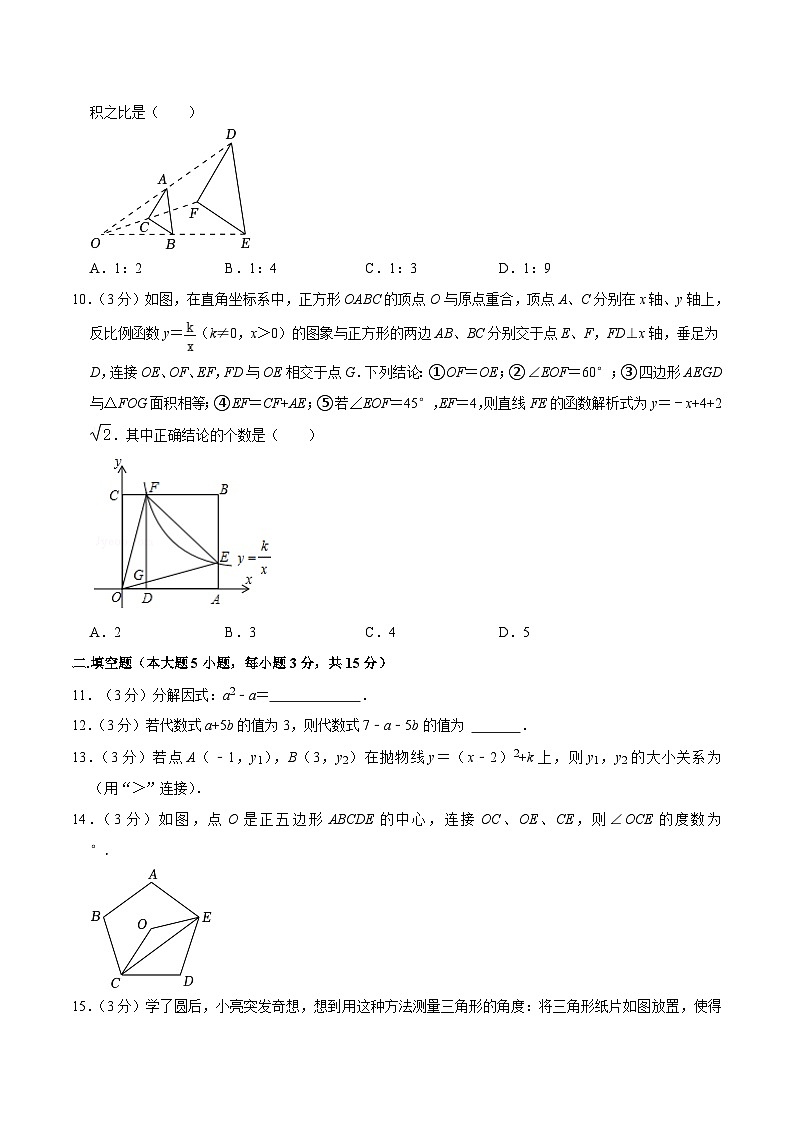
9．（3分）如图，△ABC与△DEF位似，点O是它们的位似中心，其中OA＝AD，则△ABC与△DEF的面积之比是（ ）
A．1：2B．1：4C．1：3D．1：9
10．（3分）如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A、C分别在x轴、y轴上，反比例函数y＝（k≠0，x＞0）的图象与正方形的两边AB、BC分别交于点E、F，FD⊥x轴，垂足为D，连接OE、OF、EF，FD与OE相交于点G．下列结论：①OF＝OE；②∠EOF＝60°；③四边形AEGD与△FOG面积相等；④EF＝CF+AE；⑤若∠EOF＝45°，EF＝4，则直线FE的函数解析式为y＝﹣x+4+2．其中正确结论的个数是（ ）
A．2B．3C．4D．5
二.填空题（本大题5小题，每小题3分，共15分）
11．（3分）分解因式：a2﹣a＝ ．
12．（3分）若代数式a+5b的值为3，则代数式7﹣a﹣5b的值为 ．
13．（3分）若点A（﹣1，y1），B（3，y2）在抛物线y＝（x﹣2）2+k上，则y1，y2的大小关系为 （用“＞”连接）．
14．（3分）如图，点O是正五边形ABCDE的中心，连接OC、OE、CE，则∠OCE的度数为 °．
15．（3分）学了圆后，小亮突发奇想，想到用这种方法测量三角形的角度：将三角形纸片如图放置，使得顶点C在量角器的半圆上，纸片另外两边分别与量角器的半圆交于A，B两点．点A，B在量角器半圆上对应的读数分别是72°，14°，这样小明就能得到∠C的度数，请你帮忙算算∠C的度数是 ．
三.解答题（一）（本大题2小题，每小题5分，共10分）
16．（5分）解方程组：．
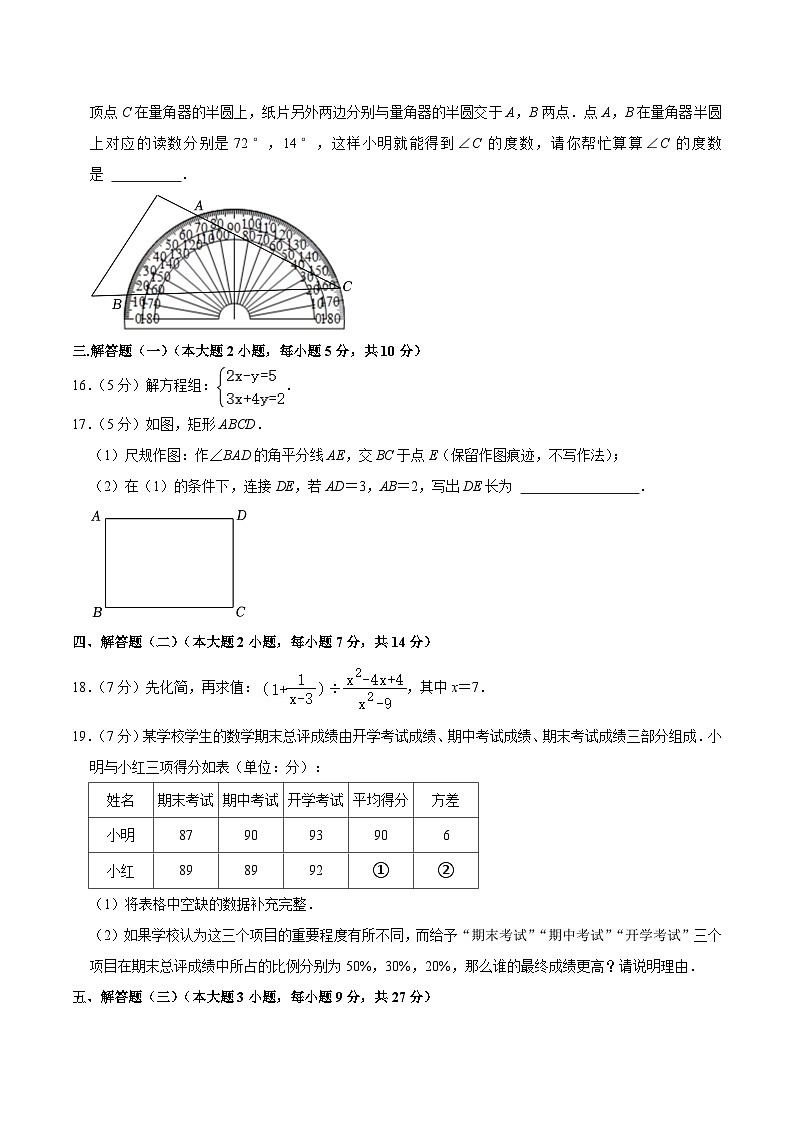
17．（5分）如图，矩形ABCD．
（1）尺规作图：作∠BAD的角平分线AE，交BC于点E（保留作图痕迹，不写作法）；
（2）在（1）的条件下，连接DE，若AD＝3，AB＝2，写出DE长为 ．
四、解答题（二）（本大题2小题，每小题7分，共14分）
18．（7分）先化简，再求值：，其中x＝7．
19．（7分）某学校学生的数学期末总评成绩由开学考试成绩、期中考试成绩、期末考试成绩三部分组成．小明与小红三项得分如表（单位：分）：
（1）将表格中空缺的数据补充完整．
（2）如果学校认为这三个项目的重要程度有所不同，而给予“期末考试”“期中考试”“开学考试”三个项目在期末总评成绩中所占的比例分别为50%，30%，20%，那么谁的最终成绩更高？请说明理由．
五、解答题（三）（本大题3小题，每小题9分，共27分）
20．（9分）如图，有长为30m的篱笆，一面利用墙（墙的最大可用长度为10m），围成中间隔有一道篱笆（平行于AB）的矩形花圃．设花圃的一边AB为x m，面积为y m2．
（1）若要围成面积为63m2的花圃，则AB的长是多少？
（2）求AB为何值时，使花圃面积最大，并求出花圃的最大面积．
21．（9分）【综合与实践】
要测量学校旗杆CD的高度，三个数学研究小组设计了不同的方案，测量方案与数据如表：
（1）根据测量数据，无法计算学校旗杆的高度的小组有第 小组和第 小组；
（2）请选择其中一个可计算的方案及运用其数据求学校旗杆的高度．
22．（9分）如图，在等腰△ABC中，AB＝AC．点D是BC边上的动点，连结AD，将△ADC绕点A旋转至△AEB，使点C与点B重合，连结DE交AB于点F．作EG∥BC交AB于点G，连结CG，交AD于点H．
（1）求证：∠1＝∠2；
（2）求证：△AGH∽△AFD．
六、解答题（四）（本大题2小题，每小题12分，共24分）
23．（12分）如图，AB，CD是⊙O的两条直径，且AB⊥CD，点E是上一动点（不与点B，D重合），连接DE并延长交AB的延长线于点F，点P在AF上，且∠1＝∠2，连接AE，CE分别交OD，OB于点M，N，连接AC，设⊙O的半径为10．
（1）求证：PE是⊙O的切线；
（2）当∠DCE＝15°时，求证：AM＝2ME；
（3）在点E的移动过程中，判断CN•CE是否为定值，若是，求出该定值；若不是，请说明理由．
24．（12分）如图，抛物线y＝ax2+bx+3与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C．
（1）求抛物线的解析式；
（2）如图1，点P是直线AC上方抛物线上的动点，过点P作PE∥x轴交直线AC于点E，作PF∥y轴交直线AC于点F，求E，F两点间距离的最大值；
（3）如图2，连接BC，在抛物线上存在点Q，使∠QAC+∠OCB＝45°，请直接写出符合题意的点Q坐标．
参考答案与试题解析
一.选择题（本大题10小题，每小题3分，共30分）
1．（3分）4的平方根是（ ）
A．±2B．﹣2C．2D．
答案：A．
2．（3分）若|x+3|+（y﹣2）2＝0，那么xy的值为（ ）
A．6B．﹣6C．9D．﹣9
答案：C．
3．（3分）已知单项式3xm+2y与x3yn﹣1是同类项，则m﹣n的值为（ ）
A．1B．﹣1C．3D．﹣3
答案：B．
4．（3分）如图，数轴上表示﹣的点可能是（ ）
A．点EB．点FC．点GD．点H
答案：A．
5．（3分）已知方程x2﹣3x+1＝0的两根是x1，x2，则x1+x2+x1•x2的值是（ ）
A．1B．2C．3D．4
答案：D．
6．（3分）不等式组的解集在数轴上表示正确的是（ ）
A．B．
C．D．
答案：A．
7．（3分）从甲、乙、丙三名男生和A、B两名女生中随机选出一名学生参加问卷调查，则选出女生的可能性是（ ）
A．B．C．D．
答案：B．
8．（3分）如图是某平台销售的折叠椅子及其左视图，已知∠DAB＝60°，CD与地面AB平行，则∠CDE＝（ ）
A．60°B．75°C．110°D．120°
答案：D．
9．（3分）如图，△ABC与△DEF位似，点O是它们的位似中心，其中OA＝AD，则△ABC与△DEF的面积之比是（ ）
A．1：2B．1：4C．1：3D．1：9
答案：B．
10．（3分）如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A、C分别在x轴、y轴上，反比例函数y＝（k≠0，x＞0）的图象与正方形的两边AB、BC分别交于点E、F，FD⊥x轴，垂足为D，连接OE、OF、EF，FD与OE相交于点G．下列结论：①OF＝OE；②∠EOF＝60°；③四边形AEGD与△FOG面积相等；④EF＝CF+AE；⑤若∠EOF＝45°，EF＝4，则直线FE的函数解析式为y＝﹣x+4+2．其中正确结论的个数是（ ）
A．2B．3C．4D．5
答案：B．
二.填空题（本大题5小题，每小题3分，共15分）
11．（3分）分解因式：a2﹣a＝ a（a﹣1） ．
答案：a2﹣a＝a（a﹣1）．
12．（3分）若代数式a+5b的值为3，则代数式7﹣a﹣5b的值为 4 ．
答案：4．
13．（3分）若点A（﹣1，y1），B（3，y2）在抛物线y＝（x﹣2）2+k上，则y1，y2的大小关系为 ＞ （用“＞”连接）．
答案：＞．
14．（3分）如图，点O是正五边形ABCDE的中心，连接OC、OE、CE，则∠OCE的度数为 18 °．
答案：18．
15．（3分）学了圆后，小亮突发奇想，想到用这种方法测量三角形的角度：将三角形纸片如图放置，使得顶点C在量角器的半圆上，纸片另外两边分别与量角器的半圆交于A，B两点．点A，B在量角器半圆上对应的读数分别是72°，14°，这样小明就能得到∠C的度数，请你帮忙算算∠C的度数是 29° ．
答案：29°．
三.解答题（一）（本大题2小题，每小题5分，共10分）
16．（5分）解方程组：．
解：，
①×4+②得：11x＝22，
解得：x＝2，
把x＝2代入①得：4﹣y＝5，
解得：y＝﹣1，
则方程组的解为．
17．（5分）如图，矩形ABCD．
（1）尺规作图：作∠BAD的角平分线AE，交BC于点E（保留作图痕迹，不写作法）；
（2）在（1）的条件下，连接DE，若AD＝3，AB＝2，写出DE长为 ．
解：（1）如图所示；线段AE即为所求；
（2）∵四边形ABCD是矩形，
∴∠BAD＝90°，BC＝AD＝3，CD＝AB＝2，
∵AE平分∠BAD，
∴∠BAE＝∠DAE，
∵AD∥BC，
∴∠DAE＝∠AEB，
∴∠BAE＝∠AEB，
∴AB＝BE＝2，
∴CE＝BC﹣BE＝1，
∴DE＝＝＝，
四、解答题（二）（本大题2小题，每小题7分，共14分）
18．（7分）先化简，再求值：，其中x＝7．
解：
＝
＝，
当x＝7，
原式＝＝2．
19．（7分）某学校学生的数学期末总评成绩由开学考试成绩、期中考试成绩、期末考试成绩三部分组成．小明与小红三项得分如表（单位：分）：
（1）将表格中空缺的数据补充完整．
（2）如果学校认为这三个项目的重要程度有所不同，而给予“期末考试”“期中考试”“开学考试”三个项目在期末总评成绩中所占的比例分别为50%，30%，20%，那么谁的最终成绩更高？请说明理由．
解：（1）由题意得，表格中①的值为：＝90；
②的值为：[（89﹣90）2×2+（92﹣90）2]＝2；
（2）小红的最终成绩更高，理由如下：
小明的最终成绩为：87×50%+90×30%+93×20%＝89.1（分），
小红的最终成绩为：89×50%+89×30%+92×20%＝89.6（分），
因为89.6＞89.1，
所以小红的最终成绩更高．
五、解答题（三）（本大题3小题，每小题9分，共27分）
20．（9分）如图，有长为30m的篱笆，一面利用墙（墙的最大可用长度为10m），围成中间隔有一道篱笆（平行于AB）的矩形花圃．设花圃的一边AB为x m，面积为y m2．
（1）若要围成面积为63m2的花圃，则AB的长是多少？
（2）求AB为何值时，使花圃面积最大，并求出花圃的最大面积．
解：（1）x（30﹣3x）＝63
30x﹣3x2＝63
3x2﹣30x+63＝0
x2﹣10x+21＝0
（x﹣3）（x﹣7）＝0．
解得：x1＝3，x2＝7．
当x＝3时，30﹣3x＝21＞10，不合题意，舍去；
当x＝7时，30﹣3x＝9＜10，符合题意．
答：若要围成面积为63m2的花圃，AB的长为7 m；
（2）y＝x（30﹣3x）
＝﹣3x2+30x
＝﹣3（x2﹣10x+25）+75
＝﹣3（x﹣5）2+75．
∵0＜30﹣3x≤10，
∴≤x＜10．
∴当x＝时，y最大．最大面积为：×（30﹣3×）＝ （m2）．
答：AB为m时，花圃面积最大，花圃的最大面积为m2．
21．（9分）【综合与实践】
要测量学校旗杆CD的高度，三个数学研究小组设计了不同的方案，测量方案与数据如表：
（1）根据测量数据，无法计算学校旗杆的高度的小组有第 一 小组和第 三 小组；
（2）请选择其中一个可计算的方案及运用其数据求学校旗杆的高度．
解：（1）第一，第三小组的数据无法算出大楼高度，
理由：第一小组只测量了AO＝1.5m，AD＝16.5m，没有测量AB长度，所以第一小组的数据无法算出大楼高度，
第三小组只测量了AE＝0.4m，EF＝0.2m，AB＝1.8m．没有测量线段EM或AM的长度，所以第三小组的数据无法算出大楼高度，
答案：一，三；
（2）第二小组的方案：
在Rt△EFD中，∠EFD＝90°，∠DEF＝30°，DF＝AE＝2.2m，
∴EF＝＝≈3.81（m），
在Rt△EFC中，∠EFC＝90°，∠CEF＝60°，
FC＝EF•tan∠CEF＝3.81×≈6.59（m），
∴DC＝DF+FC≈8.8（m），
答：学校旗杆的高度约为8.8m．
22．（9分）如图，在等腰△ABC中，AB＝AC．点D是BC边上的动点，连结AD，将△ADC绕点A旋转至△AEB，使点C与点B重合，连结DE交AB于点F．作EG∥BC交AB于点G，连结CG，交AD于点H．
（1）求证：∠1＝∠2；
（2）求证：△AGH∽△AFD．
证明：（1）∵EG∥BC，
∴∠2＝∠ABC，
∵AB＝AC，
∴∠ACB＝∠ABC，
由旋转的性质得到：∠1＝∠ACB，
∴∠1＝∠2；
（2）∵∠1＝∠2，
∴EG＝EB，
由旋转的性质得到：CD＝BE，
∴EG＝CD，
∵GE∥CD，
∴四边形DCGE是平行四边形，
∴GH∥FD，
∴△AGH∽△AFD．
六、解答题（四）（本大题2小题，每小题12分，共24分）
23．（12分）如图，AB，CD是⊙O的两条直径，且AB⊥CD，点E是上一动点（不与点B，D重合），连接DE并延长交AB的延长线于点F，点P在AF上，且∠1＝∠2，连接AE，CE分别交OD，OB于点M，N，连接AC，设⊙O的半径为10．
（1）求证：PE是⊙O的切线；
（2）当∠DCE＝15°时，求证：AM＝2ME；
（3）在点E的移动过程中，判断CN•CE是否为定值，若是，求出该定值；若不是，请说明理由．
（1）证明：连接OE，如图，
∵CD为⊙O的直径，
∴∠CED＝90°，
∴∠OED+∠OEC＝90°，
∵OC＝OE，
∴∠2＝∠OCE，
∴∠2+∠OED＝90°，
∵∠1＝∠2，
∴∠1+∠OED＝90°，
∴∠OEP＝180°﹣∠OED﹣∠1＝180°﹣90°＝90°，
∴OE⊥PE，
∴OE为⊙O的半径，
∴PE是⊙O的切线；
（2）证明：∵∠DCE＝15°，
∴∠DOE＝2∠2＝30°，
∵AB⊥CD，
∴∠AOD＝90°，
∴∠AOE＝120°，
∵OA＝OE，
∴＝30°，
∴，∠AMO＝90°﹣∠OAE＝60°，
∵∠OMA＝∠DOE+∠OEM，
∴∠OEM＝30°，
∴∠OEM＝∠DOE＝30°，
∴OM＝ME，
∴AM＝2ME．
（3）解：CN•CE是定值，为200，
∵AB⊥CD，
∴∠COB＝90°，
∵∠CED＝90°，
∴∠COB＝∠CED＝90°，
∵∠OCE＝∠OCE，
∴△CON∽△CED，
∴，
∴CN•CE＝CO•CD＝10×（2×10）＝200，
∴CN•CE是定值，为200．
24．（12分）如图，抛物线y＝ax2+bx+3与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C．
（1）求抛物线的解析式；
（2）如图1，点P是直线AC上方抛物线上的动点，过点P作PE∥x轴交直线AC于点E，作PF∥y轴交直线AC于点F，求E，F两点间距离的最大值；
（3）如图2，连接BC，在抛物线上存在点Q，使∠QAC+∠OCB＝45°，请直接写出符合题意的点Q坐标．
解：（1）∵抛物线y＝ax2+bx+3与x轴交于A（﹣3，0），B（1，0）两点，
∴，
解得：，
∴抛物线的解析式为y＝﹣x2﹣2x+3；
（2）由抛物线的表达式知，点C（0，3），
∴OC＝3，
∵A（﹣3，0），
∴OA＝3，
∴OA＝OC，
∴△CAO为等腰直角三角形，则∠ACO＝∠CAO＝45°，
∵PE∥x轴，PF∥y轴，
∴∠PFE＝∠ACO＝45°，∠PEF＝∠CAO＝45°，
∴△PEF是等腰直角三角形，
∴EF＝PF，
由点A、C的坐标得：直线AC的表达式为：y＝x+3，
设点P（x，﹣x2﹣2x+3），则点F（x，x+3），
∴PF＝（﹣x2﹣2x+3）﹣（x+3）＝﹣x2﹣3x，
∵﹣1＜0，
故PF有最大值，当x＝﹣时，PF的最大值为：，
则EF的最大值为：；
（3）当点Q在AC下方时，如图，设AQ交y轴于点H，
∵∠QAC+∠QAB＝45°，∠QAC+∠OCB＝45°，
∴∠OCB＝∠QAB，
∴tan∠OCB＝tan∠QAB，
∴＝，即＝，
∴OH＝1，
则直线AH的表达式为：y＝（x+3），
联立上式和抛物线的表达式得：﹣x2﹣2x+3＝（x+3），
解得：x＝﹣3（舍去）或x＝，
则点Q（，）；
当点Q在AC上方时，如图，过点A作AM⊥x轴，使AM＝OA＝3，连接CM，在线段MC上截取MN＝1，连接AN，
∵∠OAM+∠AOC＝90°+90°＝180°，
∴AM∥OC，
∵AM＝OC，
∴四边形AOCM是平行四边形，
∵∠AOC＝90°，
∴四边形AOCM是矩形，
则∠M＝90°＝∠BOC，
∵MN＝OB＝1，
∴△AMN≌△COB（SAS），
∴∠MAN＝∠OCB，
∵∠CAM＝90°﹣∠CAO＝45°，
∴∠MAN+∠CAN＝45°，
∵∠QAC+∠OCB＝45°，
∴∠CAN＝∠QAC，
∵A（﹣3，0），N（﹣2，3），
∴直线AN的表达式为：y＝3（x+3），
联立上式和抛物线的表达式得：﹣x2﹣2x+3＝3（x+3），
解得：x＝﹣3（舍去）或﹣2，
则点Q（﹣2，3）；
综上，点Q的坐标为（，）或（﹣2，3）．姓名
期末考试
期中考试
开学考试
平均得分
方差
小明
87
90
93
90
6
小红
89
89
92
①
②
课题
测量学校旗杆的高度
测量工具
测量角度的仪器，皮尺，小镜子，直角三角形纸板等
测量小组
第一小组
第二小组
第三小组
测量方案示意图



说明
利用镜子反射测量旗杆的高度，点O为镜子，眼睛B看到镜子中的旗杆顶端C．
先测量观测台EA的高，再在观测点E处测得旗杆顶端C点的仰角∠CEF，旗杆底端D点的俯角∠DEF．（其中EF⊥CD于F）
利用直角三角形纸板的直角边AE保持水平，并且边AE与点M在同一直线上，直角三角板的斜边AF与旗杆顶端C在同一直线上．
测量数据
AO＝1.5m，AD＝16.5m．
EA＝2.2m，∠CEF＝60°，∠DEF＝30°．
AE＝0.4m，EF＝0.2m，AB＝1.8m．
姓名
期末考试
期中考试
开学考试
平均得分
方差
小明
87
90
93
90
6
小红
89
89
92
①
②
课题
测量学校旗杆的高度
测量工具
测量角度的仪器，皮尺，小镜子，直角三角形纸板等
测量小组
第一小组
第二小组
第三小组
测量方案示意图



说明
利用镜子反射测量旗杆的高度，点O为镜子，眼睛B看到镜子中的旗杆顶端C．
先测量观测台EA的高，再在观测点E处测得旗杆顶端C点的仰角∠CEF，旗杆底端D点的俯角∠DEF．（其中EF⊥CD于F）
利用直角三角形纸板的直角边AE保持水平，并且边AE与点M在同一直线上，直角三角板的斜边AF与旗杆顶端C在同一直线上．
测量数据
AO＝1.5m，AD＝16.5m．
EA＝2.2m，∠CEF＝60°，∠DEF＝30°．
AE＝0.4m，EF＝0.2m，AB＝1.8m．