泰安市泰山区东岳中学2024-2025学年七年级数学第一次月考数学试题和答案

这是一份泰安市泰山区东岳中学2024-2025学年七年级数学第一次月考数学试题和答案，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1、下列各组数中不可能是一个三角形的边长的是（ ）
A 5，12，13 B 5，7，7 C 1，2，3 D 30，40，50
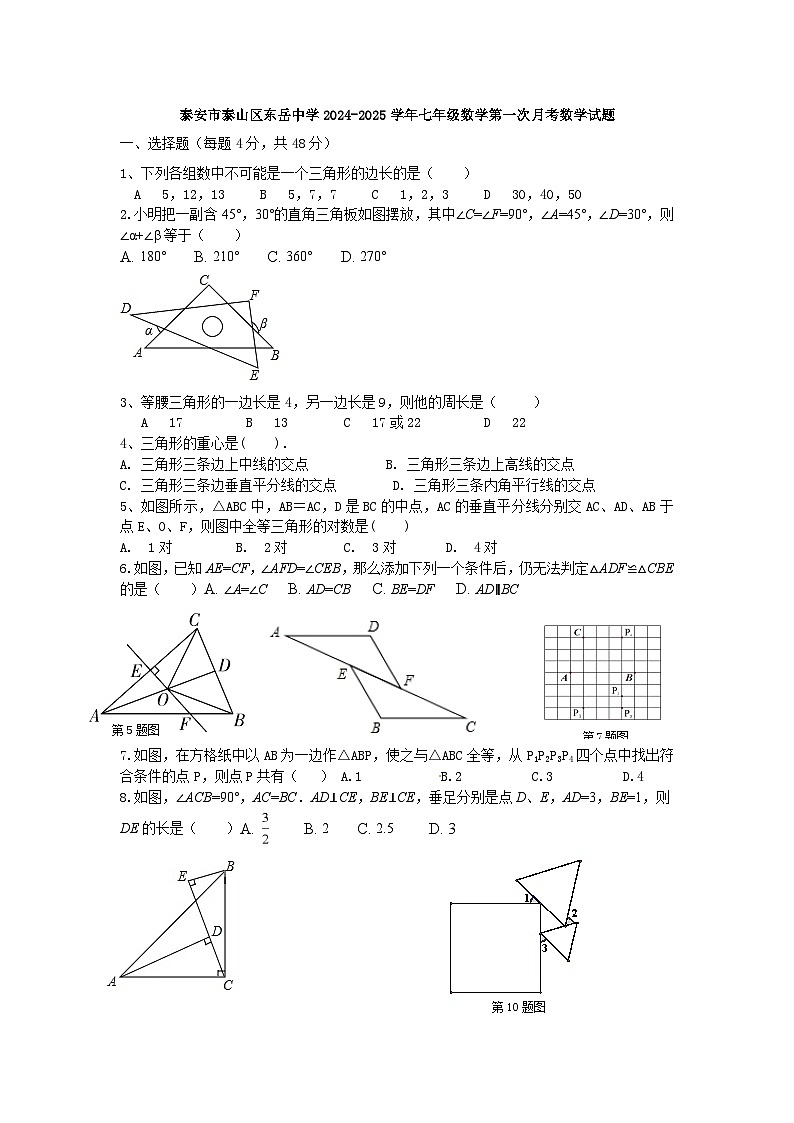
2.小明把一副含45°，30°的直角三角板如图摆放，其中∠C=∠F=90°，∠A=45°，∠D=30°，则∠α+∠β等于（ ）
A. 180° B. 210° C. 360° D. 270°
3、等腰三角形的一边长是4，另一边长是9，则他的周长是（ ）
A 17 B 13 C 17或22 D 22
4、三角形的重心是( )．
A. 三角形三条边上中线的交点 B. 三角形三条边上高线的交点
C. 三角形三条边垂直平分线的交点 D. 三角形三条内角平行线的交点
5、如图所示，△ABC中，AB＝AC，D是BC的中点，AC的垂直平分线分别交AC、AD、AB于点E、O、F，则图中全等三角形的对数是( )
A. 1对 B. 2对 C. 3对 D. 4对
第5题图
6.如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（ ）A. ∠A=∠CB. AD=CBC. BE=DFD. AD∥BC
第7题图
7.如图，在方格纸中以AB为一边作△ABP，使之与△ABC全等，从P1P2P3P4四个点中找出符合条件的点P，则点P共有（ ） A.1 B.2 C.3 D.4
8.如图，∠ACB=90°，AC=BC．AD⊥CE，BE⊥CE，垂足分别是点D、E，AD=3，BE=1，则DE的长是（ ）A. B. 2 C. 2.5 D. 3
第10题图

9.已知一等腰三角形的腰长为5，底边长为4，底角为α．满足下列条件的三角形与已知三角形不一定全等的是（ ）
A. 两个角是α，它们的夹边为4 B. 三条边长分别是4，5，5
C. 两条边长分别为4，5，它们的夹角为α D. 两条边长是5，一个角是α
10、一个正方形和两个等边三角形的位置如图所示，若∠3=50°则∠1+∠2的值为（ ）
A 90° B 100° C 130° D 180°
11.如图1，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示三角形的高的线段共有（ ）
A．2条 B．3条 C．4条 D．5条
12.下列四个图形中，线段BE是△ABC的高的是 （ ）

二、填空题（每题4分，共24分）
13.如左图，在△ABC中，BO、CO分别平分∠ABC、∠ACB．若∠BOC=110°，则∠A=______．
第15题图

14.在△ABC中，AB=5，AC=3，AD是BC边上的中线，则AD的取值范围是______．
15、如图所示，在△ABC中，∠ABC = ∠ACB，∠A = 40°，P是△ABC内一点，且∠1 = ∠2，则∠BPC=________.
16.如右图所示，O为△ABC的三条角平分线的交点，∠BOC=120°，则∠CAB=________度．
17、如图，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，连接AC。若AC=6，则四边形ABCD的面积为
18．如图，一块三角形玻璃板，不小心摔成三块，小亮要想得到一块与原来一样的三角形玻璃板，需要带着哪一块去商店，让师傅割出来，依据是
A．①，SSSB．②，ASAC．③ ，AAS D．
第17题图
三、解答题：（7个小题，共计78分）
19．（10分）如图，△ABC中，∠BAC=90°，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直线于E，直线CE交BA的延长线于F．试说明：BD=2CE．

20．（10分）两个大小不同的等腰直角三角形的三角板如图1所示位置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC。
（1）请找出图2中的全等三角形，并给予证明（注：结论中不能含有未标识的字母）
（2）问：DC⊥BE吗？请说明理由。

21.（1）如图，为中线，点E在上，交于点F，，求证：．

（2）如图，是的中线，E是上一点，交于F，若，，，求线段的长度．

22.已知：在中，，D、E分别为上的点，且交于点F．若为的角平分线．(1)求的度数；(2)若，求的长．

23.如图，已知：在中，，、是的角平分线，交于点O求证：．

24.图1、图2中，点B为线段AE上一点，△ABC与△BED都是等边三角形。(1)如图1，求证：AD=CE；(2)如图2，设CE与AD交于点F，连接BF.①求证：∠CFA=600；②求证：CF+BF=AF.

25.现有正方形ABCD和一个以O为直角顶点的三角板，移动三角板，使三角板两直角边所在直线分别与直线BC、CD交于点M、N．
(1)如图1，若点O与点A重合，则OM与ON的数量关系是________
(2)如图2，若点O在正方形的中心（即两对角线交点），则（1）中的结论是否仍然成立？请说明理由；
(3)如图3，若点O在正方形的内部（含边界），当OM=ON时，请探究点O在移动过程中可形成什么图形？
(4)如图4，是点O在正方形外部的一种情况．当OM=ON时，请你就“点O的位置在各种情况下（含外部）移动所形成的图形”提出一个正确的结论．（不必说明）
泰安市泰山区东岳中学2024-2025学年七年级数学第一次月考数学试题答案
一、选择题
1.C 2.B 3. D 4.A 5. D 6. B 7. C 8.B 9. D 10. B 11.D 12.D
二、填空题
13.40 14. 1＜AD＜4 15.110° 16.600 16. 18 18.③，ASA
三、解答题：
19. 先通过ASA证明△ABD≌△ACF，得出BD＝CF,再通过ASA证明△FBE≌△CBE，得出CE＝EF,从而得出结论
20. （1）△ABE≌△ACD，证明略，提示：用SAS证明
（2）DC⊥BE，理由是∵△ABE≌△ACD，∴∠ACD=∠B=45°，又∵∠ACB=45°，∴∠BCD=∠ACD+∠ACB=45°+45°=90°∴DC⊥BE
21.解：如图，延长至点，使，连接．
为的中线，
．
在和中，
，
，
，．
，
．
，
，
，
．
（2）.解：如图，延长到G，使，连接，

∵是的中线
∴，
在和中，
，
∴，
∴，
∵，
∴，
∴，
∴，
∴，
∴，
∴
22.（1）解：∵为的角平分线，
∴
∵，
∴，
∴
（2）解：在上截取，连接．
∵为的角平分线．
∴，
∵，
∴，
∵
∴，
∴
∴，
又∵，
∴
∴，
∴
23.证明：如图，在上取一点H，使，连接．
∵是的角平分线，
∴，
在和中，
∵
∴，
∴，
∵是的角平分线，
∴，
∵，
∴，
∵、是的角平分线，
∴，
∴，
在和中，
∴，
∴，
∵，
∴．
24.证明：（1）如图1，∵△ABC与△BED都是等边三角形，
∴BD=BE，AB=BC，∠ABC=∠DBE=60°，
∴∠ABC+∠CBD=∠DBE+∠CBD，
即∠ABD=∠CBE，
在△ABD和△CBE中，
∵AB=AC，∠ABD=∠CBE，BD=BE
∴△ABD≌△CBE（SAS），
∴AD=CE，
（2）①如图2，由（1）得：△ABD≌△CBE，
∴∠BCE=∠DAB，
∵∠ABC=∠BCE+∠CEB=60°，
∴∠ABC=∠DAB+∠CEB=60°，
∵∠CFA=∠DAB+∠CEB，
∴∠CFA=60°，
②如图3，在AF上取一点G，使FG=CF，连接CG，
∵∠AFC=60°，
∴△CGF是等边三角形，
∴∠GCF=60°，CG=CF，
∴∠GCB+∠BCE=60°，
∵∠ACB=60°，
∴∠ACG+∠GCB=60°，
∴∠ACG=∠BCE，
∵AC=BC，
∴△ACG≌△BCF，
∴AG=BF，
∵AF=AG+GF，
∴AF=BF+CF．
25.（1）OM=ON
（2）解：仍成立．
证明：如图2，
连接AC、BD，则
由正方形ABCD可得，∠BOC=90°，BO=CO，∠OBM=∠OCN=45°
∵∠MON=90°
∴∠BOM=∠CON
在△BOM和△CON中
∴△BOM≌△CON（ASA）
∴OM=ON.
（3）解：如图3，
过点O作OE⊥BC，作OF⊥CD，垂足分别为E、F，则∠OEM=∠OFN=90°
又∵∠C=90°
∴∠EOF=90°=∠MON
∴∠MOE=∠NOF
在△MOE和△NOF中
∴△MOE≌△NOF（AAS）
∴OE=OF
又∵OE⊥BC，OF⊥CD
∴点O在∠C的平分线上
∴O在移动过程中可形成线段AC．
（4）解：O在移动过程中可形成直线AC．