高三数学一轮复习五层训练(新高考地区)第8练二次函数与幂函数(原卷版+解析)

这是一份高三数学一轮复习五层训练(新高考地区)第8练二次函数与幂函数(原卷版+解析)，共21页。试卷主要包含了课本变式练，考点分类练，最新模拟练，高考真题练，综合提升练等内容，欢迎下载使用。

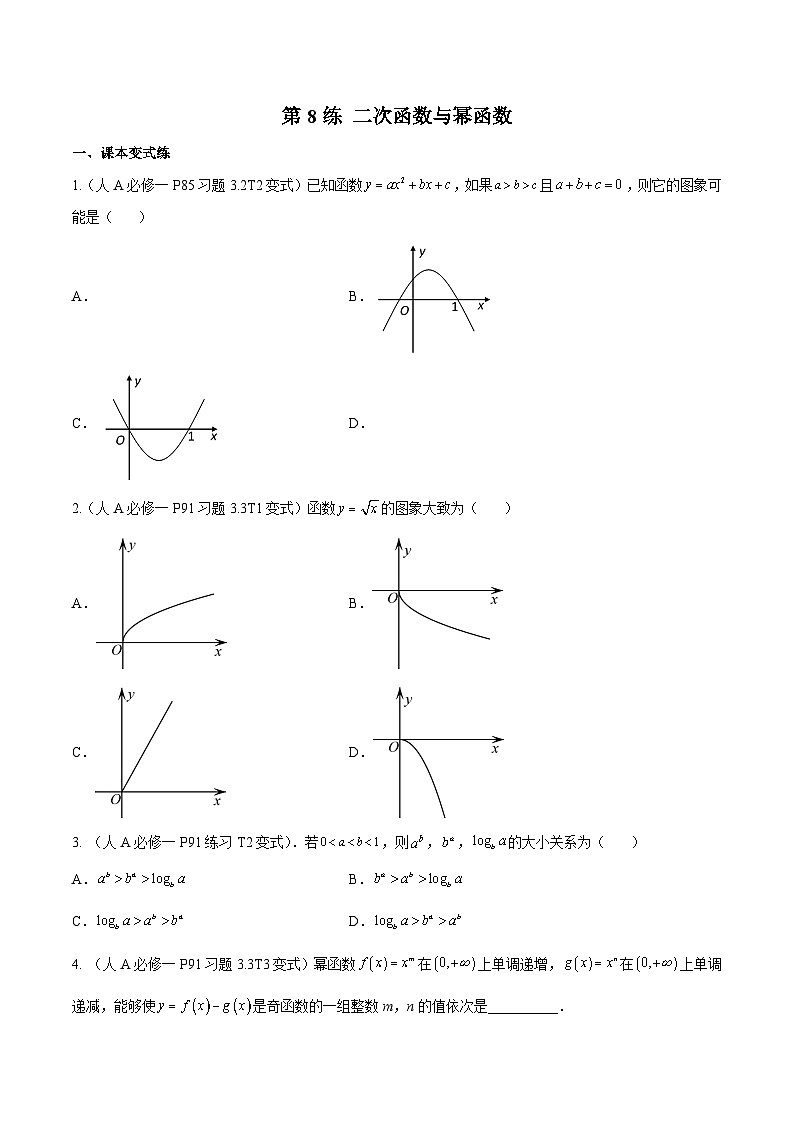
1.（人A必修一P85习题3.2T2变式）已知函数，如果且，则它的图象可能是（ ）
A．B．
C．D．
2.（人A必修一P91习题3.3T1变式）函数的图象大致为（ ）
A．B．
C．D．
3. （人A必修一P91练习T2变式）．若，则，，的大小关系为（ ）
A．B．
C．D．
4. （人A必修一P91习题3.3T3变式）幂函数在上单调递增，在上单调递减，能够使是奇函数的一组整数m，n的值依次是__________．
二、考点分类练
(一)幂函数的图象与性质
5.（2022届北京市第四中学高三下学期阶段性测试）下列函数的图象中，既是轴对称图形又是中心对称的是（ ）
A．B．
C．D．
6.“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
7．三个数，，的大小顺序是（ ）
A．>>B．>>
C．>>D．>>
8.（多选）（2022届广东省茂名市重点高中高三上学期段考）已知函数，则（ ）
A．函数过点（1，-1）.
B．若函数过（-1，1），函数为偶函数.
C．若函数过（-1，-1），函数为奇函数.
D．当时，使得函数.
9.（2022届山东省济宁市高三上学期月考）已知幂函数在为增函数，则实数的值为___________.
(二)二次函数的解析式、图象与性质
10．（2022届江西省九校高三上学期期中联考）若函数在是增函数，则的取值范围是（ ）
A．B．C．D．
11.（2022届北京市高三统一考试）已知函数，，则（ ）
A．最大值为2，最小值为1
B．最大值为，最小值为1
C．最大值为，最小值为1
D．最大值为，最小值为
12.（2022届山东省济南市高三上学期模拟）若二次函数，满足，则下列不等式成立的是（ ）
A．B．
C．D．
13．（2022届广东省佛山市高三二模）设且，函数，若，则下列判断正确的是（ ）
A．的最大值为-aB．的最小值为-a
C．D．
14．（2022届江西省上饶市六校高三第一次联考）函数在区间（－∞，2）上单调递增，则实数a的取值范围（ ）
A．B．C．D．
15. （2022届广东省肇庆市高三下学期质量检测）已知函数，，用表示m，n中的最小值，设函数，若恰有3个零点，则实数a的取值范围是___________.
三、最新模拟练
16.（2022届四川省乐山市高三第一次调查）已知幂函数和，其中，则有下列说法：
①和图象都过点；
②和图象都过点；
③在区间上，增长速度更快的是；
④在区间上，增长速度更快的是.
则其中正确命题的序号是（ ）
A．①③B．②③C．①④D．②④
17．（2022届百校大联考高三3月试题）已知函数，其中，，，则（ ）
A．，都有B．，都有
C．，使得D．，使得
18．（2022届四川省绵阳高三上学期月考）幂函数在上单调递增，则的图象过定点（ ）
A．B．C．D．
19.（2022届河南省开封市高三下学期核心模拟）已知函数满足对任意的实数，且，都有成立，则实数的取值范围为（ ）
A．B．
C．D．
20.(多选)设，，为正实数，且，则下列关系式可能成立的是（ ）
A．B．C．D．
21.（多选）（2022届广东省潮州市高三下学期二模）已知幂函数的图象经过点，则下列命题正确的有（ ）．
A．函数的定义域为
B．函数为非奇非偶函数
C．过点且与图象相切的直线方程为
D．若，则
22.（2022届北京市东城区高三模拟）某公司通过统计分析发现，工人工作效率E与工作年限，劳累程度，劳动动机相关，并建立了数学模型．
已知甲、乙为该公司的员工，给出下列四个结论：
①甲与乙劳动动机相同，且甲比乙工作年限长，劳累程度弱，则甲比乙工作效率高；
@甲与乙劳累程度相同，且甲比乙工作年限长，劳动动机高，则甲比乙工作效率高；
③甲与乙工作年限相同，且甲比乙工作效率高，劳动动机低，则甲比乙劳累程度强：
④甲与乙劳动动机相同，且甲比乙工作效率高，工作年限短．则甲比乙劳累程度弱．
其中所有正确结论的序号是__________．
四、高考真题练
23.(2021全国卷甲)设函数的定义域为R，为奇函数，为偶函数，当时，
．若，则( )
A．B．C．D．
24． (2016全国卷Ⅲ)已知,,,则( )
A．B．C．D．
25.(2016全国卷Ⅱ卷)已知函数满足，若函数与图像的
交点为，则( )
A．B．C．D．
五、综合提升练
26.设函数.若对任意的正实数和实数，总存在，使得，则实数的取值范围是（ ）
A．B．C．D．
27.已知函数，若在上单调递增，则的范围是（ ）
A．B．C．D．
28.（多选）（2022届江苏省泰州市兴化市高三下学期4月模拟）设一组样本的统计数据为：，其中n∈N*，．已知该样本的统计数据的平均数为，方差为，设函数，x∈R．则下列说法正确的是（ ）
A．设b∈R，则的平均数为
B．设a∈R，则的方差为
C．当x＝时，函数有最小值
D．
29.（2022届重庆市缙云教育联盟高三第二次诊断）关于x的不等式，解集为___________.
30.（2022届湖南省长沙市高三1月适应性考试）已知函数，，a为常数.若对于任意x1，x2∈[0，2]，且x1＜x2，都有，则实数a的取值范围是___________.
第8练 二次函数与幂函数
一、课本变式练
1.（人A必修一P85习题3.2T2变式）已知函数，如果且，则它的图象可能是（ ）
A．B．
C．D．
【答案】A
【解析】由题意，函数，因为，令，可得，即函数图象过点，
又由，可得，所以抛物线的开口向上，可排除D项，
令，可得，可排除B、C项；故选A.
2.（人A必修一P91习题3.3T1变式）函数的图象大致为（ ）
A．B．
C．D．
【答案】A
【解析】由，排除B、D，根据对应幂函数的性质，第一象限增速逐渐变慢，排除C.故选A.
3. （人A必修一P91练习T2变式）．若，则，，的大小关系为（ ）
A．B．
C．D．
【答案】D
【解析】因为，所以，因为，
所以．故选D．
4. （人A必修一P91习题3.3T3变式）幂函数在上单调递增，在上单调递减，能够使是奇函数的一组整数m，n的值依次是__________．
【答案】1，（答案不唯一）
【解析】因为幂函数在上单调递增，所以，因为幂函数在上单调递减，所以，又因为是奇函数，所以幂函数和幂函数都是奇函数，所以可以是，可以是.故答案为：1，（答案不唯一）.
二、考点分类练
(一)幂函数的图象与性质
5.（2022届北京市第四中学高三下学期阶段性测试）下列函数的图象中，既是轴对称图形又是中心对称的是（ ）
A．B．
C．D．
【答案】A
【解析】对于A，图象关于、坐标原点分别成轴对称和中心对称，A正确；
对于B，为偶函数，其图象关于轴对称，但无对称中心，B错误；
对于C，关于点成中心对称，但无对称轴，C错误；
对于D，为奇函数，其图象关于坐标原点成中心对称，但无对称轴，D错误.
故选A.
6.“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【解析】因为定义域为，且为增函数，又，所以，解得：，因为，而，故“”是“”的充分不必要条件.故选A
7．三个数，，的大小顺序是（ ）
A．>>B．>>
C．>>D．>>
【答案】C
【解析】由函数在上单调递增，则又由于在上单调递减，则
故，故选C
8.（多选）（2022届广东省茂名市重点高中高三上学期段考）已知函数，则（ ）
A．函数过点（1，-1）.
B．若函数过（-1，1），函数为偶函数.
C．若函数过（-1，-1），函数为奇函数.
D．当时，使得函数.
【答案】BC
【解析】，则，故A错误；函数过（-1，1），则，，即函数偶函数，B正确；若过（-1，-1），则，，即函数为奇函数，C正确；当时，在上单调递增，故，D错误.故选BC.
9.（2022届山东省济宁市高三上学期月考）已知幂函数在为增函数，则实数的值为___________.
【答案】4
【解析】为递增的幂函数，所以，即，解得
(二)二次函数的解析式、图象与性质
10．（2022届江西省九校高三上学期期中联考）若函数在是增函数，则的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】∵函数在是增函数∴，即，∴的取值范围是
故选B.
11.（2022届北京市高三统一考试）已知函数，，则（ ）
A．最大值为2，最小值为1
B．最大值为，最小值为1
C．最大值为，最小值为1
D．最大值为，最小值为
【答案】B
【解析】，
时，sinx∈[，1]，
∴当sinx＝时，f(x)最大值为；当sinx＝1时，f(x)最小值为1.
故选B.
12.（2022届山东省济南市高三上学期模拟）若二次函数，满足，则下列不等式成立的是（ ）
A．B．
C．D．
【答案】B
【解析】因为，所以二次函数的对称轴为，又因为，所以，又，所以.故选B.
13．（2022届广东省佛山市高三二模）设且，函数，若，则下列判断正确的是（ ）
A．的最大值为-aB．的最小值为-a
C．D．
【答案】D
【解析】依题意，，
因，则是奇函数，于是得，即，
因此，，而，当时，的最小值为-a，当时，的最大值为-a，A，B都不正确；
，，，
即，，因此，C不正确，D正确.故选D
14．（2022届江西省上饶市六校高三第一次联考）函数在区间（－∞，2）上单调递增，则实数a的取值范围（ ）
A．B．C．D．
【答案】B
【解析】由题设，，且各区间上对应的二次函数的对称轴均为，
又时不合题设，所以.
当时，在上开口向下，即上递增，上递减；当上开口向上，即上递增；
当时，在上开口向上，即上递减；当上开口向下，即上递增，上递减；
综上，要使在（－∞，2）上单调递增，有，可得.故选B.
15. （2022届广东省肇庆市高三下学期质量检测）已知函数，，用表示m，n中的最小值，设函数，若恰有3个零点，则实数a的取值范围是___________.
【答案】
【解析】函数恒过点 ，且其图象开口向上，的零点为1，
当的零点至少有一个大于或等于1时，如图示：
函数的零点至多有两个，不符合题意，
故要使恰有3个零点，则函数在区间上存在两个零点，如图示，
故
解得，
三、最新模拟练
16.（2022届四川省乐山市高三第一次调查）已知幂函数和，其中，则有下列说法：
①和图象都过点；
②和图象都过点；
③在区间上，增长速度更快的是；
④在区间上，增长速度更快的是.
则其中正确命题的序号是（ ）
A．①③B．②③C．①④D．②④
【答案】A
【解析】幂函数的图象过定点，①正确，在区间上，越大增长速度更快，③正确，
故选A.
17．（2022届百校大联考高三3月试题）已知函数，其中，，，则（ ）
A．，都有B．，都有
C．，使得D．，使得
【答案】B
【解析】由，，可知，，抛物线开口向上．因为，，即1是方程的一个根，所以，都有，B正确，A、C、D错误.故选B．
18．（2022届四川省绵阳高三上学期月考）幂函数在上单调递增，则的图象过定点（ ）
A．B．C．D．
【答案】D
【解析】因为幂函数在上单调递增，所以，解得，所以，故令得，所以，所以的图象过定点，故选D
19.（2022届河南省开封市高三下学期核心模拟）已知函数满足对任意的实数，且，都有成立，则实数的取值范围为（ ）
A．B．
C．D．
【答案】D
【解析】因为对任意的实数，且，都有成立，
所以，对任意的实数，且，，即函数是上的减函数．
因为，
令，，要使在上单调递减，所以，在上单调递增．另一方面，函数为减函数，所以，，解得，
所以实数a的取值范围是．故选D．
20.(多选)设，，为正实数，且，则下列关系式可能成立的是（ ）
A．B．C．D．
【答案】ACD
【解析】，即
令，则，当时，当时，因为幂函数在上单调递增，，，当时，因为幂函数在上单调递减，，.故选ACD.
21.（多选）（2022届广东省潮州市高三下学期二模）已知幂函数的图象经过点，则下列命题正确的有（ ）．
A．函数的定义域为
B．函数为非奇非偶函数
C．过点且与图象相切的直线方程为
D．若，则
【答案】BC
【解析】设，将点代入，得，则，即，
对于A：的定义域为，即选项A错误；对于B：因为的定义域为，
所以不具有奇偶性，即选项B正确；对于C：因为，所以，
设切点坐标为，则切线斜率为，切线方程为，又因为切线过点，所以，解得，即切线方程为，即，
即选项C正确；对于D：当时，
，
即成立，即选项D错误．故选BC．
22.（2022届北京市东城区高三模拟）某公司通过统计分析发现，工人工作效率E与工作年限，劳累程度，劳动动机相关，并建立了数学模型．
已知甲、乙为该公司的员工，给出下列四个结论：
①甲与乙劳动动机相同，且甲比乙工作年限长，劳累程度弱，则甲比乙工作效率高；
@甲与乙劳累程度相同，且甲比乙工作年限长，劳动动机高，则甲比乙工作效率高；
③甲与乙工作年限相同，且甲比乙工作效率高，劳动动机低，则甲比乙劳累程度强：
④甲与乙劳动动机相同，且甲比乙工作效率高，工作年限短．则甲比乙劳累程度弱．
其中所有正确结论的序号是__________．
【答案】①②④
【解析】设甲与乙的工人工作效率，工作年限，劳累程度，劳动动机，
对于①，，，，，，∴，，
则，
∴，即甲比乙工作效率高，故①正确；对于②，，，，
∴，，
则，
∴，即甲比乙工作效率高，故②正确；
对于③，，，，，
∴，，
，
所以，即甲比乙劳累程度弱，故③错误；
对于④，，，，
∴，，
∴，
所以，即甲比乙劳累程度弱，故④正确.
故答案为①②④.
四、高考真题练
23.(2021全国卷甲)设函数的定义域为R，为奇函数，为偶函数，当时，
．若，则( )
A．B．C．D．
【答案】D
【解析】因为是奇函数，所以①；
因为是偶函数，所以②．
令，由①得：，由②得：，
因为，所以，
令，由①得：，所以．
所以．
24． (2016全国卷Ⅲ)已知,,,则( )
A．B．C．D．
【答案】A
【解析】因为,,故选A.
25.(2016全国卷Ⅱ卷)已知函数满足，若函数与图像的
交点为，则( )
A．B．C．D．
【答案】B
【解析】的图像的对称中心为
又函数满足，所以图像的对称中心为：
所以，故选Ｂ
五、综合提升练
26.设函数.若对任意的正实数和实数，总存在，使得，则实数的取值范围是（ ）
A．B．C．D．
【答案】B
【解析】设的最大值为，令，当时，函数单调递减，，，
由，解得
由，时，；时，；时
由，，
由时，，，
综上可得：，
27.已知函数，若在上单调递增，则的范围是（ ）
A．B．C．D．
【答案】D
【解析】,
若在上单调递增
则在恒成立,
令则,又故, ,所以问题转化为不等式在上恒成立，即不等式在上恒成立.令, ,则有,解得.
故选.
28.（多选）（2022届江苏省泰州市兴化市高三下学期4月模拟）设一组样本的统计数据为：，其中n∈N*，．已知该样本的统计数据的平均数为，方差为，设函数，x∈R．则下列说法正确的是（ ）
A．设b∈R，则的平均数为
B．设a∈R，则的方差为
C．当x＝时，函数有最小值
D．
【答案】AC
【解析】对于A，的平均数，的平均数为，正确；
对于B，的方差，的平均数为，方差为，错误；
对于C，，又，，故，故当x＝时，函数有最小值，正确；对于D，由上知，，错误.故选AC.
29.（2022届重庆市缙云教育联盟高三第二次诊断）关于x的不等式，解集为___________.
【答案】
【解析】由题设，，而在R上递增，
当即时，，原不等式不成立；
当即时，，原不等式恒成立.
综上，解集为.
30.（2022届湖南省长沙市高三1月适应性考试）已知函数，，a为常数.若对于任意x1，x2∈[0，2]，且x1＜x2，都有，则实数a的取值范围是___________.
【答案】[0，1]
【解析】对于任意x1，x2∈[0，2]，且x1＜x2，都有，即，令，即只需在[0，2]上单调递增即可，
当时，，函数图象恒过；
当时，；
当时，；
要使在区间[0，2]上单调递增，则当时，的对称轴
，即；
当时，的对称轴，即；
且,综上