

北师大版八年级数学下册压轴题攻略期末考试B卷压轴题模拟训练(三)(原卷版+解析)
展开19.已知a=b﹣2,则代数式的值为_____.
20.不等式组的解集是x≤3,那么a的取值范围_____.
21.若一次函数的图象经过第一,三,四象限,且关于的分式方程的解为非负数,则满足条件的取值范围为_________.
22.如图,已知四边形ABCD是平行四边形,将边AD绕点D逆时针旋转60°得到DE,线段DE交边BC于点F,连接BE.若∠C+∠E=150°,BE=2,CD=2,则线段BC的长为_____.
23.如图,在中,,,于点D,平分交于点E,交于点G,过点A作于点H,交于点F,下列结论:①;②;③;④,其中正确的序号有______.
二、解答题
24.沙坪坝区2017年已经成功创建国家卫生城区,现在正全力争创全国文明城区(简称“创文”),某街道积极响应“创文”活动,投入一定资金用于绿化一块闲置空地,购买了甲、乙两种树木共72棵,其中甲种树木每棵90元,乙种树木每棵80元,共用去资金6160元.
(1)求甲、乙两种树木各购买了多少棵?
(2)经过一段时间后,种植的这批树木成活率高,绿化效果好,该街道决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了,乙种树木单价下降了,且总费用不超过6804元,求的最大值.
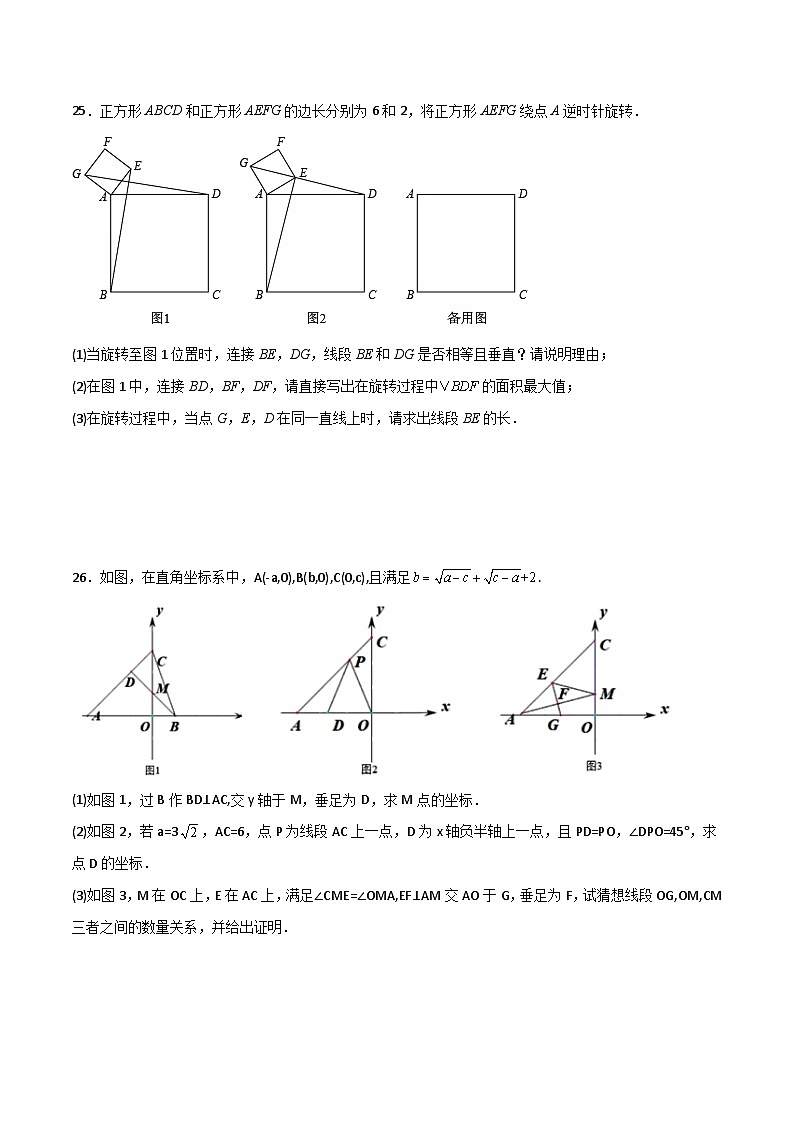
25.正方形ABCD和正方形AEFG的边长分别为6和2,将正方形AEFG绕点A逆时针旋转.
(1)当旋转至图1位置时,连接BE,DG,线段BE和DG是否相等且垂直?请说明理由;
(2)在图1中,连接BD,BF,DF,请直接写出在旋转过程中的面积最大值;
(3)在旋转过程中,当点G,E,D在同一直线上时,请求出线段BE的长.
26.如图,在直角坐标系中,A(-a,0),B(b,0),C(0,c),且满足.
(1)如图1,过B作BD⊥AC,交y轴于M,垂足为D,求M点的坐标.
(2)如图2,若a=3,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
(3)如图3,M在OC上,E在AC上,满足∠CME=∠OMA,EF⊥AM交AO于G,垂足为F,试猜想线段OG,OM,CM三者之间的数量关系,并给出证明.
期末考试B卷压轴题模拟训练(三)
一、填空题
19.已知a=b﹣2,则代数式的值为_____.
【答案】12
【分析】由已知等式得出,代入到原式计算可得答案.
【详解】解:,
故答案为:12.
【点睛】本题主要考查了完全平方的运算,其中熟练掌握完全平方公式是解题的关键.
20.不等式组的解集是x≤3,那么a的取值范围_____.
【答案】a>1
【分析】先求出两个不等式的解集,再求其公共解,然后根据不等式的同小取小列出不等式,然后求解即可.
【详解】解:,
解不等式②得,x≤3,
∵不等式组的解集是x≤3,
∴2a+1>3,
解得a>1,
∴a的取值范围a>1.
故答案为a>1.
【点睛】本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).
21.若一次函数的图象经过第一,三,四象限,且关于的分式方程的解为非负数,则满足条件的取值范围为_________.
【答案】且
【分析】根据一次函数经过第一、三、四象限则得到;再解分式方程得到,结合分式方程解得情况求解即可.
【详解】解:∵一次函数的图象经过第一,三,四象限,
∴,解得;
去分母得:,去括号得:,∴,
∵关于的分式方程的解为非负数,∴,解得且,
综上所述,且,
故答案为:且.
【点睛】本题主要考查了一次函数图象与系数的关系,根据分式方程解的情况求参数,解一元一次不等式组,灵活运用所学知识是解题的关键.
22.如图,已知四边形ABCD是平行四边形,将边AD绕点D逆时针旋转60°得到DE,线段DE交边BC于点F,连接BE.若∠C+∠E=150°,BE=2,CD=2,则线段BC的长为_____.
【答案】2
【分析】过C作CM⊥DE于M,过E作EN⊥BC于N,根据平行四边形的性质得到BC∥AD,根据平行线的性质得到∠BFE=∠DFC=∠ADE,根据旋转的性质得到∠BFE=∠DFC=∠ADE=60°,推出∠DCM=∠EBN,根据相似三角形的性质得到CM=BN,DM=EN,得到FM=BN,设FM=BN=x,EN=y,则DM=y,CM=x,根据勾股定理即可得到结论.
【详解】解:过C作CM⊥DE于M,过E作EN⊥BC于N,
∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠BFE=∠DFC=∠ADE,
∵将边AD绕点D逆时针旋转60°得到DE,
∴∠BFE=∠DFC=∠ADE=60°,
∴∠FCM=∠FBN=30°,
∵∠DCF+∠BEF=150°,
∴∠DCM+∠BEN=90°,
∵∠BEN+∠EBN=90°,
∴∠DCM=∠EBN,
∴==,
∴CM=BN,DM=EN,
在Rt△CMF中,CM=FM,
∴FM=BN,
设FM=BN=x,EN=y,则DM=y,CM=x,
∴CF=2x,EF=y,
∵BC=AD=DE,
∴y+x+y=2x+y+x,∴x=y,
∵x2+y2=4,
∴y=,x=,
∴BC=2,
故答案为:2.
【点评】本题考查了平行四边形的性质,相似三角形的判定和性质,勾股定理,旋转的性质,正确的作出辅助线是解题的关键.
23.如图,在中,,,于点D,平分交于点E,交于点G,过点A作于点H,交于点F,下列结论:①;②;③;④,其中正确的序号有______.
【答案】①③④
【分析】根据角平分线定义得到,根据余角的性质得到,等量代换得到,故①正确;如图,连接,根据全等三角形的性质得到,根据线段垂直平分线的性质得到,求得,故②错误;根据全等三角形的性质得到,根据等腰直角三角形的性质得到,求得,故③正确;根据全等三角形的性质得到,推出,得到,于是得到.故④正确.
【详解】解:∵平分交于点E,
∴,
∵,
∴,
∴,
∴,
∵,
∴,故①正确;
如图,连接,
∵,,,
∴,
∴,
∴垂直平分,
∴,
∴,
∵,
∴,
∴,
∴,故②错误;
∵垂直平分,
∴,
∴,
∴,
∴是等腰直角三角形,
∴,
∵,
∴,故③正确;
∵,,
∴,
∵,,
∴,
∴,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴,
∴.故④正确;
综上所述:正确的是①③④.
故答案为:①③④.
【点睛】本题是三角形的综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,线段垂直平分线的性质,熟练掌握全等三角形的性质和判定定理是解题的关键.
二、解答题
24.沙坪坝区2017年已经成功创建国家卫生城区,现在正全力争创全国文明城区(简称“创文”),某街道积极响应“创文”活动,投入一定资金用于绿化一块闲置空地,购买了甲、乙两种树木共72棵,其中甲种树木每棵90元,乙种树木每棵80元,共用去资金6160元.
(1)求甲、乙两种树木各购买了多少棵?
(2)经过一段时间后,种植的这批树木成活率高,绿化效果好,该街道决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了,乙种树木单价下降了,且总费用不超过6804元,求的最大值.
【答案】(1)甲种40棵,乙种32棵,(2)25.
【分析】(1)设甲种树苗购买了棵,乙种树苗购买了棵,根据总费用单价数量结合“购买了甲、乙两种树木共72棵,共用去资金6160元”,即可得出关于,的二元一次方程组,解之即可得出结论;
(2)根据总费用单价数量结合总费用不超过6804元,即可得出关于的一元一次不等式,解之取其中的最大值即可得出结论.
【详解】解:(1)设甲种树苗购买了棵,乙种树苗购买了棵,
根据题意得:,
解得:.
答:甲种树苗购买了40棵,乙种树苗购买了32棵.
(2)根据题意得:,
解得:.
答:的最大值为25.
【点睛】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
25.正方形ABCD和正方形AEFG的边长分别为6和2,将正方形AEFG绕点A逆时针旋转.
(1)当旋转至图1位置时,连接BE,DG,线段BE和DG是否相等且垂直?请说明理由;
(2)在图1中,连接BD,BF,DF,请直接写出在旋转过程中的面积最大值;
(3)在旋转过程中,当点G,E,D在同一直线上时,请求出线段BE的长.
【答案】(1)相等且垂直,理由见解析
(2)30
(3)BE的长为或
【分析】(1)如图,证明,可得结论;
(2)如图,取的中点,连接、、,过点作于点,根据三角形的三边关系,推出的最大值,由此可得结论;
(3)分两种情形:如图,当点在线段上时.如图当点在线段的延长线上时,利用勾股定理即可得出结论.
【详解】(1)解:(1)数量关系:,位置关系:,
理由如下:如图,设 与交于点,连接,
∵四边形、四边形都是正方形,
∴,,,
∴即,
在和中,
,
,
,,
,
即,
,
故与的数量关系为:,位置关系为:;
(2)解:如图,取的中点,连接、、,过点作于点,
,为中点,,
,
,
,
四边形是正方形,
,
,
即的最大值为,
,
当最大时,的面积也最大,
面积的最大值为;
(3)解:当点在线段上时,如图,连接交于点,
四边形是正方形,
,,
在中,由勾股定理得,
,
,
当点在线段的延长线上时,如图,连接交于点,
同理可得:,
在中,由勾股定理得,
,
,
综上所述,的长为或.
【点睛】本题属于四边形综合题,考查了正方形的性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题,学会用分类讨论的思想思考问题.
26.如图,在直角坐标系中,A(-a,0),B(b,0),C(0,c),且满足.
(1)如图1,过B作BD⊥AC,交y轴于M,垂足为D,求M点的坐标.
(2)如图2,若a=3,AC=6,点P为线段AC上一点,D为x轴负半轴上一点,且PD=PO,∠DPO=45°,求点D的坐标.
(3)如图3,M在OC上,E在AC上,满足∠CME=∠OMA,EF⊥AM交AO于G,垂足为F,试猜想线段OG,OM,CM三者之间的数量关系,并给出证明.
【答案】(1)M(0,2);(2)D(,0);(3)OG+OM=CM,证明见解析.
【分析】(1)由被开方数大于等于0,可得a=c,b=2,则B点坐标为(2,0),易得△OAC和△OBM为等腰直角三角形,所以OM=OB=2,从而得到M点坐标;
(2)由“一线三等角”模型,易证△PAD≌△OCP,从而得到AP=OC,AD=PC,即可求出OD的长度,进而得到D点坐标;
(3)设OM=m,则M点坐标为(0,m),分别求出AC、AM、EM的解析式,将EM与AC联立求得E点坐标,再根据EF⊥AM,可得EF的斜率,进而求出EF的解析式,然后求出G点坐标即可得出关系.
【详解】解:(1)由题意得,
∴,
∴OA=OC,B点坐标(2,0)
∴∠OAC=∠OCA=45°,
又∵BD⊥AC
∴∠OBM=45°,
∴∠OMB=∠OBM=45°,
∴OM=OB=2
∴M点的坐标为(0,2)
(2)∵∠APO=∠APD+∠DPO=∠PCO+∠POC,且∠DPO=∠PCO=45°
∴∠APD=∠POC
在△PAD和△OCP中,
∴△PAD≌△OCP(AAS)
∴AP=OC=,AD=PC
∴PC=AC-AP==AD
∴OD=OA-AD=
∵D点在x轴负半轴,
∴D点坐标为(,0)
(3)OG+OM=CM,证明如下:
设OM=m,则M点坐标为(0,m)
由(1)可知OA=OC=a,A点坐标为(-a,0),C点坐标为(0,a)
∴AC直线解析式为:
AM直线解析式为:
如图,延长EM,AO交于点H,
∵∠CME=∠OMA,∠CME=∠OMH
∴∠OMA=∠OMH
又∵MO⊥AH
∴OA=OH=a
∴直线EH解析式为:
将直线AC与直线EH联立得
解得
∴E点坐标为(,)
∵EF⊥AM
∴kEF·kAM=-1
∴kEF=
设EF解析式为:
将E点坐标(,)代入得
=,解得
设EF解析式为:
当y=0时,
解得
∴G点坐标为(,0)
∵G在x轴的负半轴
∴OG=
∴OG+OM=
又∵CM=OC-OM=
∴OG+OM=CM
【点睛】本题考查了坐标系中的几何问题,熟练掌握几何模型,以及一次函数的图像与性质,是解决本题的关键,难度较大,需要综合运用所学知识.
北师大版八年级数学下册压轴题攻略期末考试点对点压轴题训练(五)(B卷26题)(原卷版+解析): 这是一份北师大版八年级数学下册压轴题攻略期末考试点对点压轴题训练(五)(B卷26题)(原卷版+解析),共42页。试卷主要包含了【数学初探】,已知为等边三角形,其边长为,证明见解答等内容,欢迎下载使用。
北师大版八年级数学下册压轴题攻略期末考试点对点压轴题训练(四)(B卷25题)(原卷版+解析): 这是一份北师大版八年级数学下册压轴题攻略期末考试点对点压轴题训练(四)(B卷25题)(原卷版+解析),共50页。试卷主要包含了在平面直角坐标系中,直线l1,平面直角坐标系中,直线,直线,由所作辅助线可知,,等内容,欢迎下载使用。
期末考试B卷压轴题模拟训练(三)-【B卷常考】2022-2023学年七年级数学下册压轴题攻略: 这是一份期末考试B卷压轴题模拟训练(三)-【B卷常考】2022-2023学年七年级数学下册压轴题攻略,文件包含期末考试B卷压轴题模拟训练三原卷版docx、期末考试B卷压轴题模拟训练三解析版docx等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。












