


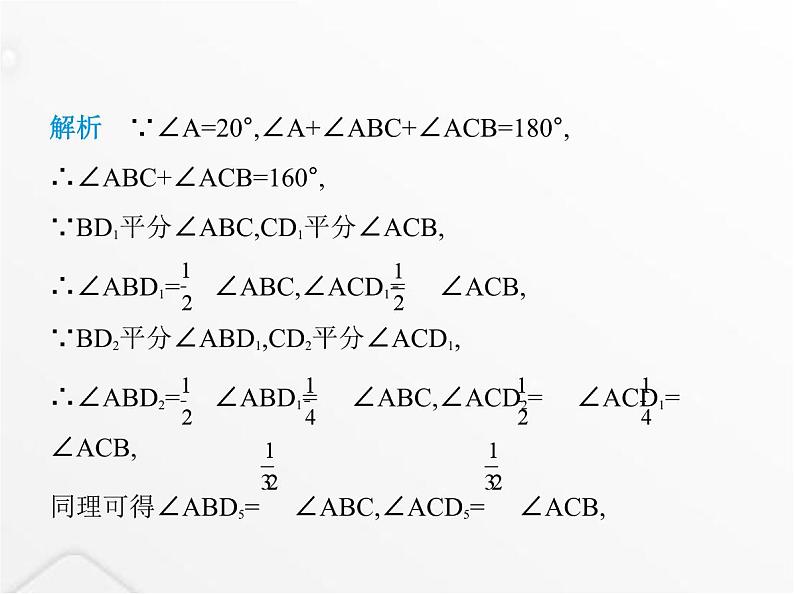

还剩8页未读,
继续阅读
所属成套资源:全套北师大版初中八年级数学上册专项素养综合练课件
成套系列资料,整套一键下载
北师大版初中八年级数学上册专项素养综合练(八)四种常见的角平分线模型课件
展开
这是一份北师大版初中八年级数学上册专项素养综合练(八)四种常见的角平分线模型课件,共15页。
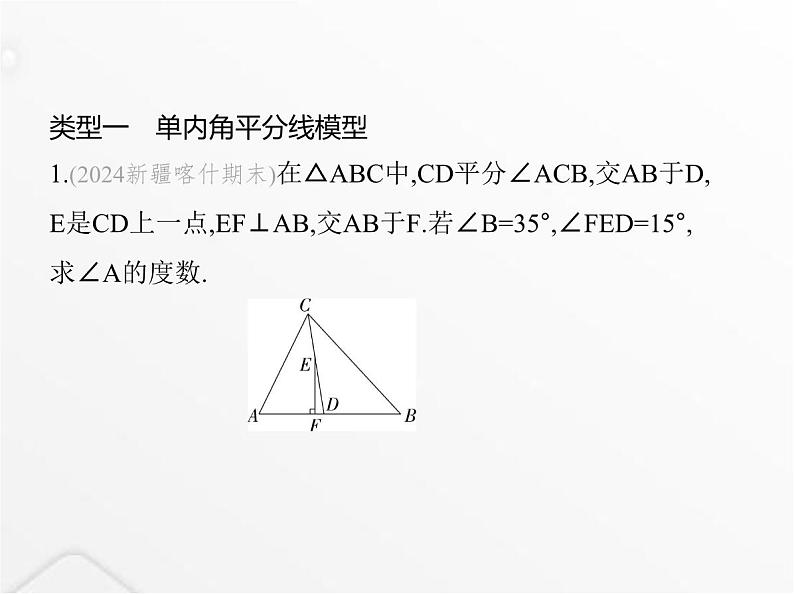
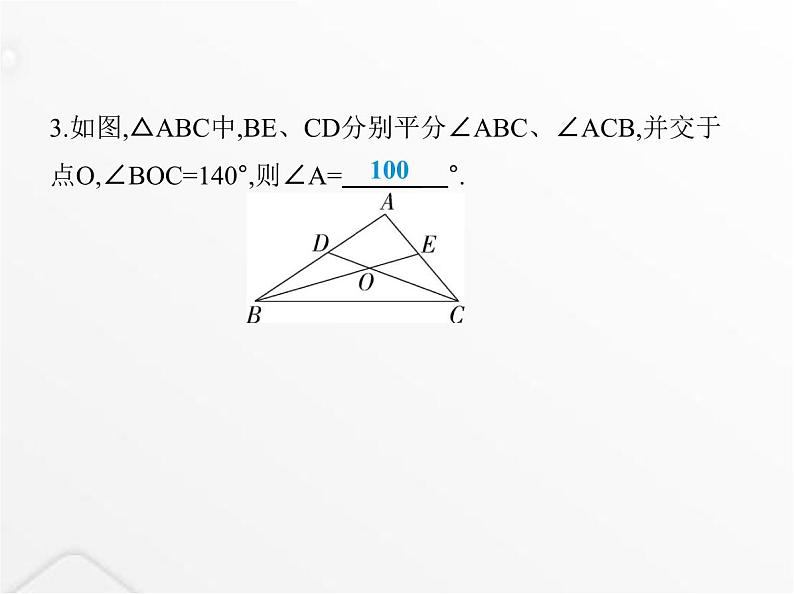
四种常见的角平分线模型专项素养综合全练(八)类型一 单内角平分线模型1.(2024新疆喀什期末)在△ABC中,CD平分∠ACB,交AB于D,E是CD上一点,EF⊥AB,交AB于F.若∠B=35°,∠FED=15°,求∠A的度数. 解析 ∵EF⊥AB,∴∠EFB=90°,∵∠FED=15°,∴∠EDF=90°-∠FED=75°.∵∠EDF是△BCD的一个外角,∴∠BCD=∠EDF-∠B=75°-35°=40°.∵CD平分∠ACB,∴∠ACB=2∠BCD=80°,∴∠A=180°-∠B-∠ACB=65°.类型二 双内角平分线模型2.如图,在△ABC中,若∠A=20°,∠ABC与∠ACB的平分线交 于D1,∠ABD1与∠ACD1的平分线交于点D2,依此类推,∠ABD4与∠ACD4的平分线交于点D5,则∠BD5C的度数是( )A.24° B.25° C.30° D.36° B解析 ∵∠A=20°,∠A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=160°,∵BD1平分∠ABC,CD1平分∠ACB,∴∠ABD1= ∠ABC,∠ACD1= ∠ACB,∵BD2平分∠ABD1,CD2平分∠ACD1,∴∠ABD2= ∠ABD1= ∠ABC,∠ACD2= ∠ACD1= ∠ACB,同理可得∠ABD5= ∠ABC,∠ACD5= ∠ACB,∴∠ABD5+∠ACD5= ×160°=5°,∴∠BCD5+∠CBD5=155°,∴∠BD5C=180°-∠BCD5-∠CBD5=25°.故选B.3.如图,△ABC中,BE、CD分别平分∠ABC、∠ACB,并交于 点O,∠BOC=140°,则∠A= °. 100解析 如图, ∵BO平分∠ABC,CO平分∠ACB,∴∠ABC=2∠1,∠ACB=2∠2,∵∠BOC=140°,∴∠1+∠2=180°-140°=40°,∴∠ABC+∠ACB=2×40°=80°,∴∠A=180°-80°=100°,故答案为100.类型三 内、外角平分线模型4.(2022重庆九龙坡校级月考)如图,在△ABC中,∠C=110°, AE是△ABC的外角∠BAD的平分线,BF平分∠ABC,与AE的 反向延长线交于点F,则∠BFE的度数为 . 55°解析 ∵BF平分∠ABC,∴∠ABF= ∠ABC.∵AE平分∠DAB,∴∠EAB= ∠DAB.∵∠DAB-∠ABC=∠C=110°,∴∠EAB-∠ABF=55°,∴∠BFE=∠EAB-∠ABF=55°.5.如图.(1)思考探究:△ABC的内角∠ABC的平分线与外角∠ACD 的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数.(2)类比探究:△ABC的内角∠ABC的平分线与外角∠ACD 的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子 表示).解析 (1)∵∠ACD+∠ACB=180°,∠ACD=100°,∴∠ACB=80°,∵∠ABC=70°,∠ABC+∠ACB+∠A=180°(三角形内角和定 理),∴∠A=30°.∵P点是∠ABC和∠ACD的平分线的交点,∴∠PCD= ∠ACD=50°,∠PBC= ∠ABC=35°.∵∠PCD=∠PBC+∠P,∴∠P=50°-35°=15°.(2)结论:∠A=2n°,理由如下:∵P点是∠ABC和∠ACD的平分线的交点,∴∠ACD=2∠PCD,∠ABC=2∠PBC,∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC(三角形的一个 外角等于与它不相邻的两个内角和),∴∠A+∠ABC=∠ACD=2∠PCD=2(∠P+∠PBC)(等量代换),∴∠A+∠ABC=2∠P+2∠PBC,∴∠A+∠ABC=2∠P+∠ABC(等量代换),∴∠A=2∠P,∴∠A=2n°.类型四 双外角平分线模型6.(2023四川达州通川期末)如图所示,在△ABC中,∠B=47°, 三角形的外角∠DAC与∠ACF的平分线交于点E,则∠AEC= °. 66.5解析 如图.∵∠DAC和∠ACF的平分线交于点E,∴∠EAC= ∠DAC,∠ECA= ∠ACF,又∵∠B=47°,∠B+∠1+∠2=180°,∴ ∠DAC+ ∠ACF= (∠B+∠2)+ (∠B+∠1)= (∠B+∠B+∠1+∠2)=113.5°,∴∠AEC=180°- =66.5°.
四种常见的角平分线模型专项素养综合全练(八)类型一 单内角平分线模型1.(2024新疆喀什期末)在△ABC中,CD平分∠ACB,交AB于D,E是CD上一点,EF⊥AB,交AB于F.若∠B=35°,∠FED=15°,求∠A的度数. 解析 ∵EF⊥AB,∴∠EFB=90°,∵∠FED=15°,∴∠EDF=90°-∠FED=75°.∵∠EDF是△BCD的一个外角,∴∠BCD=∠EDF-∠B=75°-35°=40°.∵CD平分∠ACB,∴∠ACB=2∠BCD=80°,∴∠A=180°-∠B-∠ACB=65°.类型二 双内角平分线模型2.如图,在△ABC中,若∠A=20°,∠ABC与∠ACB的平分线交 于D1,∠ABD1与∠ACD1的平分线交于点D2,依此类推,∠ABD4与∠ACD4的平分线交于点D5,则∠BD5C的度数是( )A.24° B.25° C.30° D.36° B解析 ∵∠A=20°,∠A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=160°,∵BD1平分∠ABC,CD1平分∠ACB,∴∠ABD1= ∠ABC,∠ACD1= ∠ACB,∵BD2平分∠ABD1,CD2平分∠ACD1,∴∠ABD2= ∠ABD1= ∠ABC,∠ACD2= ∠ACD1= ∠ACB,同理可得∠ABD5= ∠ABC,∠ACD5= ∠ACB,∴∠ABD5+∠ACD5= ×160°=5°,∴∠BCD5+∠CBD5=155°,∴∠BD5C=180°-∠BCD5-∠CBD5=25°.故选B.3.如图,△ABC中,BE、CD分别平分∠ABC、∠ACB,并交于 点O,∠BOC=140°,则∠A= °. 100解析 如图, ∵BO平分∠ABC,CO平分∠ACB,∴∠ABC=2∠1,∠ACB=2∠2,∵∠BOC=140°,∴∠1+∠2=180°-140°=40°,∴∠ABC+∠ACB=2×40°=80°,∴∠A=180°-80°=100°,故答案为100.类型三 内、外角平分线模型4.(2022重庆九龙坡校级月考)如图,在△ABC中,∠C=110°, AE是△ABC的外角∠BAD的平分线,BF平分∠ABC,与AE的 反向延长线交于点F,则∠BFE的度数为 . 55°解析 ∵BF平分∠ABC,∴∠ABF= ∠ABC.∵AE平分∠DAB,∴∠EAB= ∠DAB.∵∠DAB-∠ABC=∠C=110°,∴∠EAB-∠ABF=55°,∴∠BFE=∠EAB-∠ABF=55°.5.如图.(1)思考探究:△ABC的内角∠ABC的平分线与外角∠ACD 的平分线相交于P点,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度数.(2)类比探究:△ABC的内角∠ABC的平分线与外角∠ACD 的平分线相交于P点,已知∠P=n°.求∠A的度数(用含n的式子 表示).解析 (1)∵∠ACD+∠ACB=180°,∠ACD=100°,∴∠ACB=80°,∵∠ABC=70°,∠ABC+∠ACB+∠A=180°(三角形内角和定 理),∴∠A=30°.∵P点是∠ABC和∠ACD的平分线的交点,∴∠PCD= ∠ACD=50°,∠PBC= ∠ABC=35°.∵∠PCD=∠PBC+∠P,∴∠P=50°-35°=15°.(2)结论:∠A=2n°,理由如下:∵P点是∠ABC和∠ACD的平分线的交点,∴∠ACD=2∠PCD,∠ABC=2∠PBC,∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC(三角形的一个 外角等于与它不相邻的两个内角和),∴∠A+∠ABC=∠ACD=2∠PCD=2(∠P+∠PBC)(等量代换),∴∠A+∠ABC=2∠P+2∠PBC,∴∠A+∠ABC=2∠P+∠ABC(等量代换),∴∠A=2∠P,∴∠A=2n°.类型四 双外角平分线模型6.(2023四川达州通川期末)如图所示,在△ABC中,∠B=47°, 三角形的外角∠DAC与∠ACF的平分线交于点E,则∠AEC= °. 66.5解析 如图.∵∠DAC和∠ACF的平分线交于点E,∴∠EAC= ∠DAC,∠ECA= ∠ACF,又∵∠B=47°,∠B+∠1+∠2=180°,∴ ∠DAC+ ∠ACF= (∠B+∠2)+ (∠B+∠1)= (∠B+∠B+∠1+∠2)=113.5°,∴∠AEC=180°- =66.5°.
相关资料
更多









